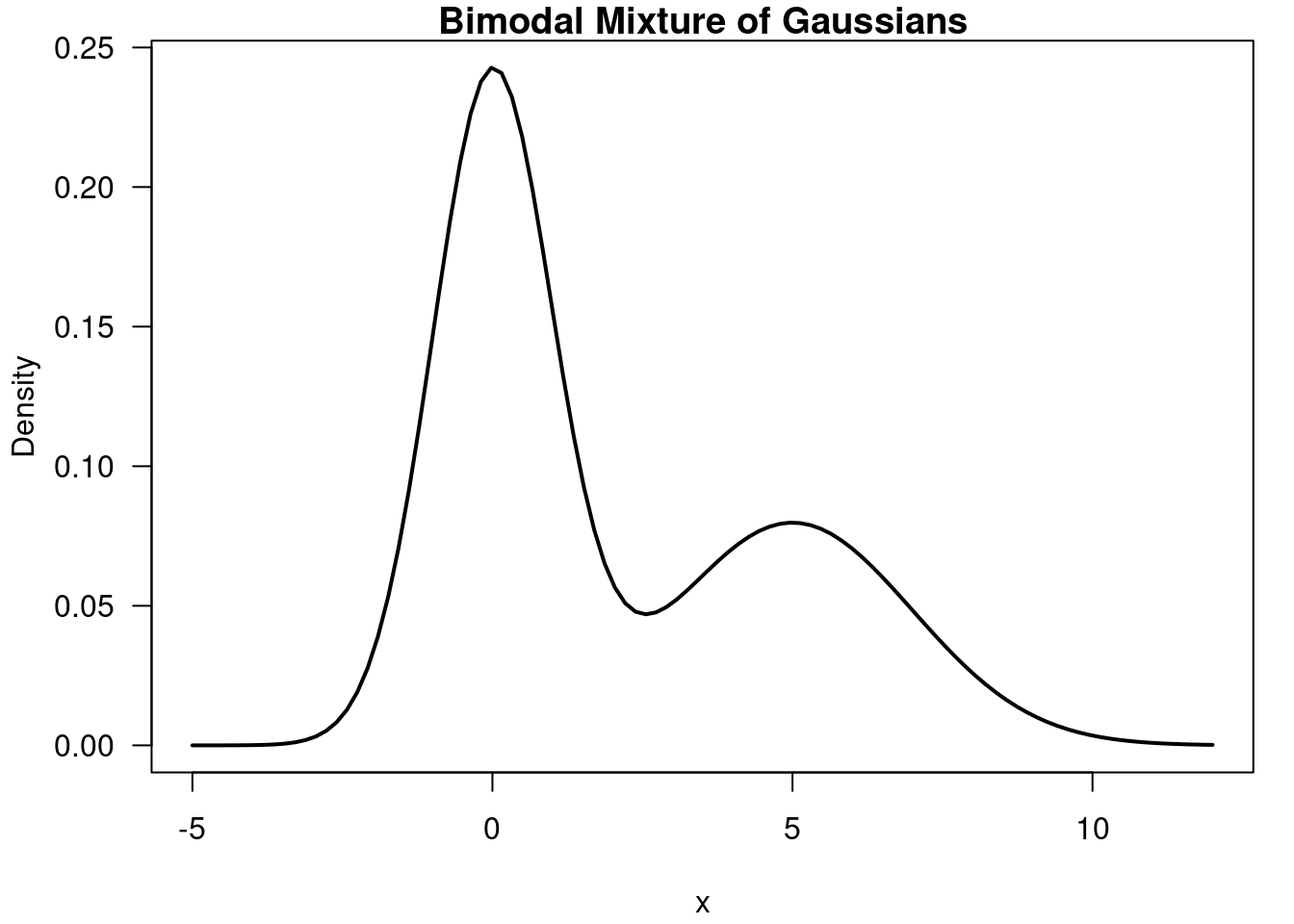
# Mixture of univariate Gaussians, bimodal
x = seq(-5, 12, length=100)
y = 0.6*dnorm(x, 0, 1) + 0.4*dnorm(x, 5, 2)
par(mar=c(4,4,1,1)+0.1)
plot(x, y, type="l", ylab="Density", las=1, lwd=2)
# set the title
title("Bimodal Mixture of Gaussians")This module titled “Basic concepts on Mixture Models” defines mixture models, discusses their properties, and develops the likelihood function for a random sample from a mixture model that will be the basis for statistical learning.
The module begins with a welcome section and a video and a reading on installing as well as a 103 page long handout titled “introduction to R”. I skipped this obligatory section as I this has already been adequately covered in the notes for the previous courses.
This handout: Mixture model are the instructor notes for this course.
55.1 Basic Definitions 🎥
Mixture models provide a flexible approach to modeling data. We will soon learn how mixtures may be utilized for density estimation Section 73.1, clustering Section 74.1 and classification Section 75.1 problems:
- Standard families of probability distributions like the Gaussian, exponential or Poisson may be too restrictive for modeling features of real data such as multimodality or zero inflation. Mixture models, which can be related to kernel density estimation procedures, address this issue in a way that allows for natural generalizations of well-known procedures.
- In addition to providing flexible probability distributions, finite mixture models have a strong relationship with classical clustering and classification procedures such as K-mean clustering, as well as linear and quadratic discriminant analysis. More generally they provide a tool to understand and generalize these approaches, as well as to quantify the uncertainty associated with the estimates and predictions generated by them.
55.2 Introduction to Mixture modeling 🎥
55.2.1 Definition of a finite mixture model
Definition 55.1 Let \omega_1 , \ldots , \omega_K be a collection of real numbers such that 0 \le \omega_k \le 1 and \sum^K_{k=1} \omega_k = 1, and G_1, \ldots, G_K be a collection of cumulative distribution functions. A random variable X with cumulative distribution function F(x) = Pr(X \le x) of the form:
F(x) =\sum^K_{k=1} \underbrace{\omega_k}_{weight}\ \cdot \ \underbrace{G_k(X)}_{component} \qquad \tag{55.1}
is said to follow a finite mixture distribution with K components.
f(x) =\sum^K_{k=1} \underbrace{\omega_k}_{weight}\ \cdot \ \underbrace{g_k(X)}_{component} \qquad \tag{55.2}
- where g_k(x) is the density associated with G_k(x)
The values \omega_1, \ldots, \omega_K are usually called the “weights” of the mixture, and the distributions G_1 , \ldots, G_K are called the “components” of the mixture.
Each component will typically belong to a parametric family that is indexed by its own parameter \theta_k .
We will write G_k(x) = G_k (x \mid \theta_k ) whenever it is necessary to highlight the dependence on these parameters.
It is often the case that G_1, \ldots, G_K all belong to the same family and differ only in the value parameters associated with each of the distributions, so that G_k (x \mid \theta_k ) = G(x \mid \theta_k ). In that case, the function G (and sometimes its density/probability mass function g) are called the “kernel” of the mixture.
Example 55.1 (Three component Exponential mixture)
- For example, we could define a mixture with
- K = 3 components,
- with G(x \mid \theta_1 ), G(x \mid \theta_2 ) and G(x \mid \theta_3 ) all corresponding to exponential distributions with means \theta_1 , \theta_2 and \theta_3 respectively.
In that case, the cumulative distribution function of the mixture is given by
F(x) = \left(\omega_1 \left[ 1 − e^ {x \over \theta_1}\right] + \omega_2\left[ 1 − e^ {x \over \theta_2}\right] + \omega_3 \left[ 1 − e^ {x \over \theta_3}\right] \right)\mathbb{I}_{x\ge0} \qquad \tag{55.3}
f(x) = \left({\omega_1\over \theta_1} \left[ 1 − e^ {x \over \theta_1}\right] + {\omega_2\over \theta_2}\left[ 1 − e^ {x \over \theta_2}\right] + {\omega_3\over \theta_3} \left[ 1 − e^ {x \over \theta_3}\right] \right)\mathbb{I}_{x\ge0} \qquad \tag{55.4}
- Mixtures of normal can take more flexible form than an individual normal.
- We can use mixtures to create:
- Unimodal distributions Figure 55.12
- Bi-modal distribution c.f. Figure 55.8
- Multi-modal distributions.
- Heavy tailed distributions Figure 55.12
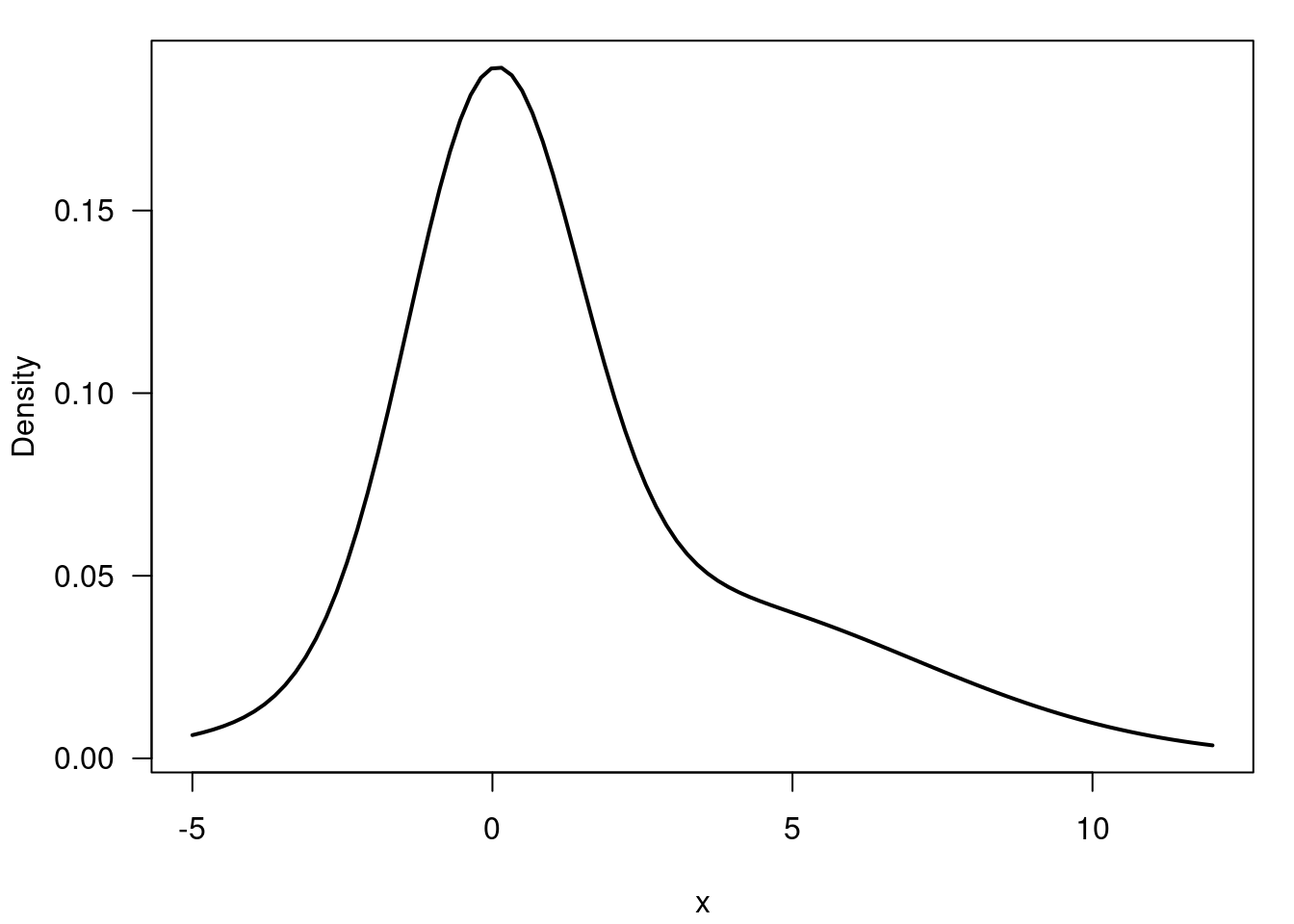
- Asymmetric distributions Figure 55.10
- Zero inflated distribution Figure 55.14 Figure 55.16
Example 55.2 (Location mixture of Normals)
- This is a mixture of Gaussian distributions with the same variance but different means.
- As the center of the normal distribution is based on the mean \mu_k, get get a mixture with similar normals at different locations.
f(x) = \sum_k \omega_k {1\over \sqrt{2 \pi \sigma}}e^{-{1\over 2 \sigma}(x-\mu_k)^2} \qquad \tag{55.5}
Example 55.3 (Location scale mixture of Normals)
- This time we have a mixture of Gaussian distributions with different means and variances.
- This allows us to create a mixture with different locations and scales.
f(x) = \sum_k \omega_k {1\over \sqrt{2 \pi \sigma_k}}e^{-{1\over 2 \sigma_k}(x-\mu_k)^2} \qquad \tag{55.6}
The expectation of a mixture is straightforward to compute, as it is a weighted sum of the expectations of the components.
the moment generating function of a mixture is also straightforward to compute, as it is a weighted sum of the moment generating functions of the components.
The variance of a mixture is not as straightforward to compute, as it involves the second moment of the components and the square of the expectation. However there is a degenerate case where the variance of the mixture is equal to the weighted sum of the variances of the components.
55.3 Mixtures of Gaussians 🎥
Here we will look at a few examples of mixtures of Gaussians which display different properties not available in a single Gaussian distribution. The video mostly walks through the code examples given in the readings below, while pointing out the features each of these mixtures possess that are not available in a single Gaussian distribution.
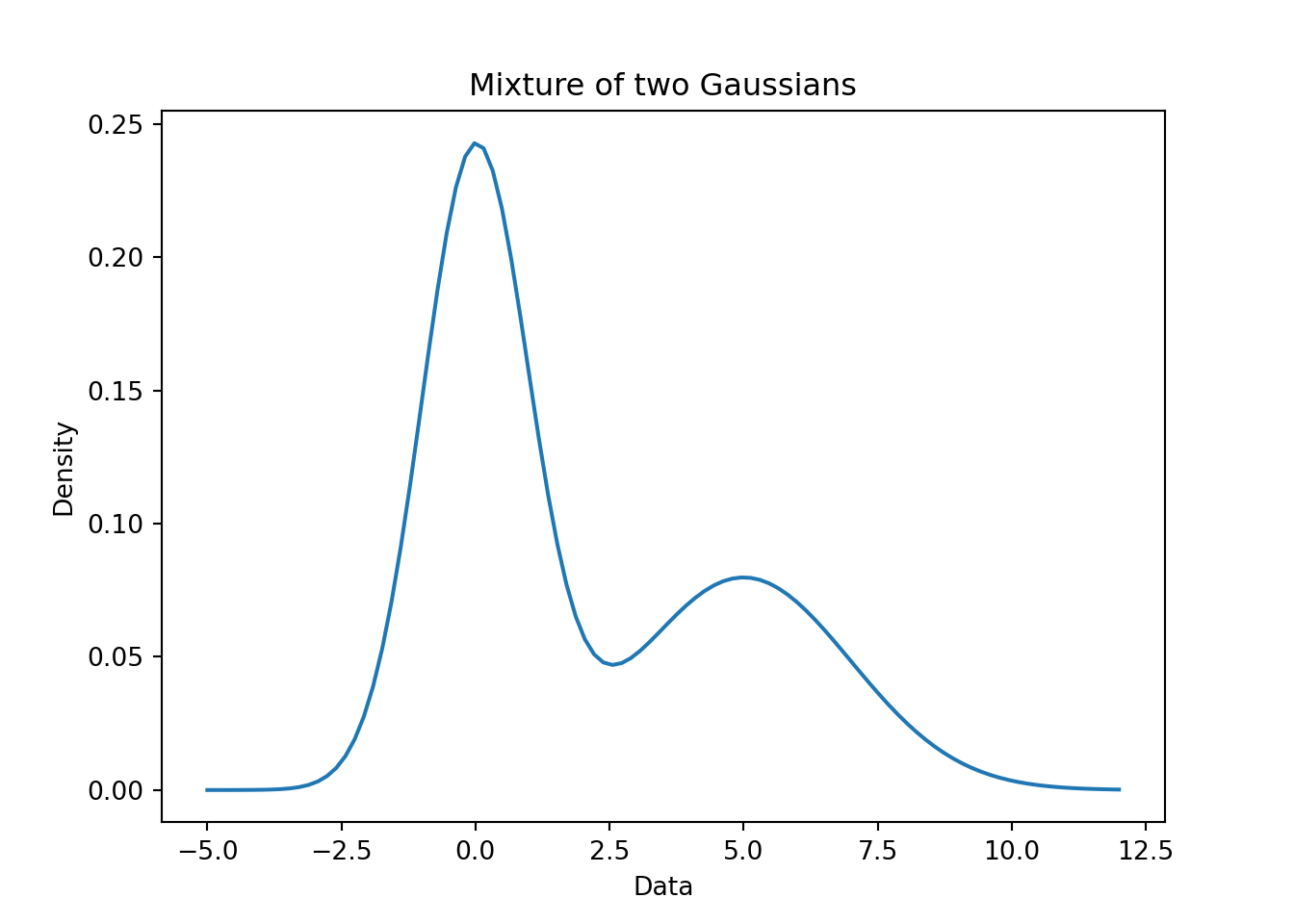
55.4 Example of a Bimodal mixture of Gaussians 🗒️ \mathcal{R} 🐍
# title: Mixture of univariate Gaussians, bimodal
from scipy.stats import norm
# Values to sample
x = np.linspace(-5, 12.0, num = 100)
# Normal 1 distribution
mu_1 = 0
std_1 = 1
r_n1 = norm.pdf(x,loc = mu_1, scale = std_1)
# Normal 2 Distribution
mu_2 = 5
std_2 = 2
r_n2 = norm.pdf(x, loc = mu_2, scale = std_2)
### computing mixture model
mixture_model = (0.6 * r_n1) + (0.4 * r_n2)
# Plotting the mixture models
fig, ax = plt.subplots(1, 1)
sns.lineplot(x=x, y=mixture_model)
plt.xlabel('Data')
plt.ylabel('Density')
plt.title('Mixture of two Gaussians')
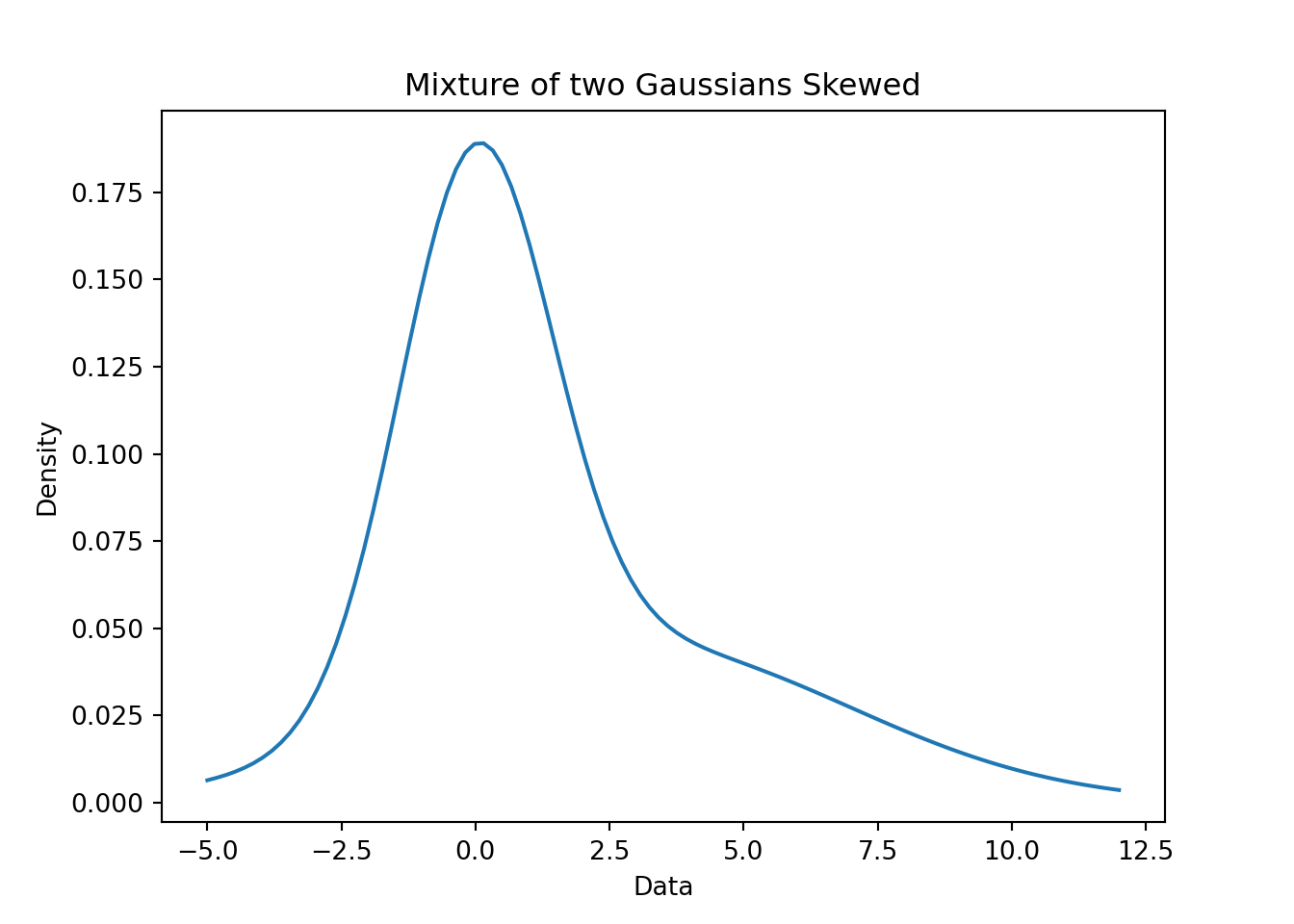
plt.show()plt.close()55.5 Example of a Uni-modal and skewed mixture of Gaussians 🗒️ \mathcal{R} 🐍
f(x) = 0.55 \times \mathcal{N}(0, 2) + 0.45 \times \mathcal{N}(3, 4) \qquad \tag{55.7}
# Values to sample
x = np.linspace(-5, 12.0, num = 100)
# Normal 1 distribution
mu_1 = 0
var_1 = 2
r_n1 = norm.pdf(loc = mu_1, scale = np.sqrt(var_1), x = x)
# Normal 2 Distribution
mu_2 = 3
var_2 = 16
r_n2 = norm.pdf(loc = mu_2, scale = np.sqrt(var_2), x = x)
### computing mixture model
mixture_model = (0.55 * r_n1) + (0.45 * r_n2)
# Plotting the mixture models
fig, ax = plt.subplots(1, 1)
sns.lineplot(x=x, y=mixture_model)
plt.xlabel('Data')
plt.ylabel('Density')
plt.title('Mixture of two Gaussians Skewed')
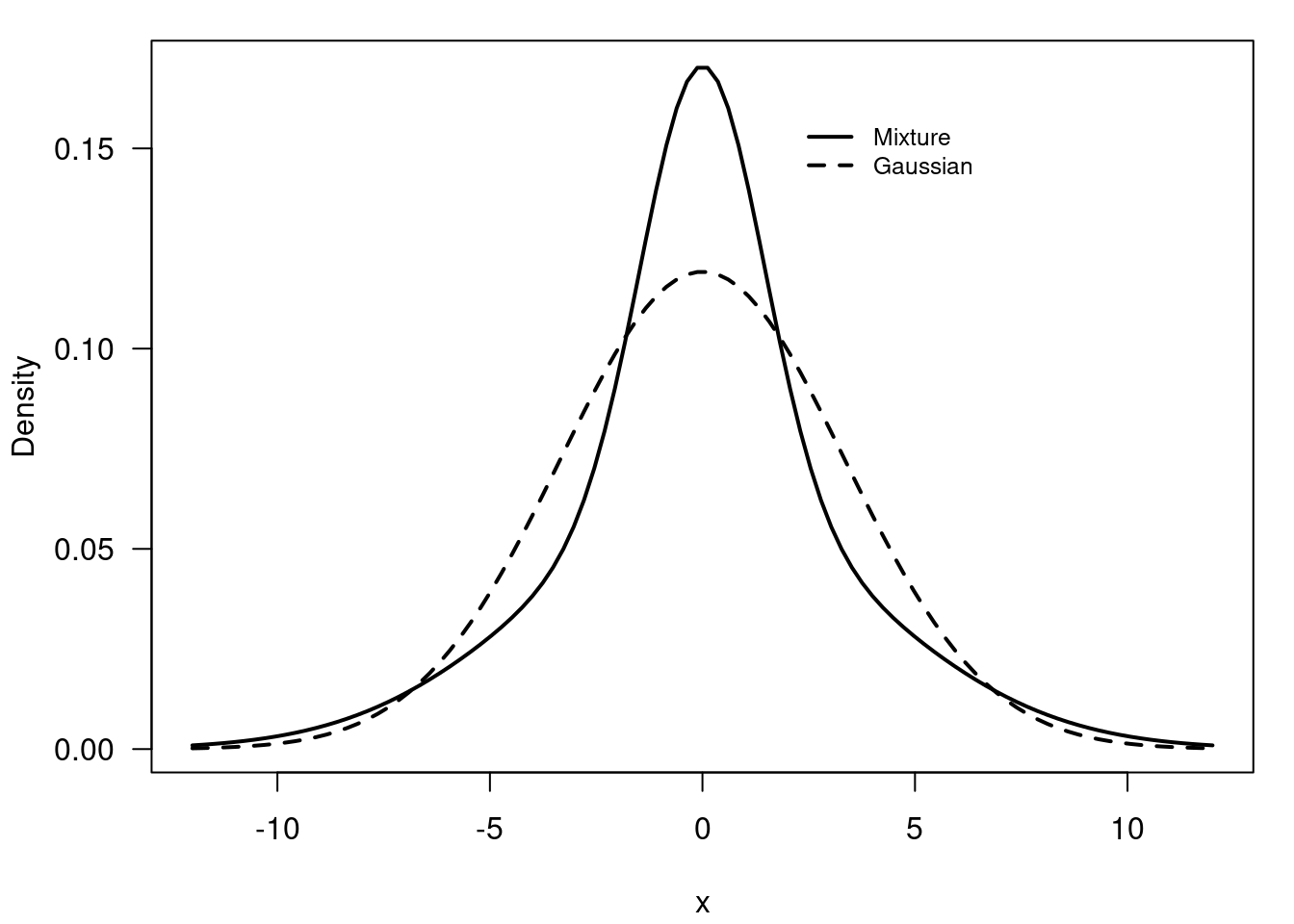
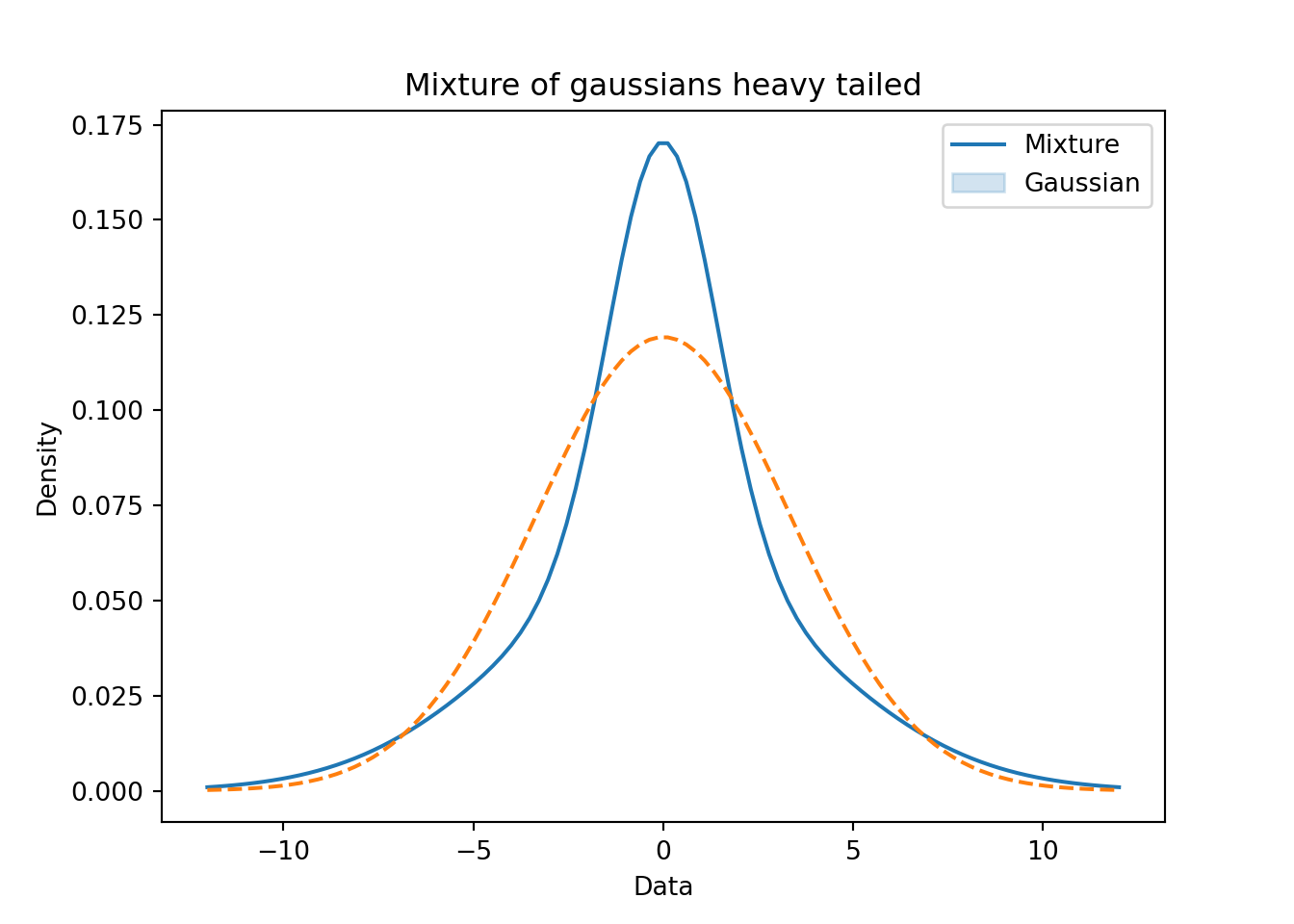
plt.show()plt.close()55.6 Example of a Uni-modal, symmetric and heavy tailed mixture of Gaussians 🗒️ \mathcal{R} 🐍
f(x) = 0.40 \times \mathcal{N}(0, 2) + 0.40 \times \mathcal{N}(0, 4) + 0.20 \times \mathcal{N}(0, 5) \qquad \tag{55.8}
# simulate Mixture of univariate Gaussians, unimodal heavy tail
x = seq(-12, 12, length=100)
y = 0.40 * dnorm(x, 0, sqrt(2)) +
0.40 * dnorm(x, 0, sqrt(16)) +
0.20 * dnorm(x, 0, sqrt(20))
z = dnorm(x, 0, sqrt(0.4*2 + 0.4*16 + 0.2*20))# Values to sample
x = np.linspace(-12.0, 12.0, num = 100)
# Normal 1 distribution
mu_1 = 0
var_1 = 2
r_n1 = norm.pdf(loc = mu_1, scale = np.sqrt(var_1), x = x)
# Normal 2 Distribution
mu_2 = 0
var_2 = 16
r_n2 = norm.pdf(loc = mu_2, scale = np.sqrt(var_2), x = x)
# Normal 3 Distribution
mu_3 = 0
var_3 = 20
r_n3 = norm.pdf(loc = mu_3, scale = np.sqrt(var_3), x = x)
### computing mixture model
y = (0.4 * r_n1) + (0.4 * r_n2) + (0.2 * r_n3)
z = norm.pdf(loc = 0, scale = np.sqrt(0.4 * 2 + 0.4 * 16 + 0.2 * 20), x = x)# Plotting the mixture models
fig, ax = plt.subplots(1, 1)
sns.lineplot(x=x, y=y)
ax.plot(x, z, '--')
plt.xlabel('Data')
plt.ylabel('Density')
plt.title('Mixture of gaussians heavy tailed')
plt.legend(['Mixture', 'Gaussian'])
plt.show()plt.close()55.7 Zero Inflated Mixtures 🎥
- Zero inflated distributions are useful for modeling data with excess zeros (often in term of count data).
- We learned in course 1 & 2 that the negative binomial or equivalent beta are zero inflated in comparison to the Poisson distribution.
- Today we see how we use mixture models by adding a point mass at zero to the distribution.
- Example from biology is the number of eggs in a nest.
- Example from insurance is the number of claims in a year.
- Example from survival analysis is the time to event data with a lot of censoring.
Note there are two approaches to zero inflation:
- One step models like the negative binomial.
- Hurdle models - two step models where we
- first model the zero inflation and
- then the count data This corresponds to the hierarchical representation of the mixture model.
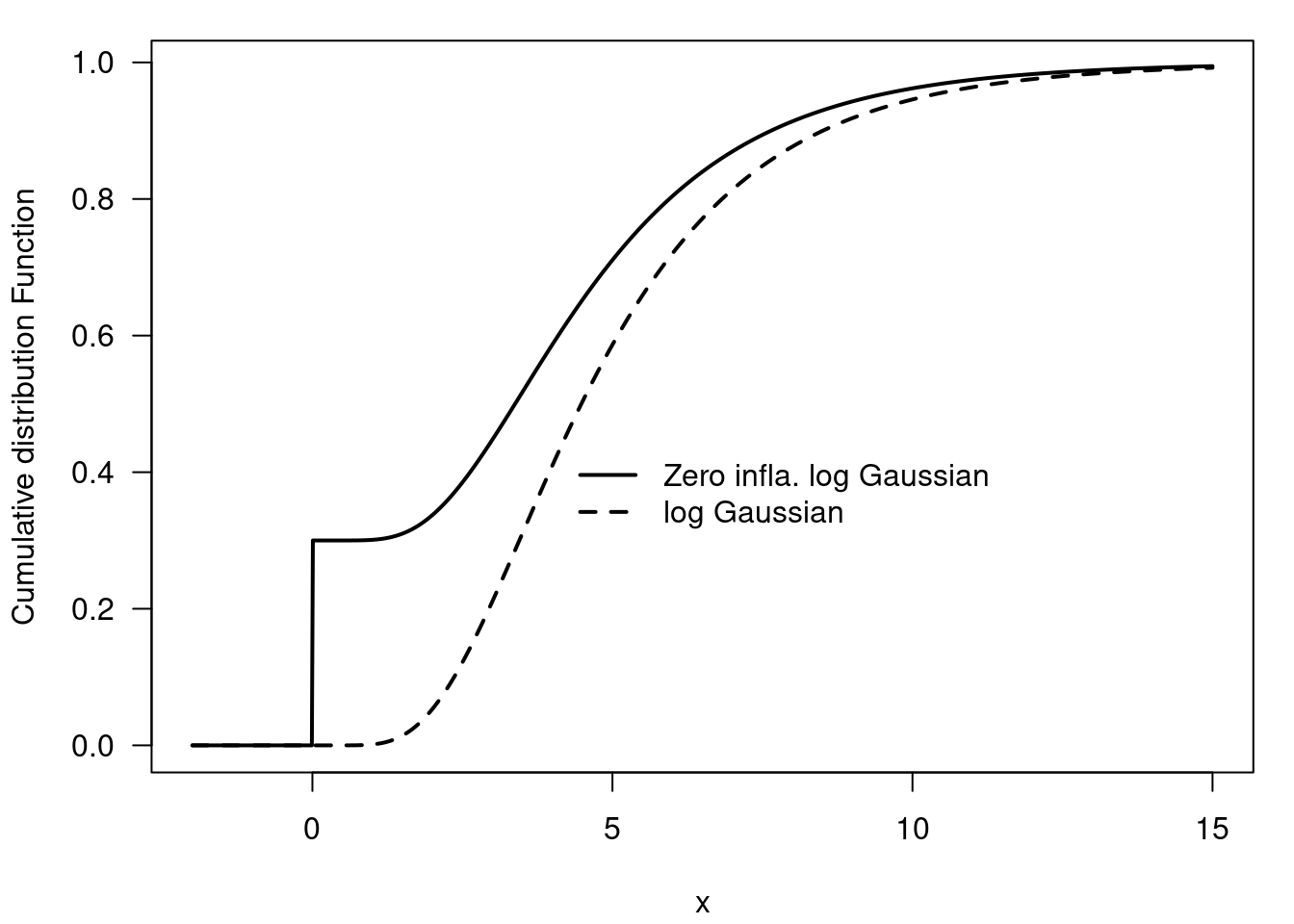
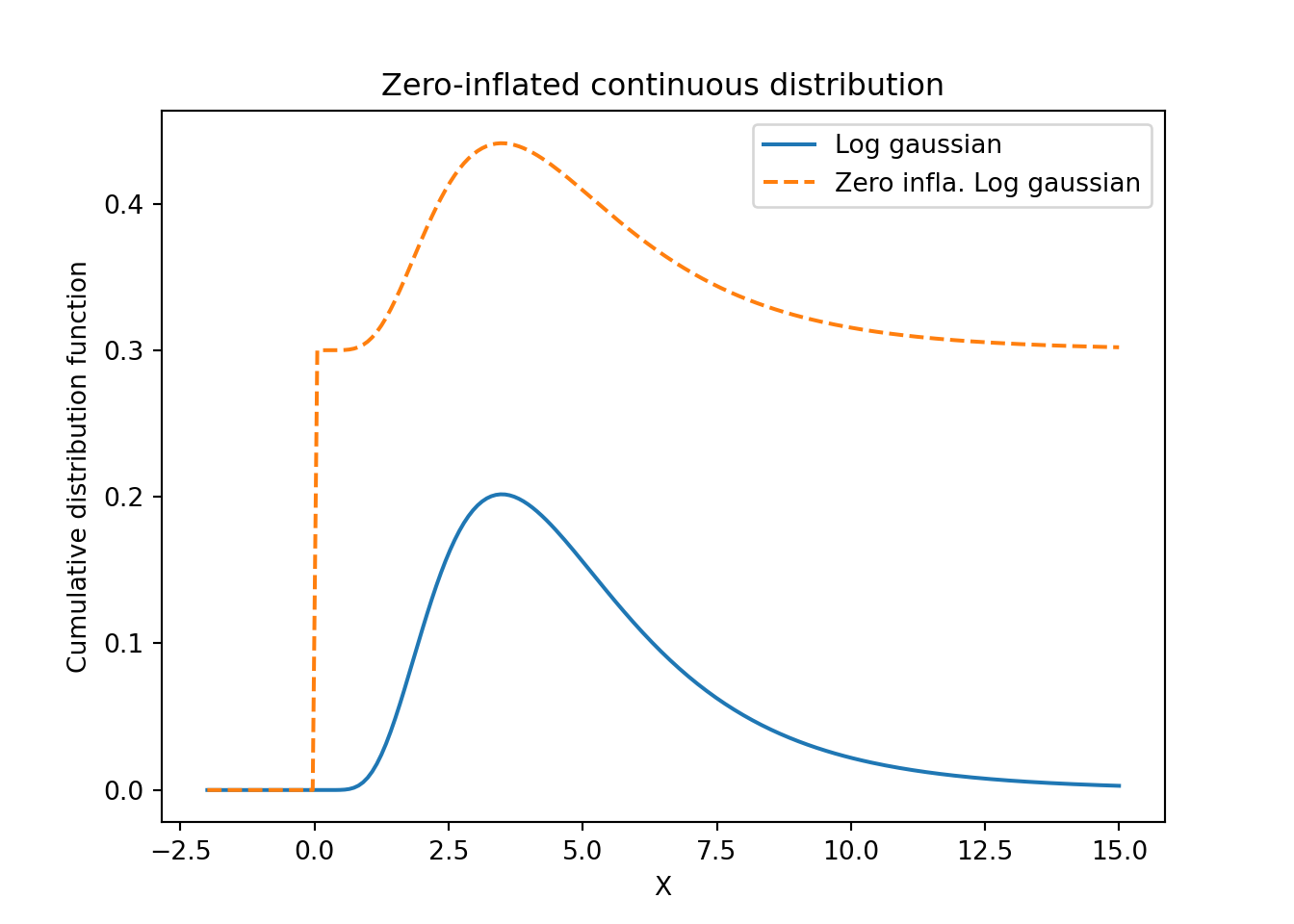
55.8 Example of a Zero-inflated log Gaussian distribution 🗒️ \mathcal{R} 🐍
This is a mixture of a point mass at zero and a log Gaussian distribution. This corresponds to the example where we have a light bulb factory and we want to model the time to failure of the light bulbs. We know that for the defective light bulbs, the time to failure is zero. For the non-defective light bulbs, the time to failure is log normally distributed with mean 1.5 and standard deviation 0.5
f(x) = 0.3 \times \mathbb{I}_{x\ge0} + 0.7 \times \mathcal{LN}(1.5, 0.5) \qquad \tag{55.9}
## The ZILN model
x = seq(-2, 15, length=1000)
y = plnorm(x, 1.5, 0.5)
z = 0.3*as.numeric(x>=0) + (1-0.3)*yimport numpy as np
import matplotlib.pyplot as plt
from scipy.stats import lognorm
# Zero-inflated continuous distribution
# Values to sample
x = np.linspace(-2.0, 15.0, num = 200)
# See for parameterization
y = lognorm.pdf(loc = 0, scale = np.exp(1.5), s = 0.5, x = x)
# Point mass vector
p_mass = np.zeros(len(x))
p_mass[x >= 0] = 1
z = 0.3 * p_mass + (1 - 0.3) * y## title: Zero inflated negative binomial distribution
# Plotting the mixture models
fig, ax = plt.subplots(1, 1)
ax.plot(x, y)
ax.plot(x, z, '--')
plt.xlabel('X')
plt.ylabel('Cumulative distribution function')
plt.title('Zero-inflated continuous distribution')
plt.legend(['Log gaussian', 'Zero infla. Log gaussian'])
plt.show()55.9 Example of a zero-inflated negative binomial distribution 🗒️ \mathcal{R} 🐍
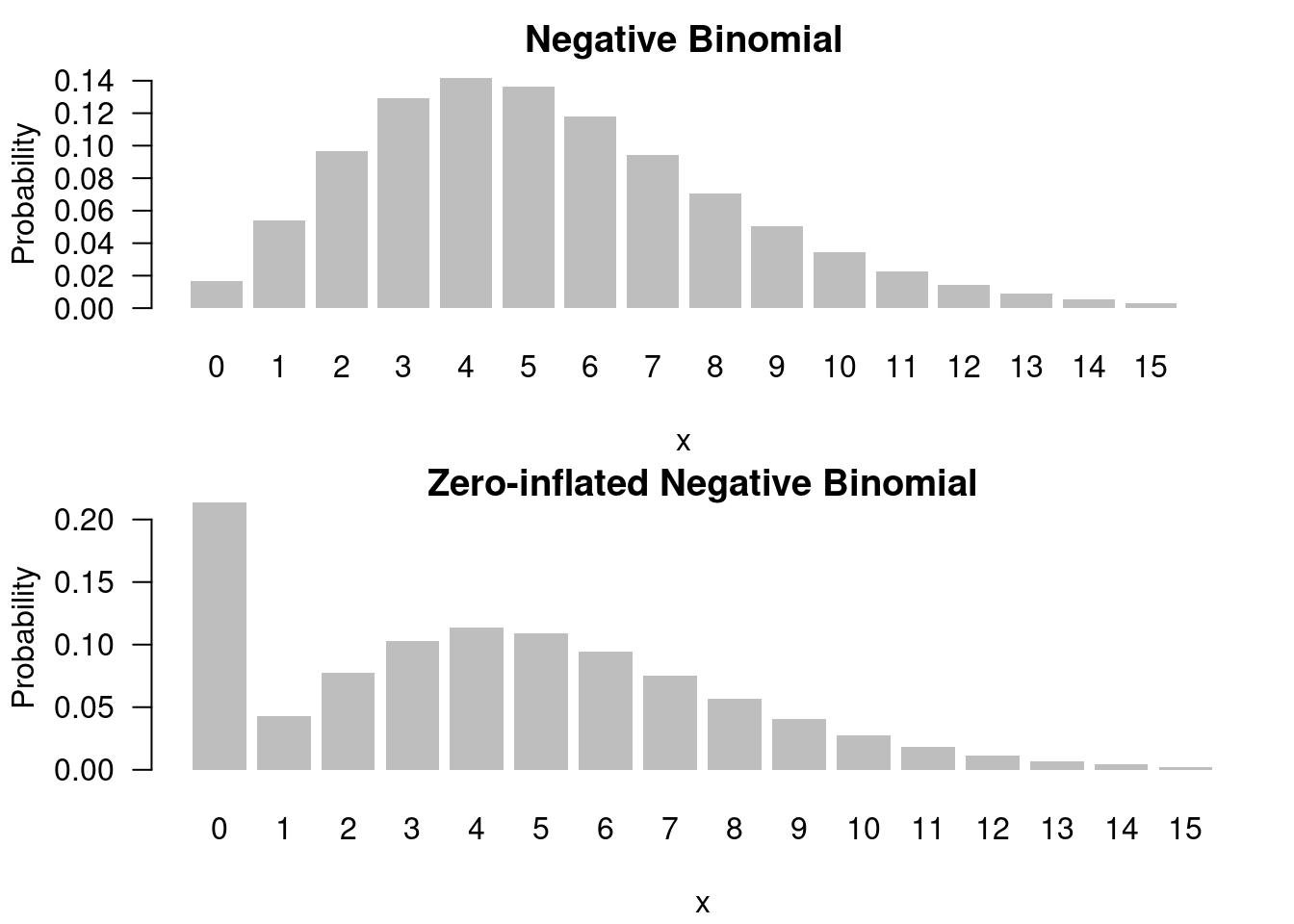
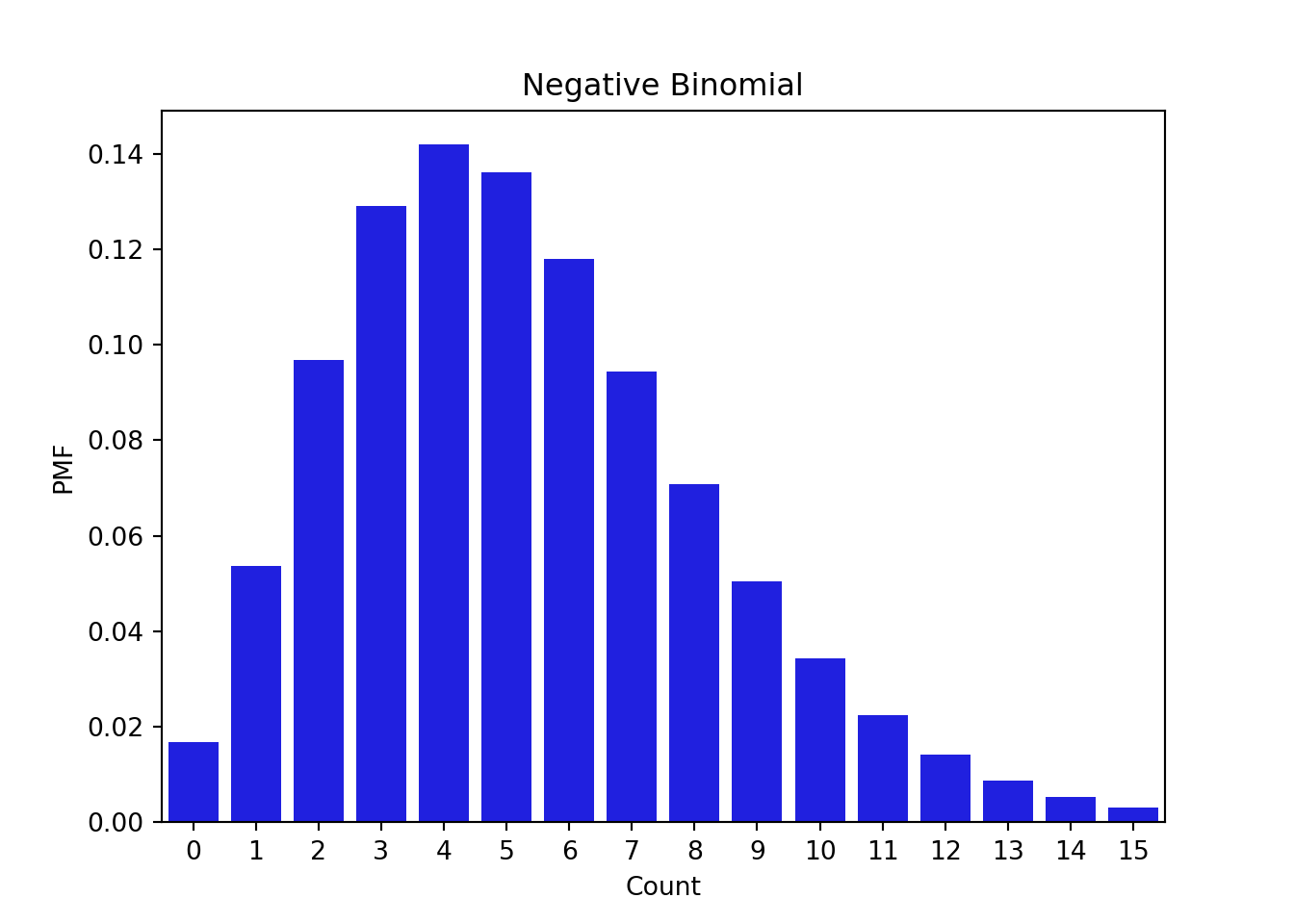
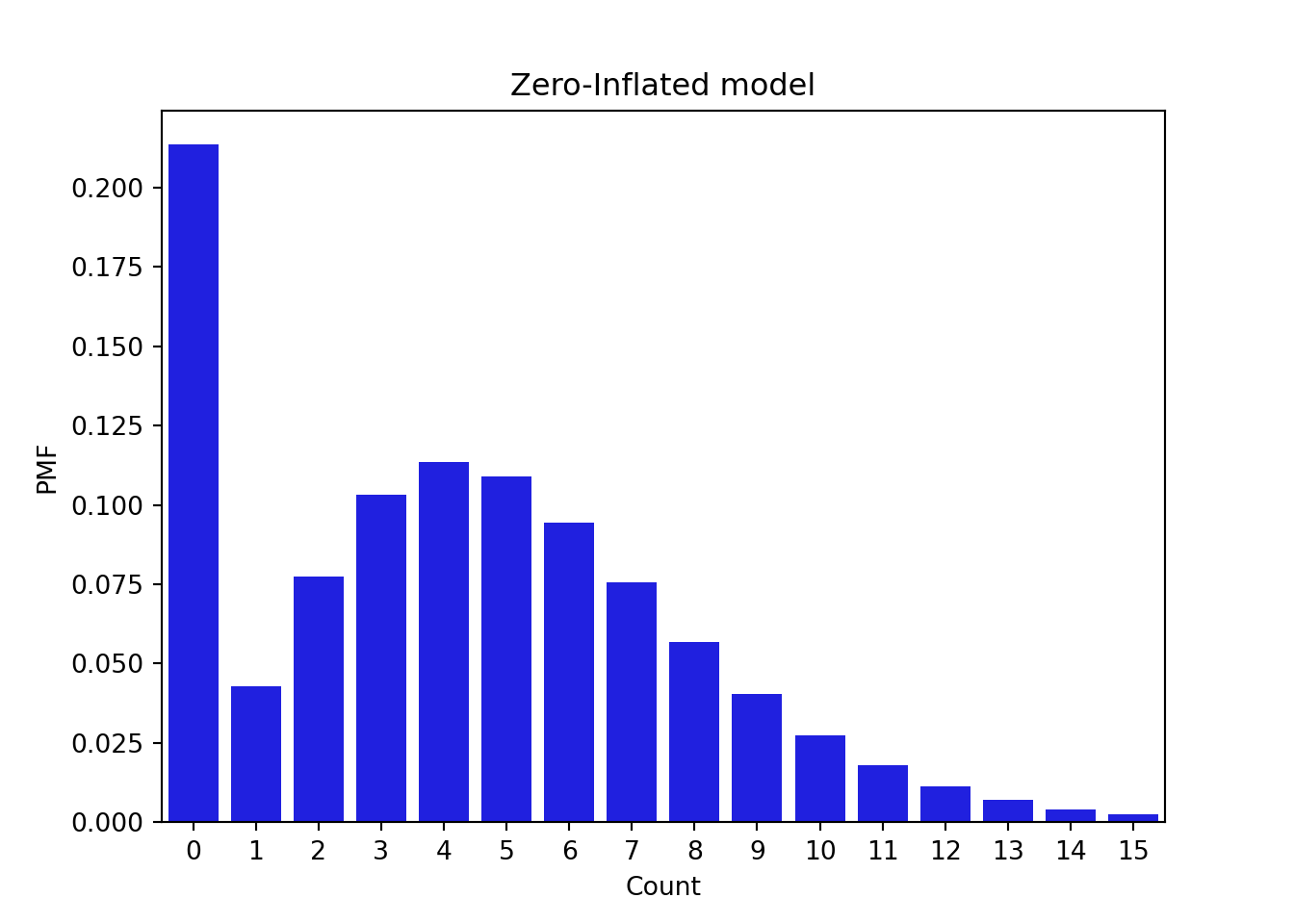
f(x) = 0.2 \times \mathbb{I}_{x=0} + 0.8 \times NB(8, 0.6) \qquad \tag{55.10}
## title: Zero inflated negative binomial distribution
x = seq(0, 15)
y = dnbinom(x, 8, 0.6)
z = 0.2*c(1,rep(0,length(x)-1)) + (1-0.2)*y
par(mfrow=c(2,1))
par(mar=c(4,4,2,2)+0.1)
barplot(y, names.arg=x, las=1, xlab = "x", ylab="Probability",
border=NA, main="Negative Binomial")
par(mar=c(4,4,1,1)+0.1)
barplot(z, names.arg=x, las=1, xlab = "x", ylab="Probability",
border=NA, main="Zero-inflated Negative Binomial")## title: Zero inflated negative binomial distribution
from scipy.stats import nbinom
import seaborn as sns
# Values to sample
x = np.arange(0, 16)
y = nbinom.pmf(x, n = 8, p = 0.6)
# Plotting the negative binomial model
fig, ax = plt.subplots(1, 1)
sns.barplot(x=x, y=y, color = 'blue')
plt.title('Negative Binomial')
plt.xlabel('Count')
plt.ylabel('PMF')
plt.show()# Point mass vector
p_mass = np.zeros(len(x))
p_mass[0] = 1
z = 0.2 * p_mass + (1 - 0.2) * y
# Plotting the zero-inflated model
fig, ax = plt.subplots(1, 1)
sns.barplot(x=x, y=z, color = 'blue')
plt.title('Zero-Inflated model')
plt.xlabel('Count')
plt.ylabel('PMF')
plt.show()