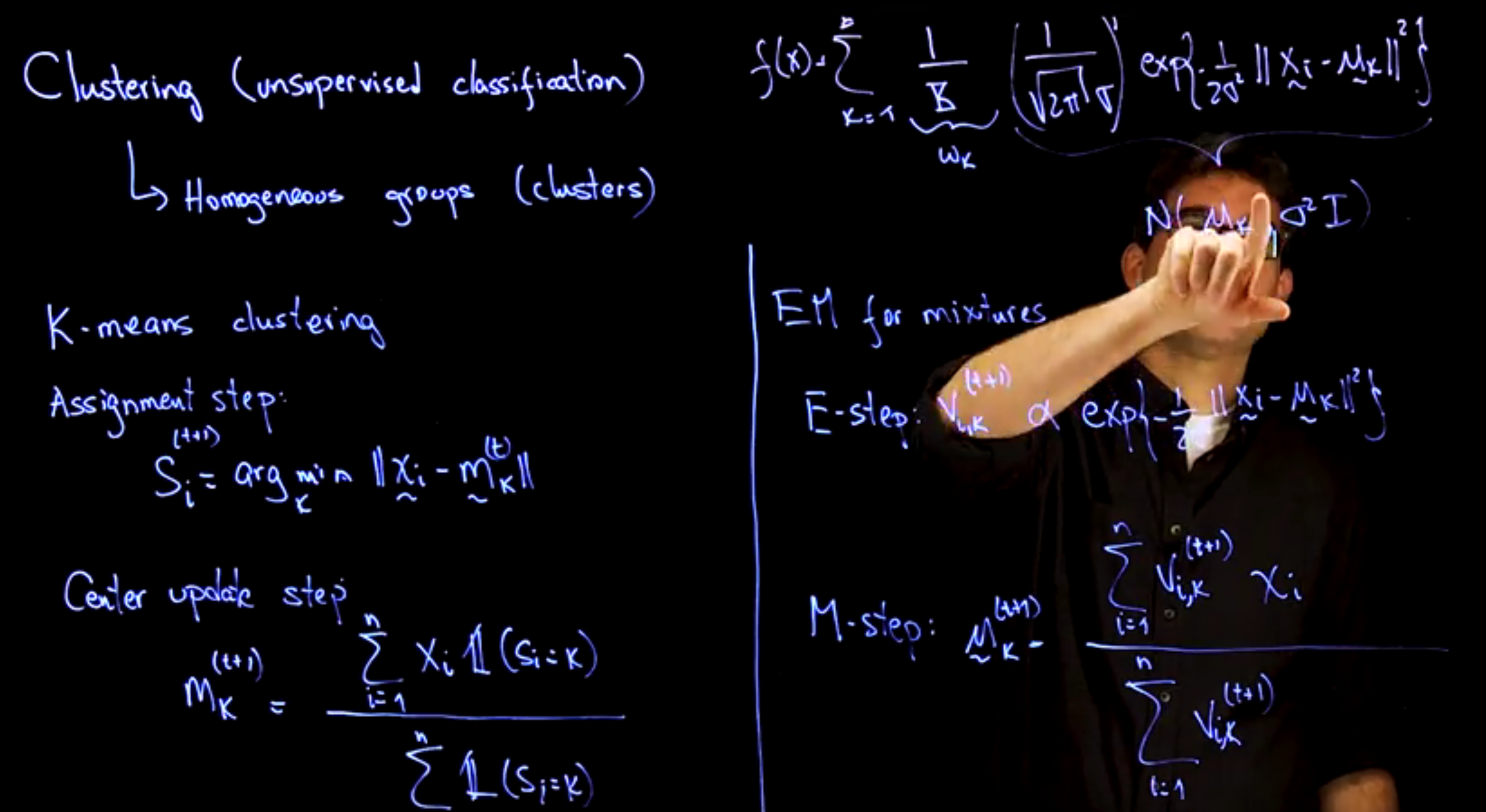---
title : 'Clustering - M4L6'
subtitle : 'Bayesian Statistics: Mixture Models - Applications'
categories:
- Bayesian Statistics
keywords:
- Mixture Models
- Clustering
- Notes
---
## Mixture Models for Clustering :movie_camera: {#sec-mixture-clustering}
{#fig-sl-01-clustering .column-margin width="53mm" group="slides"}
{#fig-sl-02-clustering .column-margin width="53mm" group="slides"}
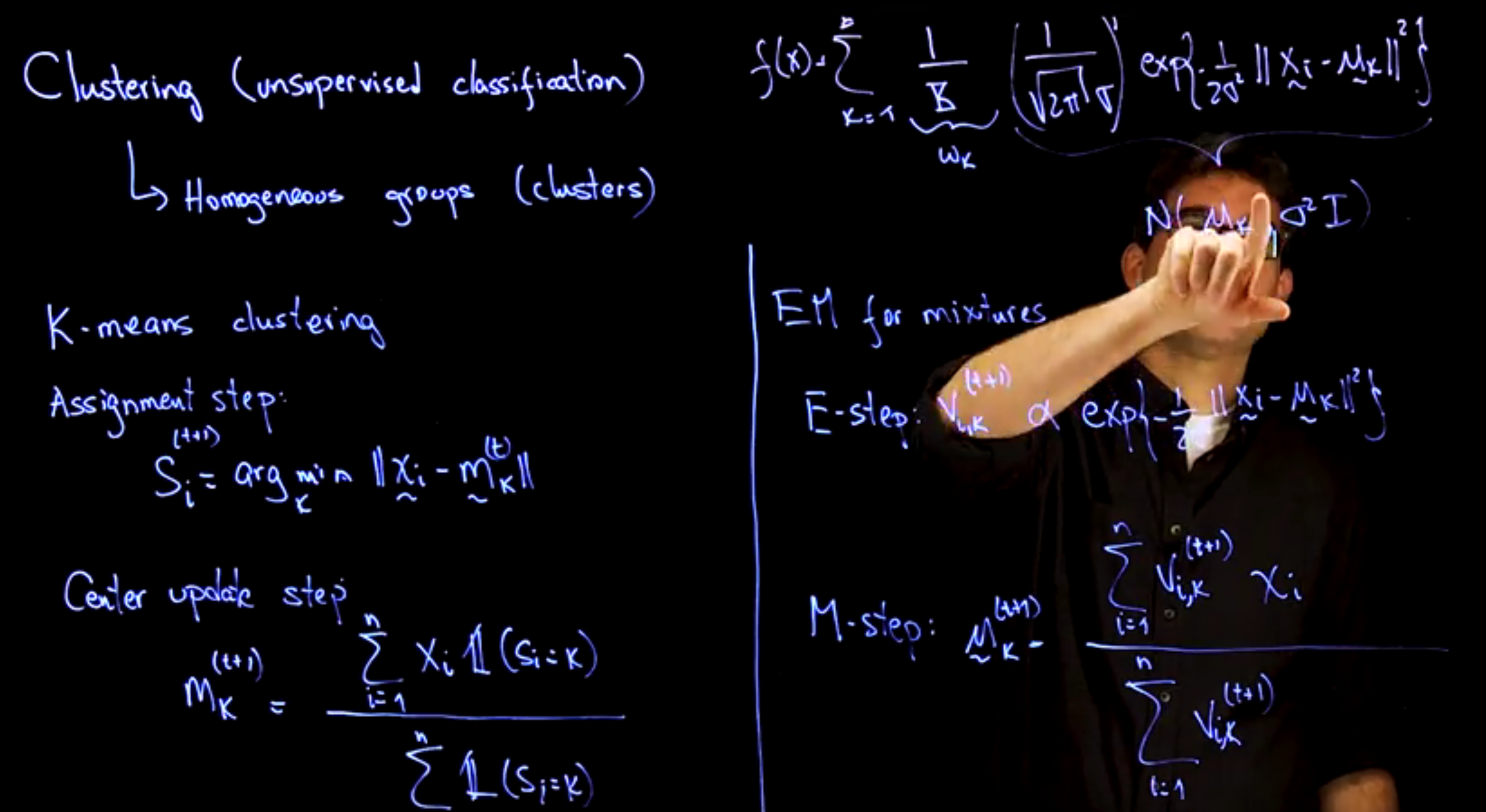{#fig-sl-03-clustering .column-margin width="53mm" group="slides"}
{#fig-sl-04-clustering .column-margin width="53mm" group="slides"}
\index{mixture!clustering}
\index{clustering}
Clustering, aims to partition heterogeneous data into homogeneous groups (clusters). Common in biology and other domains, clustering helps identify underlying structure, such as species based on physiological features.
A widely-used method is **K-means clustering**, which:
* Fixes the number of clusters $K$
* Alternates between:
1. **Assignment step**: Assigns each data point to its nearest cluster center.
2. **Update step**: Recomputes centers as means of assigned points.
This process iterates until assignments stabilize.
K-means is closely related to a **mixture of Gaussians** with:
* Equal component weights $\omega_k = 1/K$
* Shared spherical covariance $\Sigma_k = \sigma^2 I$
* Fitted via the **EM algorithm**, where:
* E-step: compute soft assignment probabilities $V_{ik}$
* M-step: update cluster means using weighted averages
If components are well-separated, EM approximates hard assignments similar to K-means.
### Limitations of K-means:
* Assumes **equal-sized spherical clusters**
* Fails with:
* **Correlated features**
* **Different variances per dimension**
* **Unequal cluster sizes**
### Advantages of Mixture Models:
* Allow flexible covariances $\Sigma_k$
* Estimate weights $\omega_k$
* Can use alternative kernels (e.g., t-distributions)
* Enable **Bayesian clustering** via MCMC
Thus, viewing K-means as a special case of Gaussian mixture models clarifies its assumptions and guides principled extensions.
## Clustering example :movie_camera: {#sec-mixture-clustering-example}
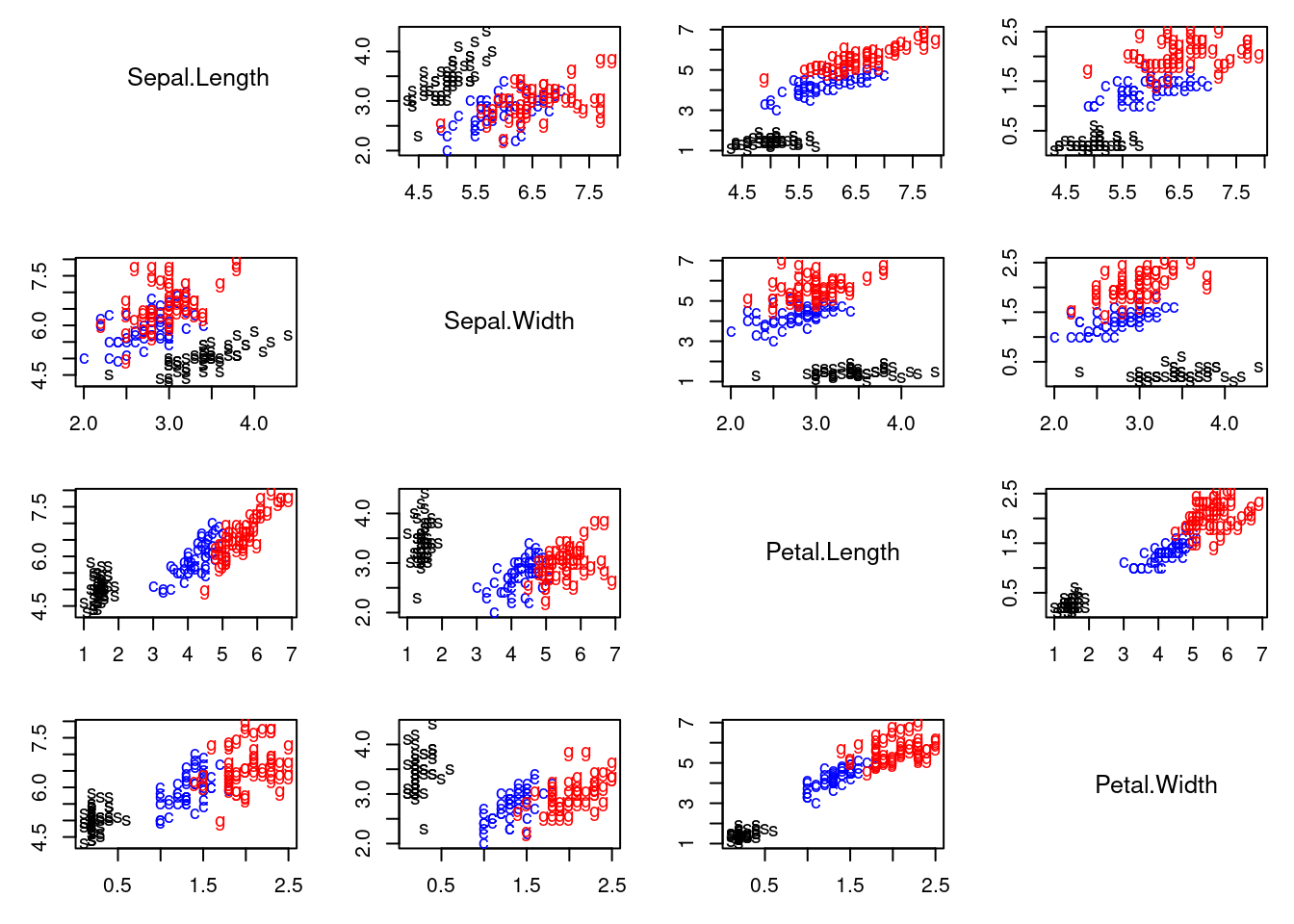
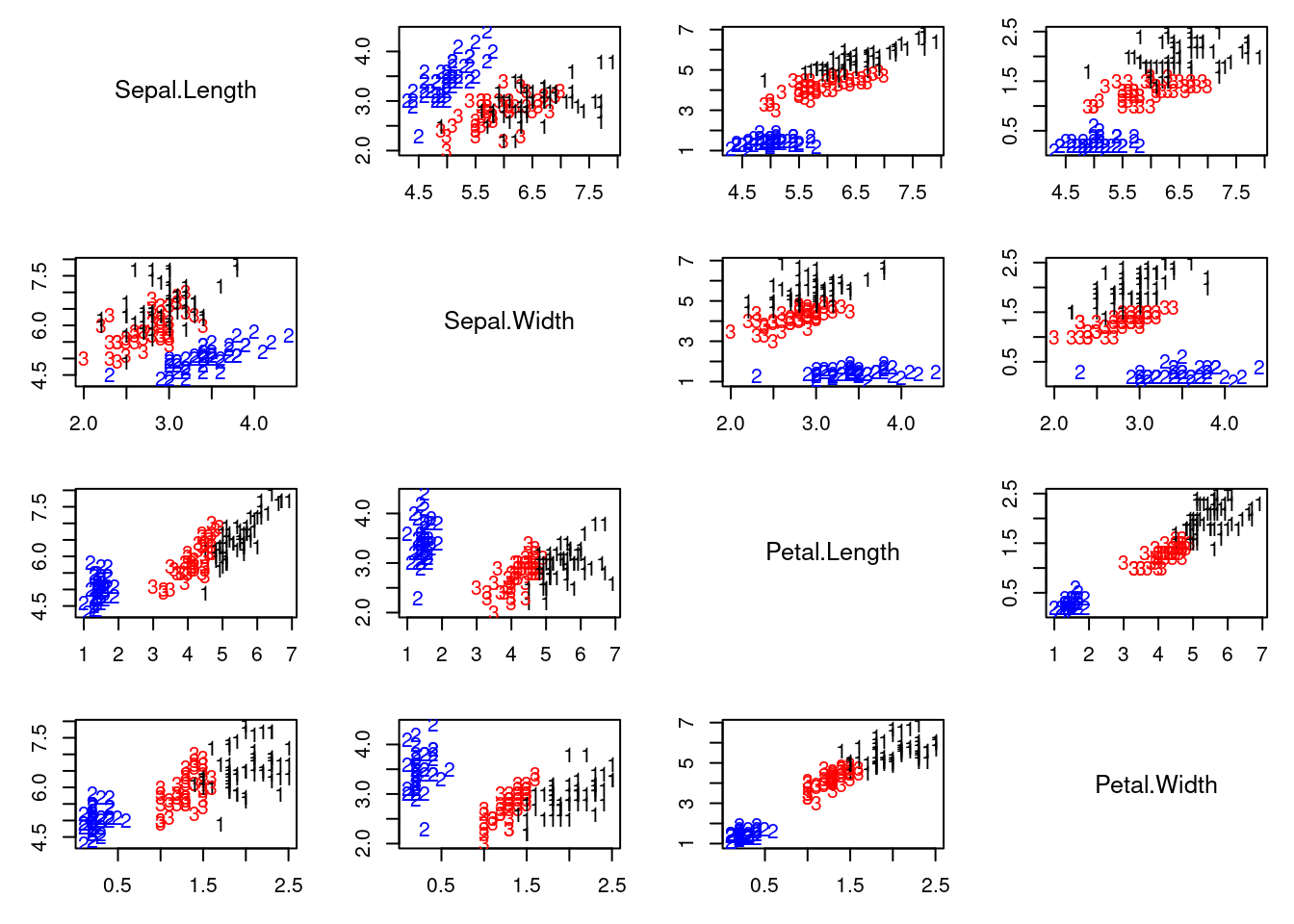
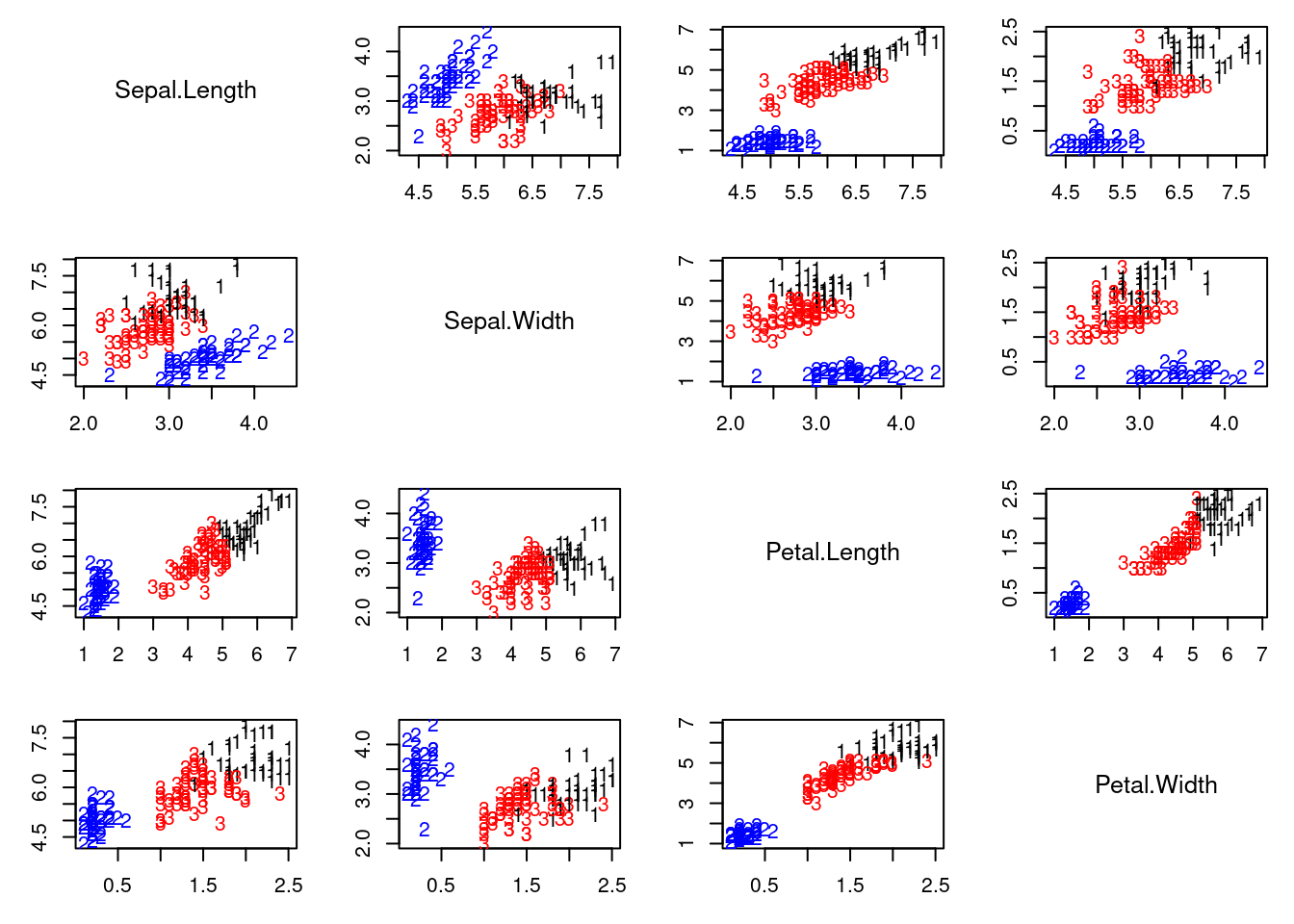
This video demonstrates clustering using the iris dataset, comparing K-means and a location and scale mixture model with $K$ normals. It highlights how mixture models can flexibly adapt to data structure, unlike K-means' rigid assumptions. The code is provided in
## Clustering example :spiral_notepad: $\mathcal{R}$ {#sec-clustering-code}
\index{dataset!iris}
```{r}
#| label: fig-clustering-iris
#| fig-cap: "Clustering the iris dataset using k-means clustering and a location and scale mixture model with K normals."
## Using mixture models for clustering in the iris dataset
## Compare k-means clustering and a location and scale mixture model with K normals
### Loading data and setting up global variables
rm(list=ls())
library(mclust)
library(mvtnorm)
### Defining a custom function to create pair plots
### This is an alternative to the R function pairs() that allows for
### more flexibility. In particular, it allows us to use text to label
### the points
pairs2 = function(x, col="black", pch=16, labels=NULL, names = colnames(x)){
n = dim(x)[1]
p = dim(x)[2]
par(mfrow=c(p,p))
for(k in 1:p){
for(l in 1:p){
if(k!=l){
par(mar=c(3,3,1,1)+0.1)
plot(x[,k], x[,l], type="n", xlab="", ylab="")
if(is.null(labels)){
points(x[,k], x[,l], pch=pch, col=col)
}else{
text(x[,k], x[,l], labels=labels, col=col)
}
}else{
plot(seq(0,5), seq(0,5), type="n", xlab="", ylab="", axes=FALSE)
text(2.5,2.5,names[k], cex=1.2)
}
}
}
}
## Setup data
data(iris)
x = as.matrix(iris[,-5])
n = dim(x)[1]
p = dim(x)[2] # Number of features
KK = 3
epsilon = 0.0000001
par(mfrow=c(1,1))
par(mar=c(4,4,1,1))
colscale = c("black","blue","red")
shortnam = c("s","c","g")
pairs2(x, col=colscale[iris[,5]], labels=shortnam[as.numeric(iris[,5])])
# Initialize the parameters of the algorithm
set.seed(63252)
numruns = 15
v.sum = array(0, dim=c(numruns, n, KK))
QQ.sum = rep(0, numruns)
for(ss in 1:numruns){
w = rep(1,KK)/KK #Assign equal weight to each component to start with
mu = rmvnorm(KK, apply(x,2,mean), 3*var(x)) #Cluster centers randomly spread over the support of the data
Sigma = array(0, dim=c(KK,p,p)) #Initial variances are assumed to be the same
Sigma[1,,] = var(x)
Sigma[2,,] = var(x)
Sigma[3,,] = var(x)
sw = FALSE
QQ = -Inf
QQ.out = NULL
s = 0
while(!sw){
## E step
v = array(0, dim=c(n,KK))
for(k in 1:KK){ #Compute the log of the weights
v[,k] = log(w[k]) + mvtnorm::dmvnorm(x, mu[k,], Sigma[k,,], log=TRUE)
}
for(i in 1:n){
v[i,] = exp(v[i,] - max(v[i,]))/sum(exp(v[i,] - max(v[i,]))) #Go from logs to actual weights in a numerically stable manner
}
## M step
w = apply(v,2,mean)
mu = matrix(0, nrow=KK, ncol=p)
for(k in 1:KK){
for(i in 1:n){
mu[k,] = mu[k,] + v[i,k]*x[i,]
}
mu[k,] = mu[k,]/sum(v[,k])
}
Sigma = array(0,dim=c(KK, p, p))
for(k in 1:KK){
for(i in 1:n){
Sigma[k,,] = Sigma[k,,] + v[i,k]*(x[i,] - mu[k,])%*%t(x[i,] - mu[k,])
}
Sigma[k,,] = Sigma[k,,]/sum(v[,k])
}
##Check convergence
QQn = 0
for(i in 1:n){
for(k in 1:KK){
QQn = QQn + v[i,k]*(log(w[k]) + mvtnorm::dmvnorm(x[i,],mu[k,],Sigma[k,,],log=TRUE))
}
}
if(abs(QQn-QQ)/abs(QQn)<epsilon){
sw=TRUE
}
QQ = QQn
QQ.out = c(QQ.out, QQ)
s = s + 1
}
v.sum[ss,,] = v
QQ.sum[ss] = QQ.out[s]
print(paste("ss =", ss))
}
## Cluster reconstruction under the mixture model
cc = apply(v.sum[which.max(QQ.sum),,], 1 ,which.max)
colscale = c("black","blue","red")
pairs2(x, col=colscale[cc], labels=cc)
ARImle = adjustedRandIndex(cc, as.numeric(iris[,5])) # Higher values indicate larger agreement
## Cluster reconstruction under the K-means algorithm
irisCluster <- kmeans(x, 3, nstart = numruns)
colscale = c("black","blue","red")
pairs2(x, col=colscale[irisCluster$cluster], labels=irisCluster$cluster)
ARIkmeans = adjustedRandIndex(irisCluster$cluster, as.numeric(iris[,5]))
```