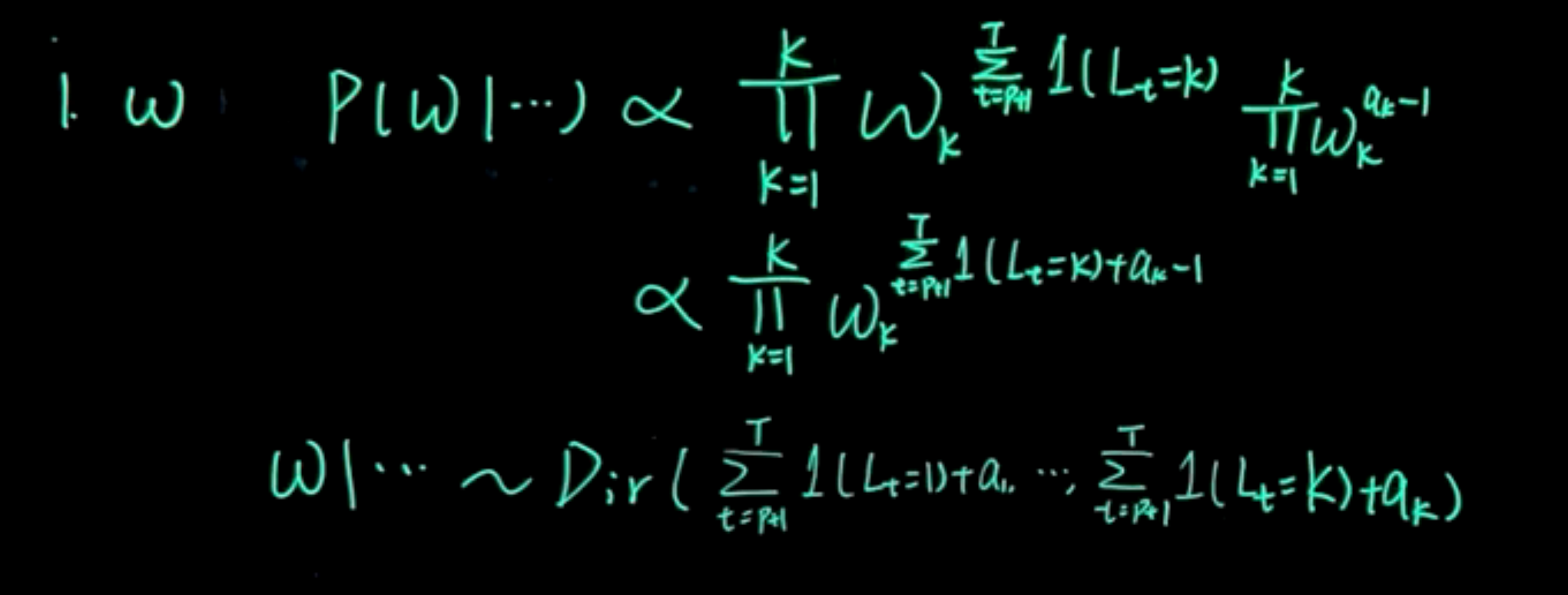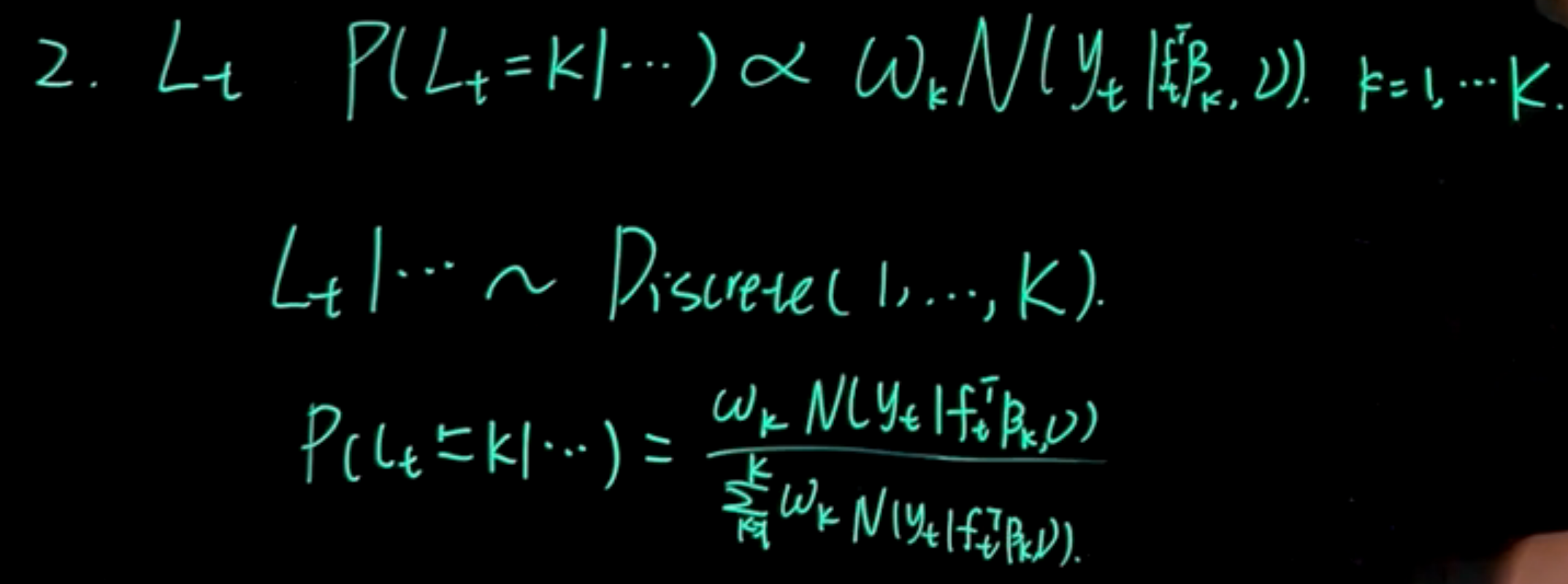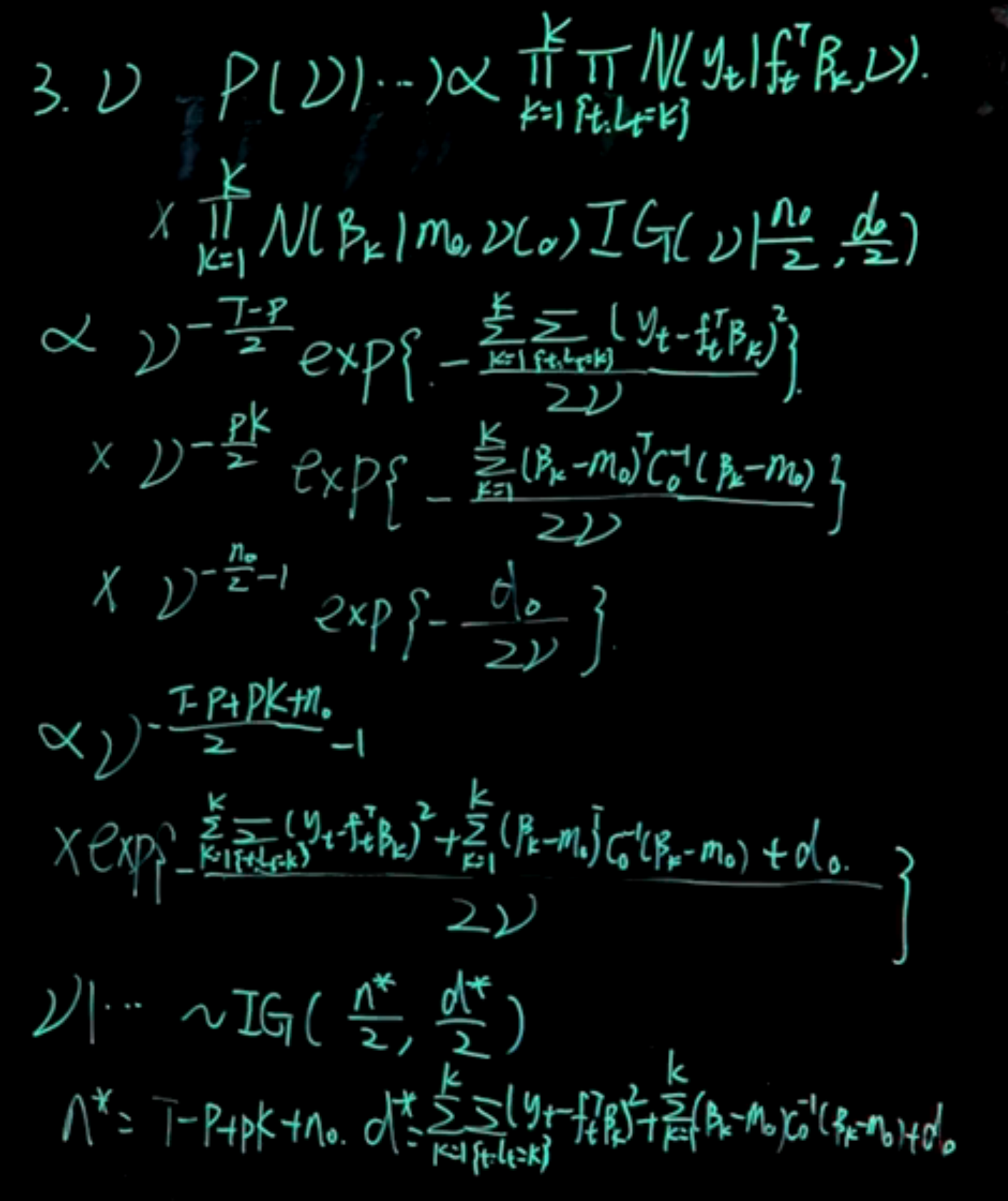## simulate data
y=c(-1,0,1)
n.all =200
for (i in 3:n.all) {
set.seed(i)
U=runif(1)
if(U<=0.5){
y.new=rnorm(1,0.1*y[i-1]+0.1*y[i-2],0.25)
}else if(U>0.8){
y.new=rnorm(1,0.3*y[i-1]+0.5*y[i-2],0.25)
}else{
y.new=rnorm(1,0.4*y[i-1]-0.5*y[i-2],0.25)
}
y=c(y,y.new)
}
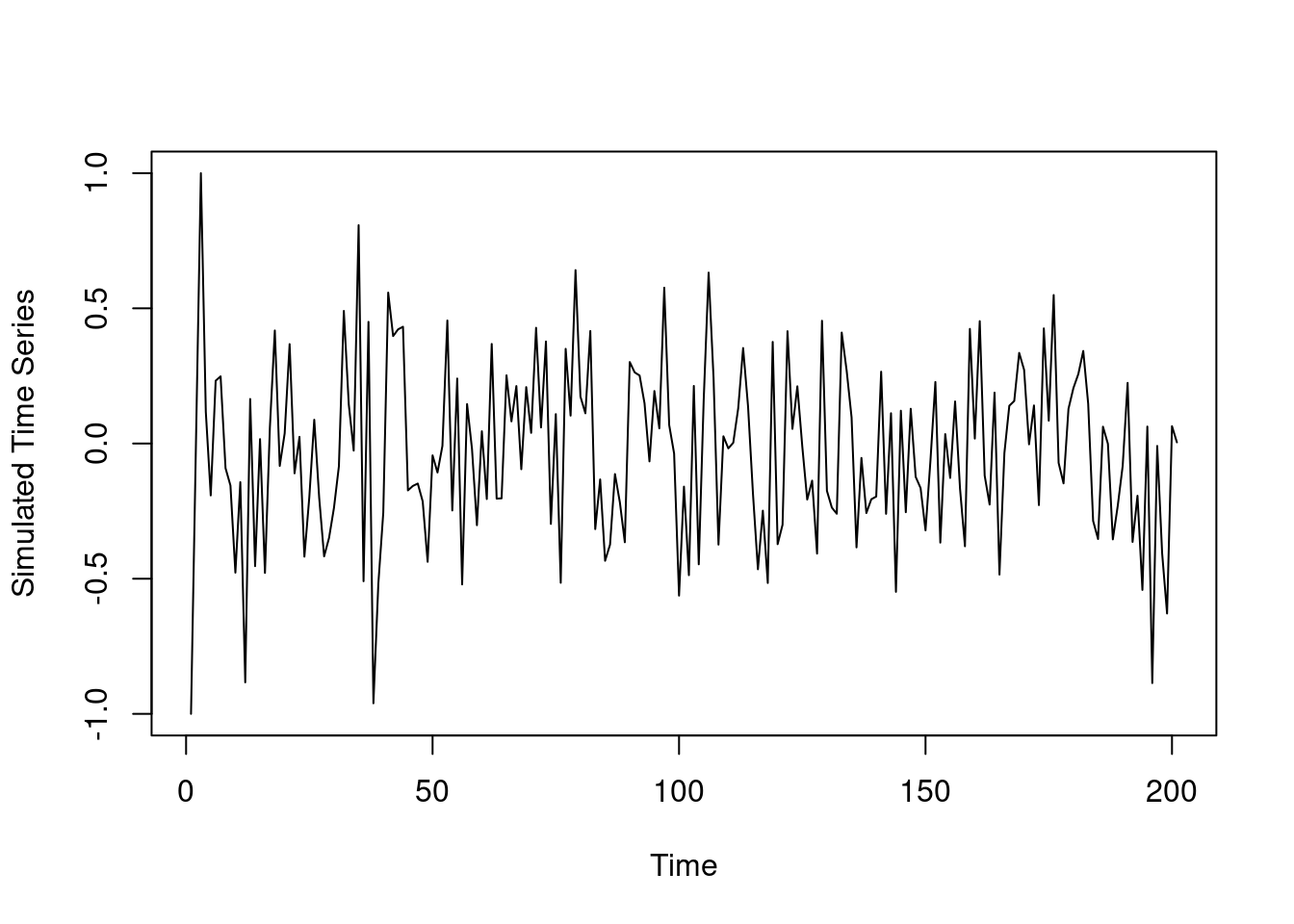
plot(y,type='l',xlab='Time',ylab='Simulated Time Series')110.1 The Location Mixture of AR Models 🎥
Unfortunately the course was missing the video with the derivation of the posterior from the hierarchical model of the location mixture of AR(p) models. However I have endeavored to fill this in using based on the final reading covering the more sophisticated location and scale mixture of AR(p).
The location mixture of AR(p) model for the data can be written hierarchically as follows:
\begin{aligned} &y_t\sim\sum_{k=1}^K\omega_kN(\mathbf{f}^T_t\boldsymbol{\beta}_k,\nu),\quad \mathbf{f}^T_t=(y_{t-1},\cdots,y_{t-p})^T,\quad t=p+1,\cdots,T\\ &\omega_k\sim Dir(a_1,\cdots,a_k),\quad \boldsymbol{\beta}_k\sim \mathcal{N}(\mathbf{m}_0,\nu_k\mathbf{C}_0),\quad \nu \sim \mathcal{IG}(\frac{n_0}{2},\frac{d_0}{2}) \end{aligned} \tag{110.1}
- where:
- \mathbf{f}_t is the design matrix of the AR model,
- \boldsymbol{\beta}_k is the coefficient vector for the k-th component,
- \nu_k is the variance for the k-th component, and
- \omega_k is the weight for the k-th component.
Introducing a latent configuration variable
\begin{aligned} L_t &: t \in \{1,2,\cdots,K\} \\ L_t &=k \iff y_t\sim N(\mathbf{f}^T_t\boldsymbol{\beta}_k,\nu) \end{aligned} \tag{110.2}
We denote: \boldsymbol{\beta}=(\beta_1,\cdots,\beta_K) \qquad \boldsymbol{\omega}=(\omega_1,\cdots,\omega_K)
\mathbf{L}=(L_1,\cdots,L_T)
we can write the full posterior distribution as:
p(\boldsymbol{\beta},\boldsymbol{\nu},\boldsymbol{\omega},\mathbf{L}\mid\mathbf{Y},\mathbf{F}) \propto p(\mathbf{Y}\mid\boldsymbol{\beta},\boldsymbol{\nu},\boldsymbol{\omega},\mathbf{F})p(\boldsymbol{\beta})p(\boldsymbol{\nu})p(\boldsymbol{\omega})p(\mathbf{L}) \tag{110.3}
where:
we can write the full posterior distribution as \begin{aligned} & \mathbb{P}r(\boldsymbol{\omega},\boldsymbol{\beta},\nu,\mathbf{L}|\mathbf{y},\mathbf{F}) \\ &\qquad \propto \mathbb{P}r(\mathbf{y}|\boldsymbol{\omega},\boldsymbol{\beta},\nu,\mathbf{L}) \\ &\qquad\qquad \mathbb{P}r(\mathbf{L}|\boldsymbol{\omega}) \\ &\qquad\qquad \mathbb{P}r(\boldsymbol{\omega}) \\ &\qquad\qquad \mathbb{P}r(\boldsymbol{\beta}) \\ &\qquad\qquad \mathbb{P}r(\nu)\\ &\qquad \propto \prod_{k=1}^K\prod_{\{t:L_t=k\}}N(y_t \mid \mathbf{f}^\top_t\boldsymbol{\beta}_k,\nu)\\ &\qquad \qquad \prod_{k=1}^K\omega_k^{\sum_{t=1}^T\mathbb{I}{(L_t=k)}} \quad \prod_{k=1}^K\omega_k^{a_k-1} \\ &\qquad\qquad\prod_{k=1}^K\left(\mathcal{N}(\boldsymbol{\beta}_k \mid \mathbf{m}_0,\mathbf{C}_0) \ \mathcal{IG}(\nu\mid\frac{n_0}{2},\frac{d_0}{2})\right) \end{aligned} \tag{110.4}
\begin{aligned} \mathbb{P}r(\omega,\beta,L,\nu \mid y) &\propto \prod_{k=1}^K \underbrace{ \prod_{t:L_t=k} \mathcal{N}(y_t \mid f_t^\top \beta_k,\nu) }_{ \text{Likelihood of the data } \mid \theta }\\ &\quad \qquad \underbrace{ \prod_{k=1}^K \omega_k^{\sum_{t=1}^T \mathbb{I}_{(L_t=k)}} \prod_{k=1}^K \omega_k^{a_k-1} }_{ \text{Prior for the weights }\omega }\\ &\quad \qquad \underbrace{ \prod_{k=1}^K \mathcal{N}(\beta_k \mid m_0, \nu C_0) }_{ \text{Prior for the AR coefficients} }\\ &\quad \qquad \underbrace{ \mathcal{IG}(\nu \mid \frac{n_0}{2},\frac{d_0}{2}) }_{ \text{Prior for the variance }\nu } \end{aligned} \tag{110.5}
110.2 Full conditional distributions of model parameters 🎥
\begin{aligned} \mathbb{P}r(\omega,\beta,L,\nu \mid y) &\propto \prod_{k=1}^K \underbrace{ \prod_{t:L_t=k} \mathcal{N}(y_t \mid f_t^\top \beta_k,\nu) }_{ \text{Likelihood of the data } \mid \theta }\\ &\quad \qquad \underbrace{ \prod_{k=1}^K \omega_k^{\sum_{t=1}^T \mathbb{1}_{(L_t=k)}} \prod_{k=1}^K \omega_k^{a_k-1} }_{ \text{Prior for the weights }\omega }\\ &\quad \qquad \underbrace{ \prod_{k=1}^K \mathcal{N}(\beta_k \mid m_0, \nu C_0) }_{ \text{Prior for the AR coefficients} }\\ &\quad \qquad \underbrace{ \mathcal{IG}(\nu \mid \frac{n_0}{2},\frac{d_0}{2}) }_{ \text{Prior for the variance }\nu } \end{aligned} \tag{110.6}
\begin{aligned} \mathbb{P}r(\omega,\beta,L,\nu \mid y) &\propto \prod_{k=1}^K \underbrace{ \prod_{t:L_t=k} \mathcal{N}(y_t \mid f_t^\top \beta_k,\nu) }_{ \text{Likelihood of the data } \mid \theta }\\ &\quad \qquad \underbrace{ \color{blue}\prod_{k=1}^K \omega_k^{\sum_{t=1}^T \mathbb{1}_{(L_t=k)}} \color{blue}\prod_{k=1}^K \omega_k^{a_k-1} }_{ \text{Prior for the weights }\omega }\\ &\quad \qquad \underbrace{ \prod_{k=1}^K \mathcal{N}(\beta_k \mid m_0, \nu C_0) }_{ \text{Prior for the AR coefficients} }\\ &\quad \qquad \underbrace{ \mathcal{IG}(\nu \mid \frac{n_0}{2},\frac{d_0}{2}) }_{ \text{Prior for the variance }\nu } \end{aligned}
\begin{aligned} \omega: \quad \mathbb{P}r(\omega\mid\cdots) &\sim \prod_{k=1}^K \omega_k^{\sum_{t=1}^T \mathbb{1}_{(L_t=k)}} \prod_{k=1}^K \omega_k^{a_k-1} \\ &\sim \prod_{k=1}^K \omega_k^{\sum_{t=1}^T \mathbb{1}_{(L_t=k)}+a_k-1} \\ &\sim Dir(a_1+\sum_{t=1}^T \mathbb{1}_{(L_t=1)}, \ldots, a_K+\sum_{t=1}^T \mathbb{1}_{(L_t=K)}) \end{aligned} \tag{110.7}
L_t: \quad \mathbb{P}r(L_t=k \mid \cdots) \sim \omega_k \mathcal{N}(y_t \mid f_t^\top \beta_k, \nu) \quad k=1,\ldots,K \tag{110.8}
L_t| \cdots \sim \textrm{Discrete}(1,\ldots,K) \tag{110.9}
Pr(L_t=k \mid \cdots) = \frac{\omega_k \mathcal{N}(y_t \mid f_t^\top \beta_k, \nu)}{\sum_{j=1}^K \omega_j \mathcal{N}(y_t \mid f_t^\top \beta_j, \nu)} \tag{110.10}
\begin{aligned} \mathbb{P}r(\nu \mid \cdots) &\propto \prod_{k=1}^K \prod_{t:L_t=k} \mathcal{N}(y_t \mid f_t^\top \beta_k,\nu) \\ & \qquad \prod_{k=1}^K \mathcal{N}(\beta_k \mid m_0, \nu C_0)\quad \mathcal{IG}(\nu \mid \frac{n_0}{2},\frac{d_0}{2}) \\ & \propto \nu^{-\frac{T-p}{2}} \exp\left( -\frac{\sum_{k=1}^K \sum_{t:L_t=k} (y_t - f_t^\top \beta_k)^2}{2\nu}\right) \\ & \quad \nu ^ {-\frac{pK}{2}} \exp\left( -\frac{1}{2\nu}\sum_{k=1}^K (\beta_k - m_0)^\top C_0^{-1} (\beta_k-m_0) (\beta_k - m_0)\right) \\ & \quad \nu ^{-\frac{n_0}{2} -1} \exp\left( -\frac{d_0}{2\nu}\right)\\ & \propto \nu^{-\frac{T-p+pK+n_0}{2}-1} \exp\left( -\frac{ \sum_{k=1}^K\sum_{t:L_t=k} (y_t - f_t^\top \beta_k)^2 +\sum_{k=1}^K (\beta_k - m_0)^\top C_0^{-1} (\beta_k - m_0) +d_0 }{2\nu}\right) \end{aligned}
\nu \mid \cdots \sim \mathcal{IG}\left(\frac{n^*}{2}, \frac{d^*}{2}\right)
n^* = T - p + n_0 \quad d^* = d_0 + \sum_{k=1}^K \sum_{t:L_t=k} (y_t - f_t^\top \beta_k)^2
\begin{aligned} \mathbb{P}r(\beta_k \mid \cdots) &\propto \prod_{t:L_t=k} \mathcal{N}(y_t \mid f_t^\top \beta_k,\nu) \mathcal{N}(\beta_k \mid m_0, \nu C_0) \\ \end{aligned}
We can think of this as a single component AR(p) model using only the part of data that satisfies this L_t=k criteria. \tilde{y}_k = y_{t:L_t=k} \qquad \tilde{F}_k \qquad n_k = \sum_{t:L_t=k} \mathbb{1}_{(L_t=k)}
\beta_k \mid \cdots \sim \mathcal{N}(m_k, C_k)
m = m_0 + C_0 \tilde{F}_k [\tilde{F}_k^\top C_0 \tilde{F}_k + I_n]^{-1} (\tilde{y}_k - \tilde{F}_k^\top m_0)
C = C_0 - C_0 \tilde{F}_k^\top [\tilde{F}_k C_0 \tilde{F}_k^\top + I_n]^{-1} \tilde{F}_k C_0
After we obtain posterior samples of model parameters, it is obvious to get ensemble posterior predictions.
\begin{aligned} \omega^{(s)} \quad \beta^{(s)} \quad \nu^{(s)} \\ y_t^{(s)} \quad p+1 \leq t \leq T \\ L_t^{(s)} \sim Discrete(\omega^{(s)})\\ y_t^{(s)} \sim N(f_t^\top \beta_{L_t^{(s)}},\nu_{L_t^{(s)}}) \end{aligned}
In this class, we will discuss the Gibbs sampler for obtaining posterior samples of model parameters as well as obtaining in-sample posterior predictions. Last time, we have derived for the mixture model, the full posterior distribution of model parameters have these huge form. We will start from here to find the full conditional distributions for each parameter. Let us start with the weight vector \omega. The full posterior distribution of \omega^{(s)} \mid \cdots, we will use this three dot to represent the correct conditioning.
Remember, to calculate full conditional distributions, we will select out from this full posterior distribution the specific terms that contains the variable of interest. Trying to recognize those terms as forming a kernel of a family that we know and can recognize.
This is a form of the kernel of the Dirichlet distribution.
110.3 Coding the Gibbs sampler
In this section we walk through some of the code in the next section.
110.4 Sample code for the Gibbs sampler
110.4.1 Step 1 Simulate data
We generate some data from the three component mixture of AR(2) process Given y_1=-1 and y_2=0 we generate y_3 to y_{3:200} from the following distribution:
\begin{aligned} y_i \sim 0.5\ \mathcal{N}(0.1 y_{t-1} + 0.1 y_{t-2}, 0.25) \\ +\ 0.3\ \mathcal{N}(0.4 y_{t-1} - 0.5 y_{t-2}, 0.25) \\ +\ 0.2\ \mathcal{N}(0.3 y_{t-1} + 0.5 y_{t-2}, 0.25) \end{aligned}
110.4.2 The prior
\begin{aligned} \omega &\sim Dir(a_1 \ldots a_k) \\ \beta_i &\sim \mathcal{N}(\mathbf{m}_0,\nu \mathbf{C}_0) \\ \nu &\sim \mathcal{IG}(n_0/2,d_0/2) \end{aligned} \tag{110.11}
## Model setup
library(MCMCpack) ## for dirichlet distributionLoading required package: codaLoading required package: MASS##
## Markov Chain Monte Carlo Package (MCMCpack)## Copyright (C) 2003-2025 Andrew D. Martin, Kevin M. Quinn, and Jong Hee Park##
## Support provided by the U.S. National Science Foundation## (Grants SES-0350646 and SES-0350613)
##library(mvtnorm) ## for multivariate normal distribution
p=2 ## order of AR process
K=3 ## number of mixing component
Y=matrix(y[3:200],ncol=1) ## y_{p+1:T}
Fmtx=matrix(c(y[2:199],y[1:198]),nrow=2,byrow=TRUE) ## design matrix F
n=length(Y) ## T-p
## prior hyperparameters
m0=matrix(rep(0,p),ncol=1) # weakly informative prior
C0=10*diag(p)
C0.inv=0.1*diag(p)
n0=0.02
d0=0.02
a=rep(1,K) ## parameter for dirichlet distribution#### MCMC setup
## number of iterations
nsim=20000
## store parameters
beta.mtx =matrix(0,nrow=p*K,ncol=nsim)
L.mtx =matrix(0,nrow=n,ncol=nsim)
omega.mtx=matrix(0,nrow=K,ncol=nsim)
nu.vec =rep(0,nsim)
## initial value
beta.cur=rep(0,p*K)
L.cur=rep(1,n)
omega.cur=rep(1/K,K)
nu.cur=1- 1
- we want 20,000 samples
- 2
- Each iteration requires p coefficients for K components, and there is one column per iteration.
- 3
-
L.mtxwill be a vector of length n, and there is one column per iteration. - 4
- The weights omega will be a vector of length K, and there is one column per iteration.
- 5
- We init \beta as 0 which means we assume all coefficients are 0 at the beginning.
- 6
-
We init
L.curas 1, assigning all observations initially to the first component. - 7
- We init the weights equally as 1/K, the number components,
- 8
- We init the variance \nu as 1
110.4.3 Helper functions to sample the full conditional distributions:
We use the following equations to sample from the full conditional
110.4.3.1 To sample for the weights \omega
The full conditional for \omega is given by:
\begin{aligned} \omega \mid \cdots &\sim Dir(a_1+\sum_{t=1}^T \mathbb{1}_{(L_t=1)}, \ldots, a_K+\sum_{t=1}^T \mathbb{1}_{(L_t=K)}) \end{aligned} \tag{110.12}
which we implement as follows:
#### sample functions
sample_omega=function(L.cur){
n.vec=sapply(1:K, function(k){sum(L.cur==k)})
rdirichlet(1,a+n.vec)
}- 1
-
this samples \omega using a Dirichlet RV parametrized by vector of sum of indicators from the current latent vars
L.cur
note that the sample_omega takes a parameter L.cur which is the current latent variable vector. This is used to count how many observations are assigned to each component.
110.4.3.2 To sample the latent variable L_t
Pr(L_t=k \mid \cdots) = \frac{\omega_k \mathcal{N}(y_t \mid f_t^\top \beta_k, \nu)}{\sum_{j=1}^K \omega_j \mathcal{N}(y_t \mid f_t^\top \beta_j, \nu)} \qquad k \in 1:K
sample_L_one=function(beta.cur,omega.cur,nu.cur,y.cur,Fmtx.cur){
prob_k=function(k){
beta.use=beta.cur[((k-1)*p+1):(k*p)]
omega.cur[k]*dnorm(y.cur,mean=sum(beta.use*Fmtx.cur),sd=sqrt(nu.cur))
}
prob.vec=sapply(1:K, prob_k)
L.sample=sample(1:K,1,prob=prob.vec/sum(prob.vec))
return(L.sample)
}
sample_L=function(y,x,beta.cur,omega.cur,nu.cur){
L.new=sapply(1:n, function(j){sample_L_one(beta.cur,omega.cur,nu.cur,y.cur=y[j,],Fmtx.cur=x[,j])})
return(L.new)
}- 2
- to sample the Configuration variable L probability of each one L_k for a single observation y_t
- 3
- this samples the latent variable for all observations
110.4.3.3 To sample \nu
\begin{aligned} \mathbb{P}r(\nu \mid \cdots) & \sim \mathcal{IG}(\nu \mid \frac{n^*}{2},\frac{d^*}{2}) \\ n^* &= T - p + n_0 \\ d^* &= \sum_{t:L_t=k} (y_t - f_t^\top \beta_k)^2 + \sum_{k=1}^K (\beta_k-m_0)^\top C_0^{-1} (\beta_k-m_0) + d_0 \end{aligned}
sample_nu=function(L.cur,beta.cur){
err.y=function(idx){
L.use = L.cur[idx]
beta.use = beta.cur[((L.use-1)*p+1):(L.use*p)]
err = Y[idx,]-sum(Fmtx[,idx]*beta.use)
return(err^2)
}
n.star=n0+n
d.star = d0+sum(sapply(1:n,err.y))
1/rgamma(1,shape=n.star/2,rate=d.star/2)
}- 4
- this samples the variance parameter
sample_beta=function(k,L.cur,nu.cur){
idx.select=(L.cur==k)
n.k=sum(idx.select)
if(n.k==0){
m.k=m0
C.k=C0
}else{
y.tilde.k=Y[idx.select,]
Fmtx.tilde.k=Fmtx[,idx.select]
e.k=y.tilde.k-t(Fmtx.tilde.k)%*%m0
Q.k=t(Fmtx.tilde.k)%*%C0%*%Fmtx.tilde.k+diag(n.k)
Q.k.inv=chol2inv(chol(Q.k))
A.k=C0%*%Fmtx.tilde.k%*%Q.k.inv
m.k=m0+A.k%*%e.k
C.k=C0-A.k%*%Q.k%*%t(A.k)
}
rmvnorm(1,m.k,nu.cur*C.k)
}- 5
- this samples the weights
110.4.3.4 To sample \beta:
- We denote :
- \tilde{y}_k := \{y_t : L_t=k\}
- \tilde{F}_k as the design matrix corresponding to \tilde{y}_k
- n_k = \sum_{t=1}^K \mathbb{I}_{(L_t=k)}
\beta_k \mid \cdots \sim \mathcal{N}(\mathbf{m}_k, \nu \mathbf{C}_k)
where:
\begin{aligned} \mathbf{m}_k &= \mathbf{m}_0+\mathbf{A}_k\mathbf{e}_k, &\mathbf{C}_k &= \mathbf{C}_0-\mathbf{A}_k\mathbf{Q}_k\mathbf{A}_k^{T} \\ \mathbf{e}_k &= \mathbf{\tilde{y}}_k-\mathbf{\tilde{F}}_k^T\mathbf{m}_0, &\mathbf{Q}_k &= \mathbf{\tilde{F}}_k^T\mathbf{C}_0\mathbf{\tilde{F}}_k+\mathbf{I}_{n_k}, \\ \mathbf{A}_k &= \mathbf{C}_0\mathbf{\tilde{F}}_k\mathbf{Q}_k^{-1} \\ n_k^* &= n_0+n_k, &d_k^* &= d_0+\mathbf{e}_k^T\mathbf{Q}_k^{-1}\mathbf{e}_k \end{aligned}
## Gibbs Sampler
for (i in 1:nsim) {
set.seed(i)
## sample omega
omega.cur=sample_omega(L.cur)
omega.mtx[,i]=omega.cur
## sample L
L.cur=sample_L(Y,Fmtx,beta.cur,omega.cur,nu.cur)
L.mtx[,i]=L.cur
## sample nu
nu.cur=sample_nu(L.cur,beta.cur)
nu.vec[i]=nu.cur
## sample beta
beta.cur=as.vector(sapply(1:K, function(k){sample_beta(k,L.cur,nu.cur)}))
beta.mtx[,i]=beta.cur
## show the numer of iterations
if(i%%1000==0){
print(paste("Number of iterations:",i))
}
}[1] "Number of iterations: 1000"
[1] "Number of iterations: 2000"
[1] "Number of iterations: 3000"
[1] "Number of iterations: 4000"
[1] "Number of iterations: 5000"
[1] "Number of iterations: 6000"
[1] "Number of iterations: 7000"
[1] "Number of iterations: 8000"
[1] "Number of iterations: 9000"
[1] "Number of iterations: 10000"
[1] "Number of iterations: 11000"
[1] "Number of iterations: 12000"
[1] "Number of iterations: 13000"
[1] "Number of iterations: 14000"
[1] "Number of iterations: 15000"
[1] "Number of iterations: 16000"
[1] "Number of iterations: 17000"
[1] "Number of iterations: 18000"
[1] "Number of iterations: 19000"
[1] "Number of iterations: 20000"#### show the result
sample.select.idx=seq(10001,20000,by=1)
post.pred.y.mix=function(idx){
k.vec.use=L.mtx[,idx]
beta.use=beta.mtx[,idx]
nu.use=nu.vec[idx]
get.mean=function(s){
k.use=k.vec.use[s]
sum(Fmtx[,s]*beta.use[((k.use-1)*p+1):(k.use*p)])
}
mu.y=sapply(1:n, get.mean)
sapply(1:length(mu.y), function(k){rnorm(1,mu.y[k],sqrt(nu.use))})
}
y.post.pred.sample=sapply(sample.select.idx, post.pred.y.mix)
summary.vec95=function(vec){
c(unname(quantile(vec,0.025)),mean(vec),unname(quantile(vec,0.975)))
}
summary.y=apply(y.post.pred.sample,MARGIN=1,summary.vec95)
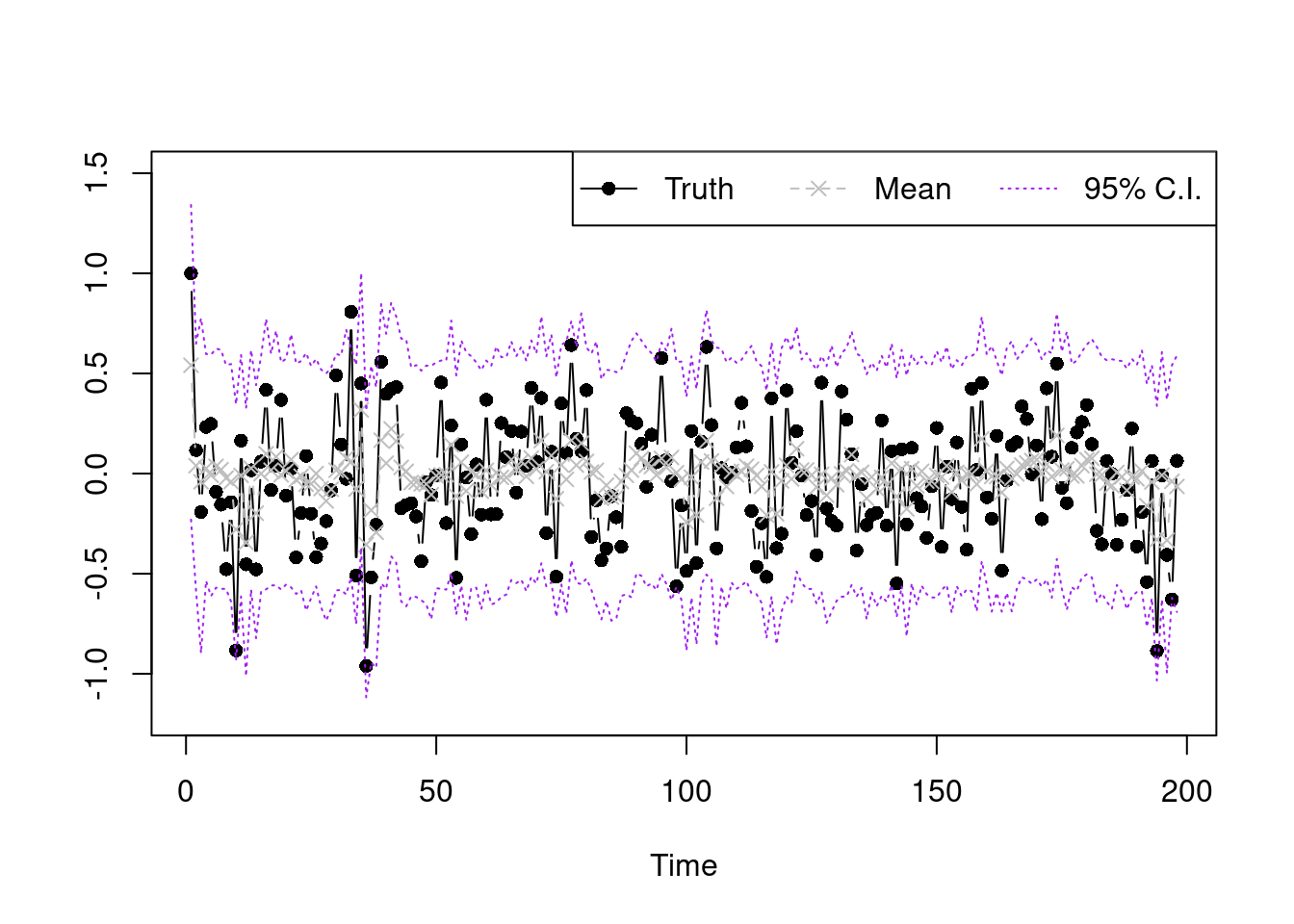
plot(Y,type='b',xlab='Time',ylab='',pch=16,ylim=c(-1.2,1.5))
lines(summary.y[2,],type='b',col='grey',lty=2,pch=4)
lines(summary.y[1,],type='l',col='purple',lty=3)
lines(summary.y[3,],type='l',col='purple',lty=3)
legend("topright",legend=c('Truth','Mean','95% C.I.'),lty=1:3,
col=c('black','grey','purple'),horiz = T,pch=c(16,4,NA))