logistic regression, Bayesian statistics, R programming, statistical modeling, classification, binary outcomes
Logistic regression is the preferred model when modelling a problem where the response variable is binary such as a classification or the outcome of a Bernoulli trial. In such the traditional least square fit suffers from a number of shortcomings. The main idea here is a log transform. However a naïve approach this transform imposes issues with 0 valued inputs since log(0)=-\infty
For an example of logistic regression , we’ll use the urine data set from the boot package in R. The response variable is r, which takes on values of 0 or 1. We will remove some rows from the data set which contain missing values.
library("boot")
data("urine")
?urine
head(urine) r gravity ph osmo cond urea calc
1 0 1.021 4.91 725 NA 443 2.45
2 0 1.017 5.74 577 20.0 296 4.49
3 0 1.008 7.20 321 14.9 101 2.36
4 0 1.011 5.51 408 12.6 224 2.15
5 0 1.005 6.52 187 7.5 91 1.16
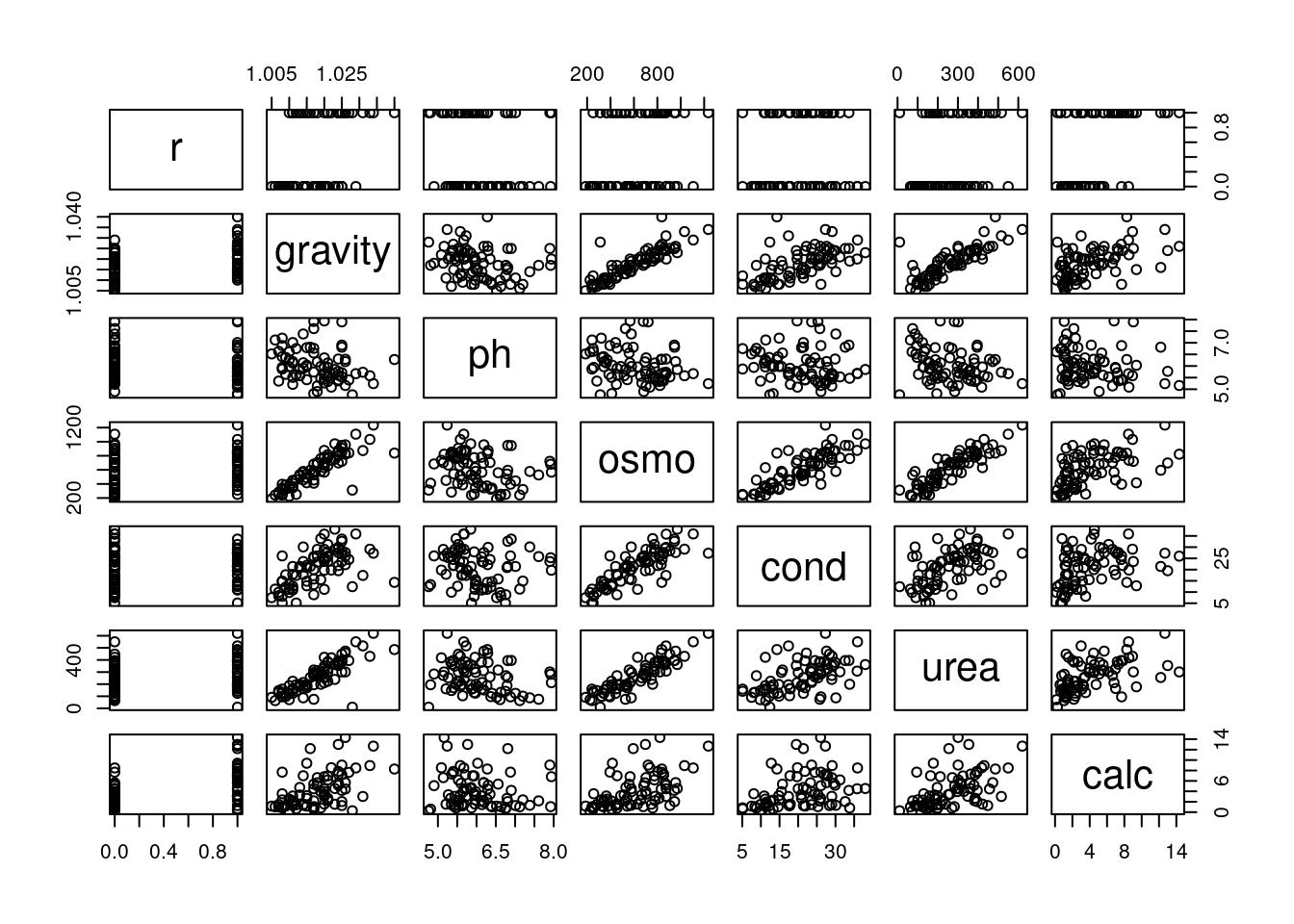
6 0 1.020 5.27 668 25.3 252 3.34dat = na.omit(urine)Let’s look at pairwise scatter plots of the seven variables.
pairs(dat)
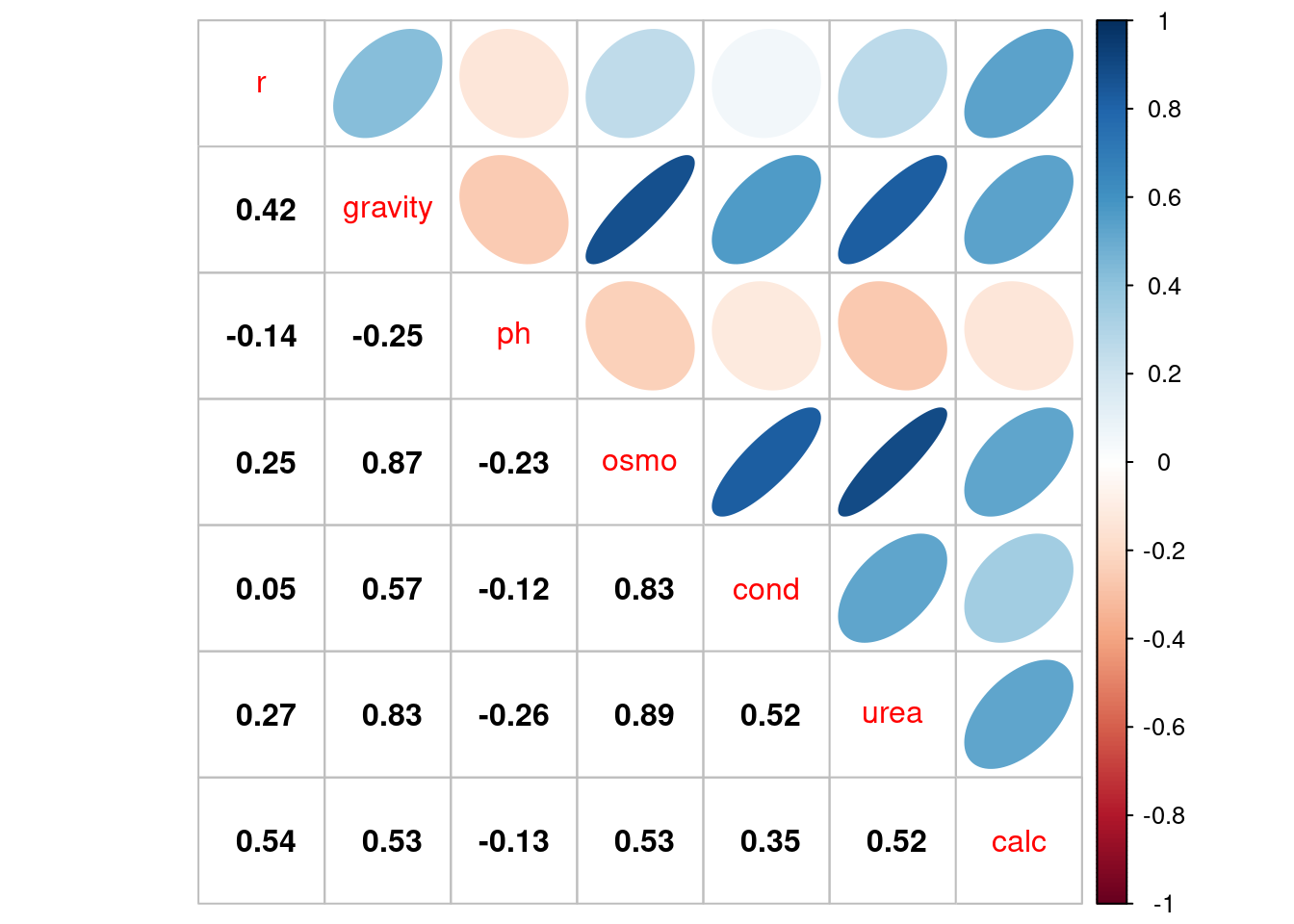
One thing that stands out is that several of these variables are strongly correlated with one another. For example gravity and osmo appear to have a very close linear relationship. Collinearity between x variables in linear regression models can cause trouble for statistical inference. Two correlated variables will compete for the ability to predict the response variable, leading to unstable estimates. This is not a problem for prediction of the response, if prediction is the end goal of the model. But if our objective is to discover how the variables relate to the response, we should avoid collinearity.
When two covariates are highly correlated we call this relation collinearity. When one covariate in a multiple regression model can be linearly predicted from the others with a substantial degree of accuracy we call this relation multicollinearity. It is possible that no two pairs of a such a group of covariates are correlated.
In both cases this will lead to the design matrix being almost singular. Near singular matrices are a strong cause of instability in numerical calculations. Statistical this tends to lead to a model with inflated standard errors compared to models where we only keep the a subset where variables are neither collinear nor multicollinear. A consequence of this is that we will see a drop in statistical significance for these variables, which will make interpreting the model harder.
We have seen a few strategies ways to deal with these issues:
pair plot in the exploratory data analysis phase.We can more formally estimate the correlation among these variables using the corrplot package.
library("corrplot")corrplot 0.95 loadedCor = cor(dat)
corrplot(Cor, type="upper", method="ellipse", tl.pos="d")
corrplot(Cor, type="lower", method="number", col="black",
add=TRUE, diag=FALSE, tl.pos="n", cl.pos="n")
One primary goal of this analysis is to find out which variables are related to the presence of calcium oxalate crystals. This objective is often called “variable selection.” We have already seen one way to do this: fit several models that include different sets of variables and see which one has the best DIC. Another way to do this is to use a linear model where the priors for the \beta coefficients favor values near 0 (indicating a weak relationship). This way, the burden of establishing association lies with the data. If there is not a strong signal, we assume it doesn’t exist.
Rather than tailoring a prior for each individual \beta based on the scale its covariate takes values on, it is customary to subtract the mean and divide by the standard deviation for each variable.
X = scale(dat[,-1], center=TRUE, scale=TRUE)
head(X[,"gravity"]) 2 3 4 5 6 7
-0.1403037 -1.3710690 -0.9608139 -1.7813240 0.2699514 -0.8240622 colMeans(X) gravity ph osmo cond urea
-9.861143e-15 8.511409e-17 1.515743e-16 -1.829852e-16 7.335402e-17
calc
-1.689666e-18 apply(X, 2, sd)gravity ph osmo cond urea calc
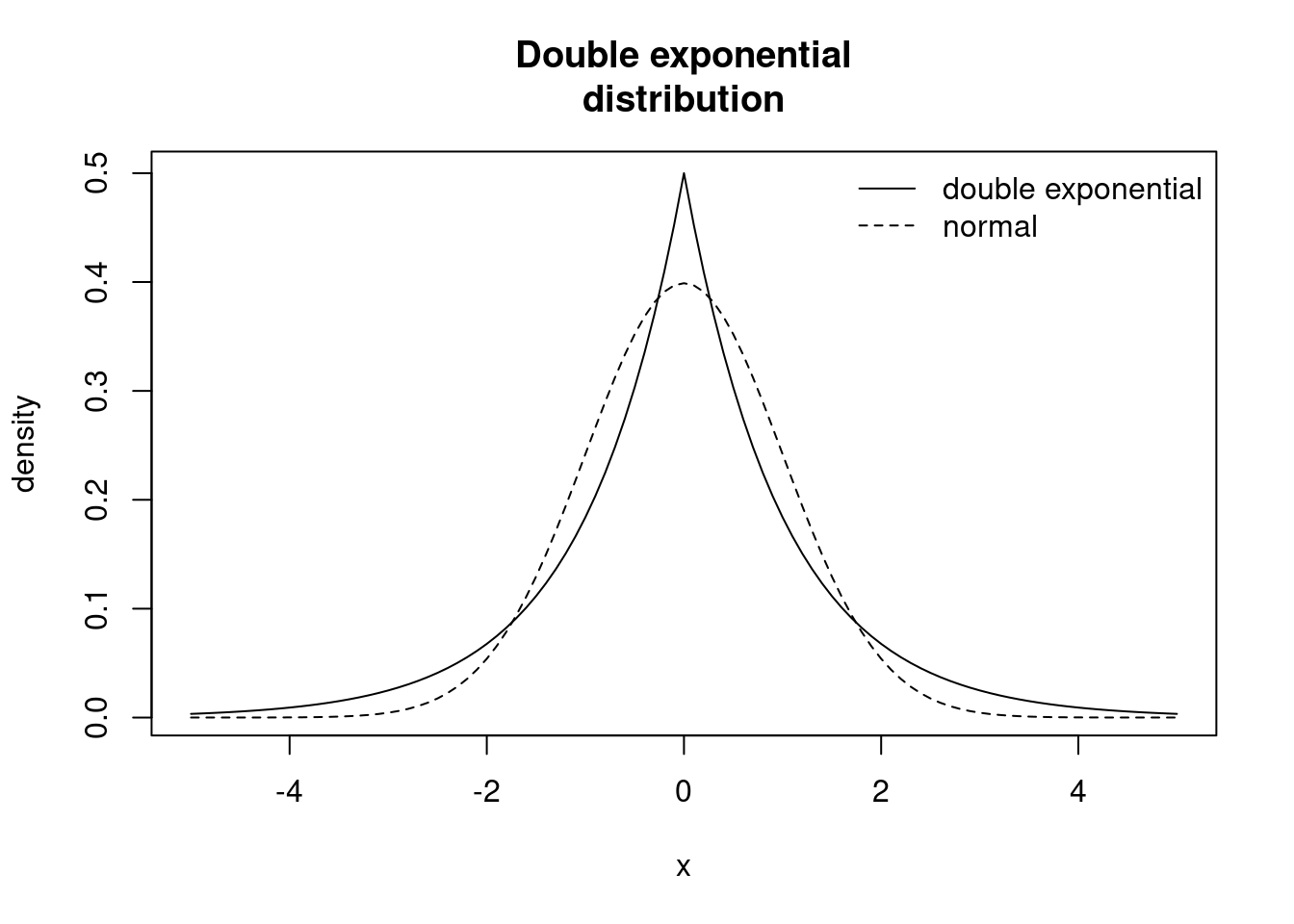
1 1 1 1 1 1 Our prior for the \beta (which we’ll call b in the model) coefficients will be the double exponential (or Laplace) distribution, which as the name implies, is the exponential distribution with tails extending in the positive direction as well as the negative direction, with a sharp peak at 0. We can read more about it in the JAGS manual. The distribution looks like:
ddexp = function(x, mu, tau) {
0.5*tau*exp(-tau*abs(x-mu))
}
curve(ddexp(x, mu=0.0, tau=1.0), from=-5.0, to=5.0,
ylab="density",
main="Double exponential\ndistribution") # double exponential distribution
curve(dnorm(x, mean=0.0, sd=1.0), from=-5.0, to=5.0,
lty=2, add=TRUE) # normal distribution
legend("topright",
legend=c("double exponential", "normal"),
lty=c(1,2), bty="n")
library("rjags")Loading required package: codaLinked to JAGS 4.3.2Loaded modules: basemod,bugsmod1_string =
" model {
for (i in 1:length(y)) {
y[i] ~ dbern(p[i])
logit(p[i]) = int + b[1]*gravity[i] +
b[2]*ph[i] +
b[3]*osmo[i] +
b[4]*cond[i] +
b[5]*urea[i] +
b[6]*calc[i]
}
int ~ dnorm(0.0, 1.0/25.0)
for (j in 1:6) {
b[j] ~ ddexp(0.0, sqrt(2.0)) # has var 1.0
}
} "
set.seed(92)
head(X) gravity ph osmo cond urea calc
2 -0.1403037 -0.4163725 -0.1528785 -0.1130908 0.25747827 0.09997564
3 -1.3710690 1.6055972 -1.2218894 -0.7502609 -1.23693077 -0.54608444
4 -0.9608139 -0.7349020 -0.8585927 -1.0376121 -0.29430353 -0.60978050
5 -1.7813240 0.6638579 -1.7814497 -1.6747822 -1.31356713 -0.91006194
6 0.2699514 -1.0672806 0.2271214 0.5490664 -0.07972172 -0.24883614
7 -0.8240622 -0.5825618 -0.6372741 -0.4379226 -0.51654898 -0.83726644data_jags = list(y=dat$r,
gravity=X[,"gravity"],
ph=X[,"ph"],
osmo=X[,"osmo"],
cond=X[,"cond"],
urea=X[,"urea"],
calc=X[,"calc"])
params = c("int", "b")
mod1 = jags.model(textConnection(mod1_string), data=data_jags, n.chains=3)Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph information:
Observed stochastic nodes: 77
Unobserved stochastic nodes: 7
Total graph size: 1085
Initializing modelupdate(mod1, 1e3)
mod1_sim = coda.samples(model=mod1,
variable.names=params,
n.iter=5e3)
mod1_csim = as.mcmc(do.call(rbind, mod1_sim))
## convergence diagnostics
par(mar = c(2.5, 1, 2.5, 1))
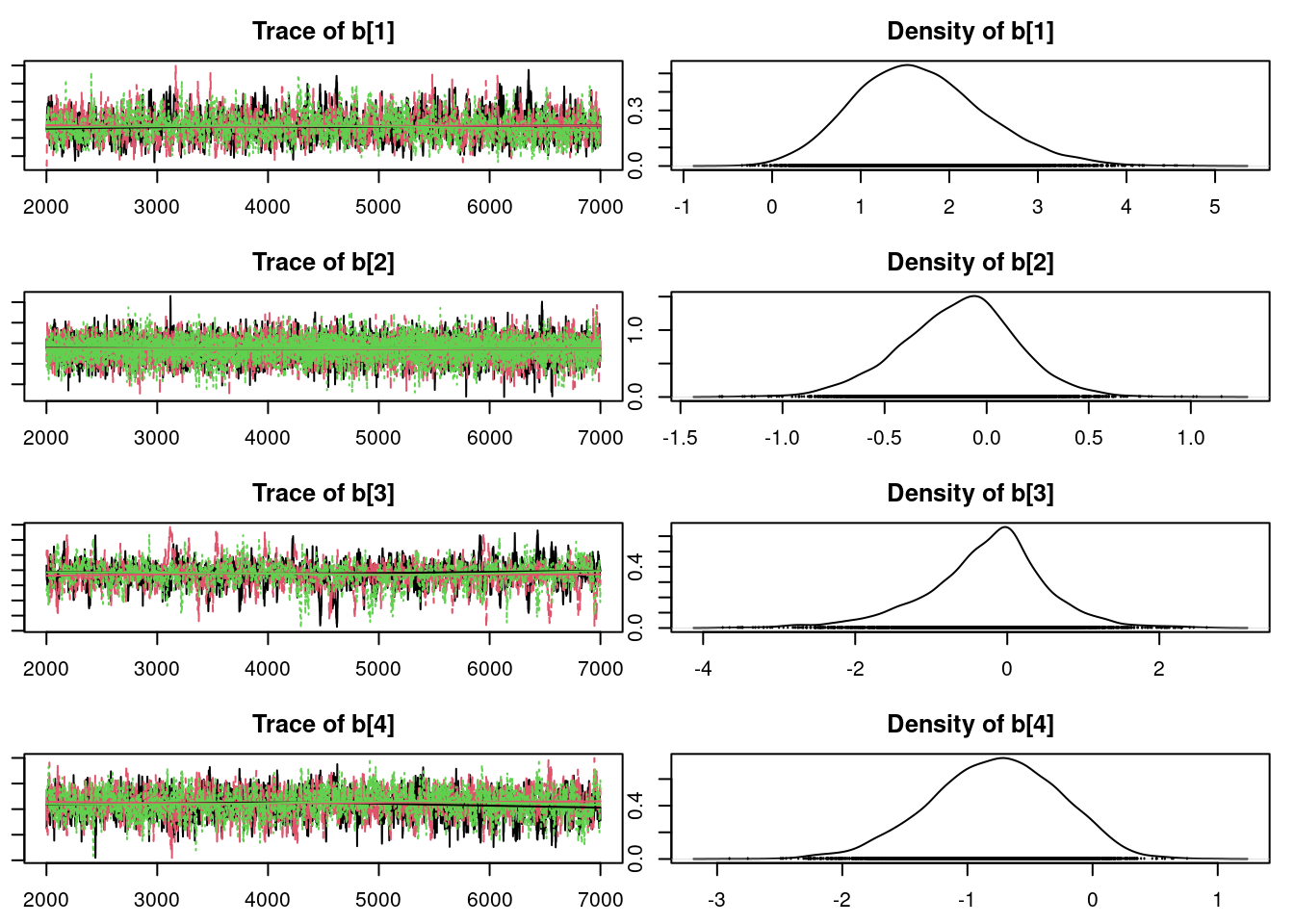
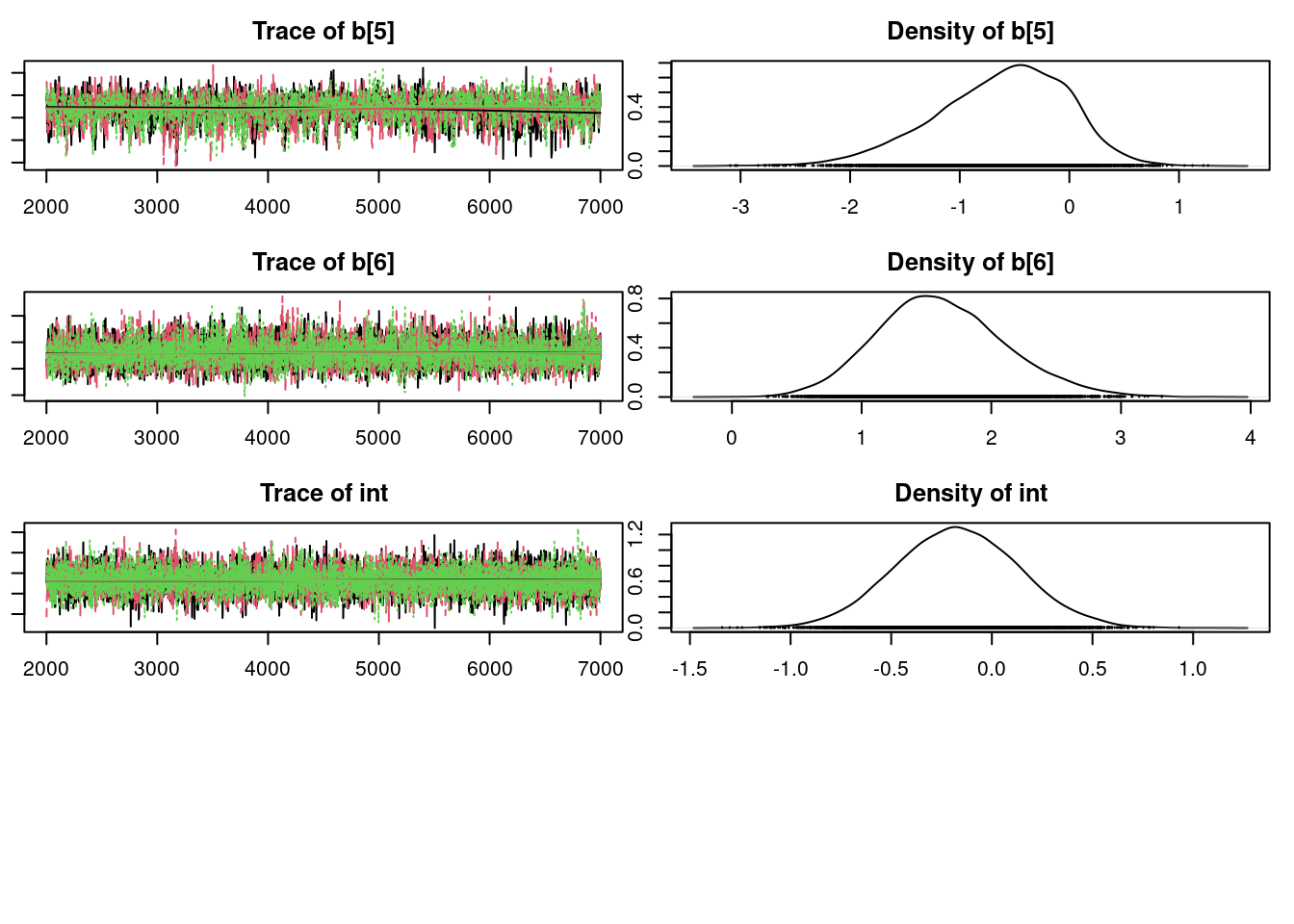
plot(mod1_sim, ask=TRUE)
gelman.diag(mod1_sim)Potential scale reduction factors:
Point est. Upper C.I.
b[1] 1 1.01
b[2] 1 1.00
b[3] 1 1.01
b[4] 1 1.01
b[5] 1 1.01
b[6] 1 1.00
int 1 1.00
Multivariate psrf
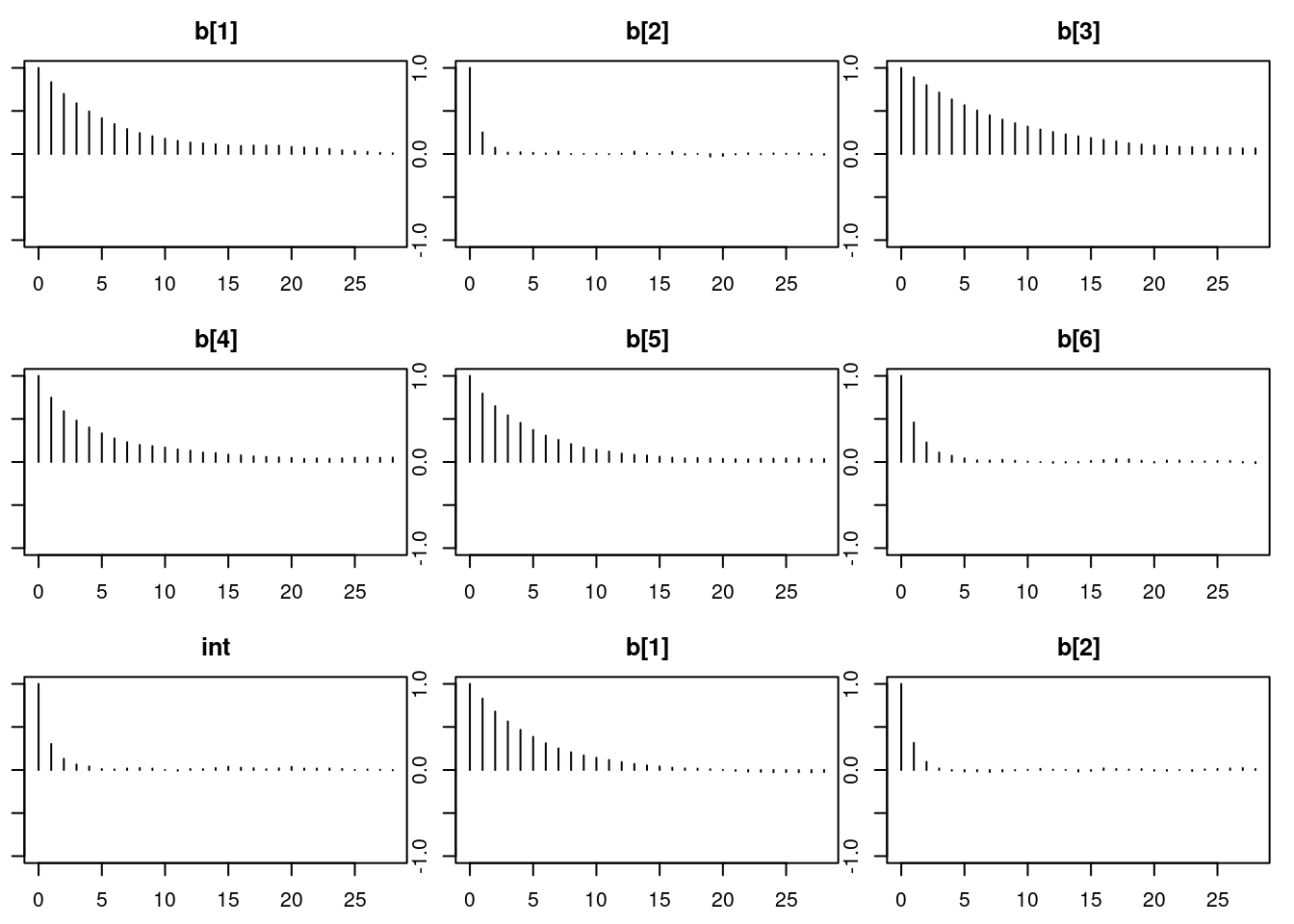
1autocorr.diag(mod1_sim) b[1] b[2] b[3] b[4] b[5] b[6]
Lag 0 1.00000000 1.000000000 1.00000000 1.00000000 1.00000000 1.00000000
Lag 1 0.83139527 0.282140123 0.89937587 0.75981398 0.79178141 0.48729555
Lag 5 0.40470384 -0.006327089 0.58956682 0.36469706 0.36883565 0.06484881
Lag 10 0.17463933 0.005297018 0.34396080 0.19057429 0.16280890 0.01297326
Lag 50 -0.02257132 0.005922485 0.03869131 0.02883672 0.01546907 0.01094675
int
Lag 0 1.000000000
Lag 1 0.292404424
Lag 5 0.027938430
Lag 10 -0.005587174
Lag 50 -0.024954679autocorr.plot(mod1_sim)
effectiveSize(mod1_sim) b[1] b[2] b[3] b[4] b[5] b[6] int
1381.6646 8406.5088 781.1091 1460.5169 1467.1893 4620.9686 7352.8806 ## calculate DIC
dic1 = dic.samples(mod1, n.iter=1e3)Let’s look at the results.
summary(mod1_sim)
Iterations = 2001:7000
Thinning interval = 1
Number of chains = 3
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
b[1] 1.7152 0.7790 0.006360 0.022276
b[2] -0.1446 0.2875 0.002348 0.003120
b[3] -0.2905 0.8612 0.007032 0.032268
b[4] -0.7802 0.5209 0.004253 0.014612
b[5] -0.6468 0.6256 0.005108 0.017049
b[6] 1.6097 0.4990 0.004074 0.007142
int -0.1786 0.3096 0.002528 0.003542
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
b[1] 0.3724 1.1671 1.6583 2.19458 3.4378
b[2] -0.7508 -0.3280 -0.1261 0.04550 0.3916
b[3] -2.1719 -0.7578 -0.1949 0.20984 1.3341
b[4] -1.8543 -1.1241 -0.7660 -0.41575 0.1720
b[5] -2.0291 -1.0392 -0.5778 -0.18852 0.3953
b[6] 0.7134 1.2605 1.5821 1.92323 2.6894
int -0.7691 -0.3883 -0.1815 0.02756 0.4411#par(mfrow=c(3,2))
par(mar = c(2.5, 1, 2.5, 1))
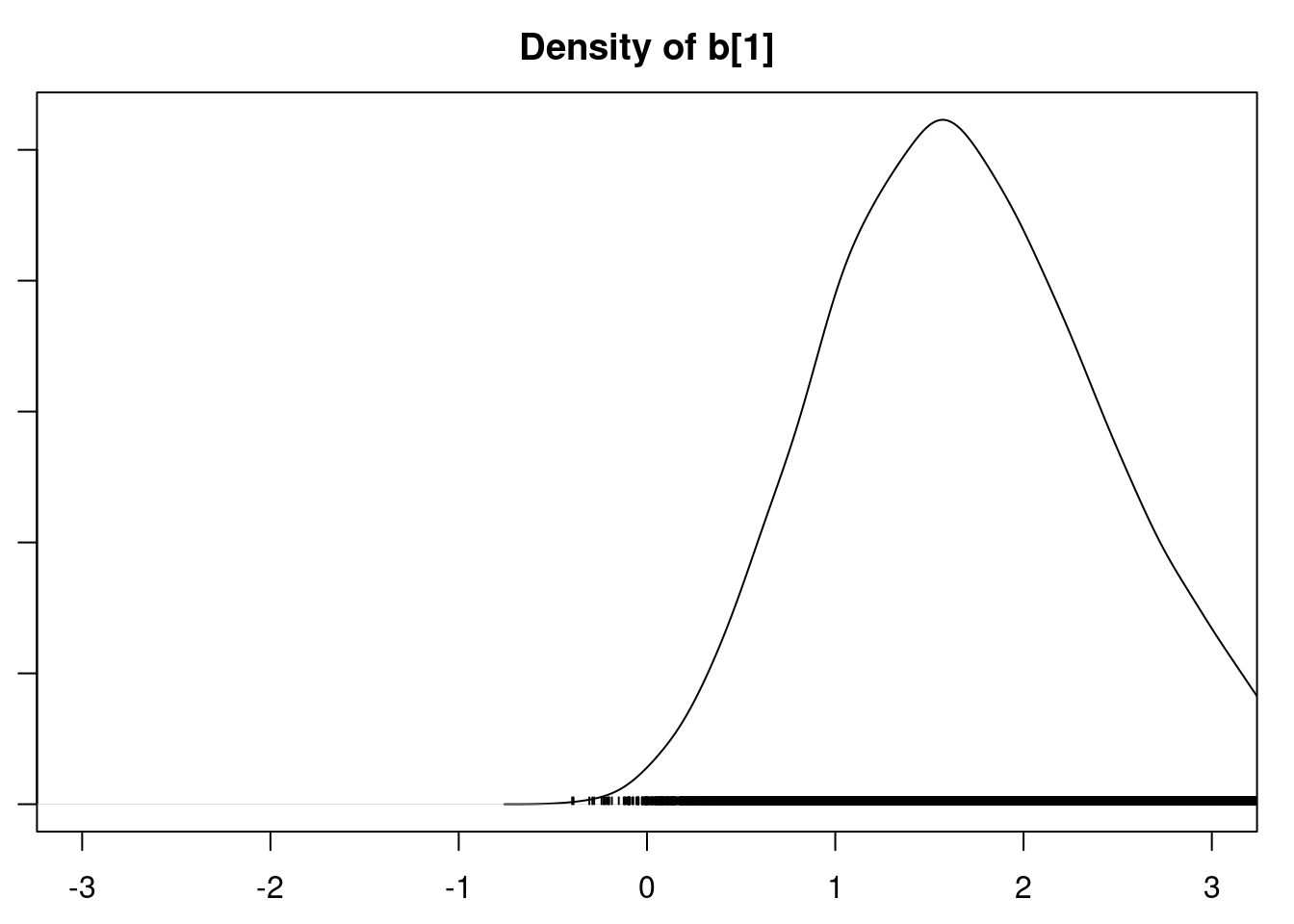
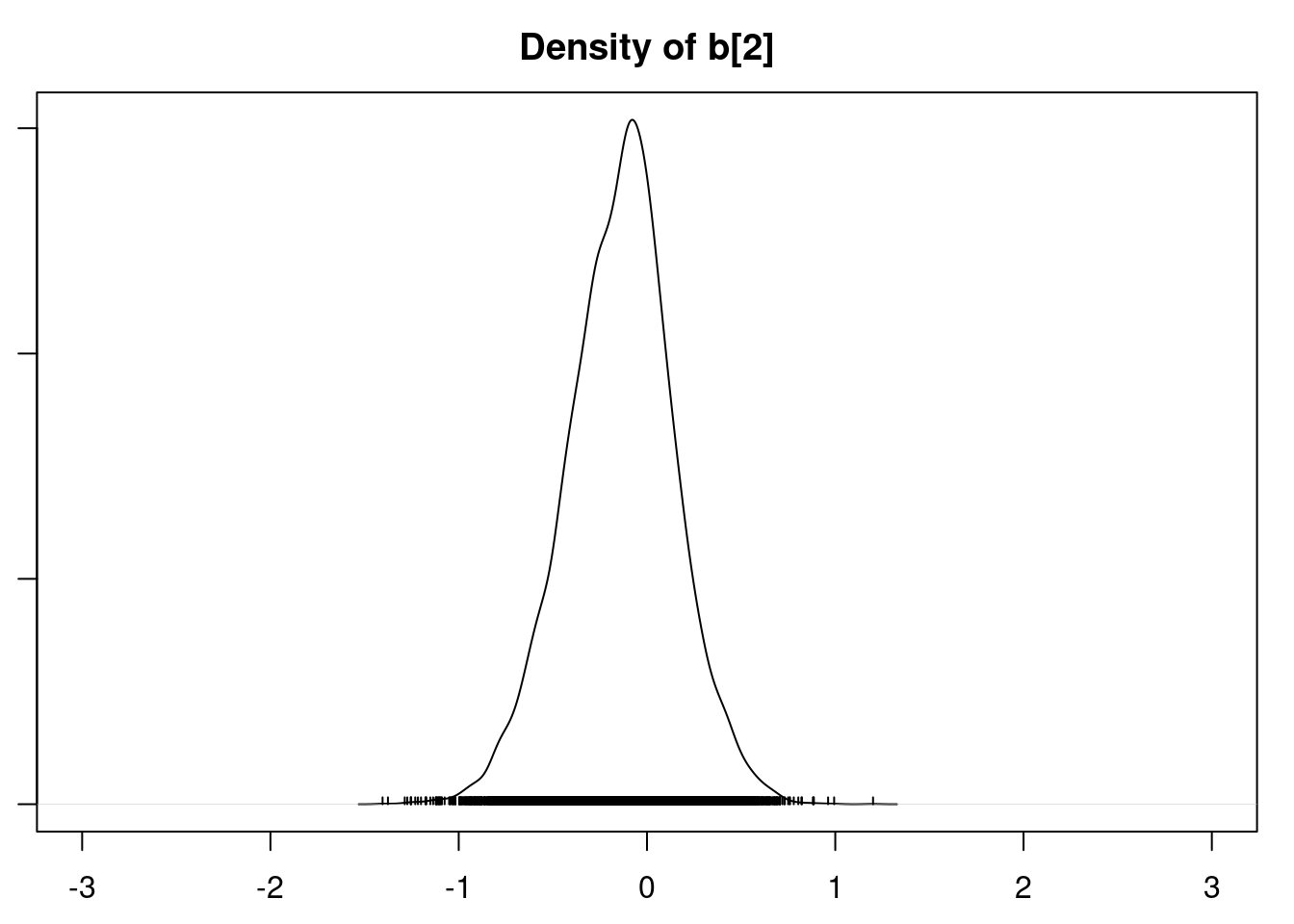
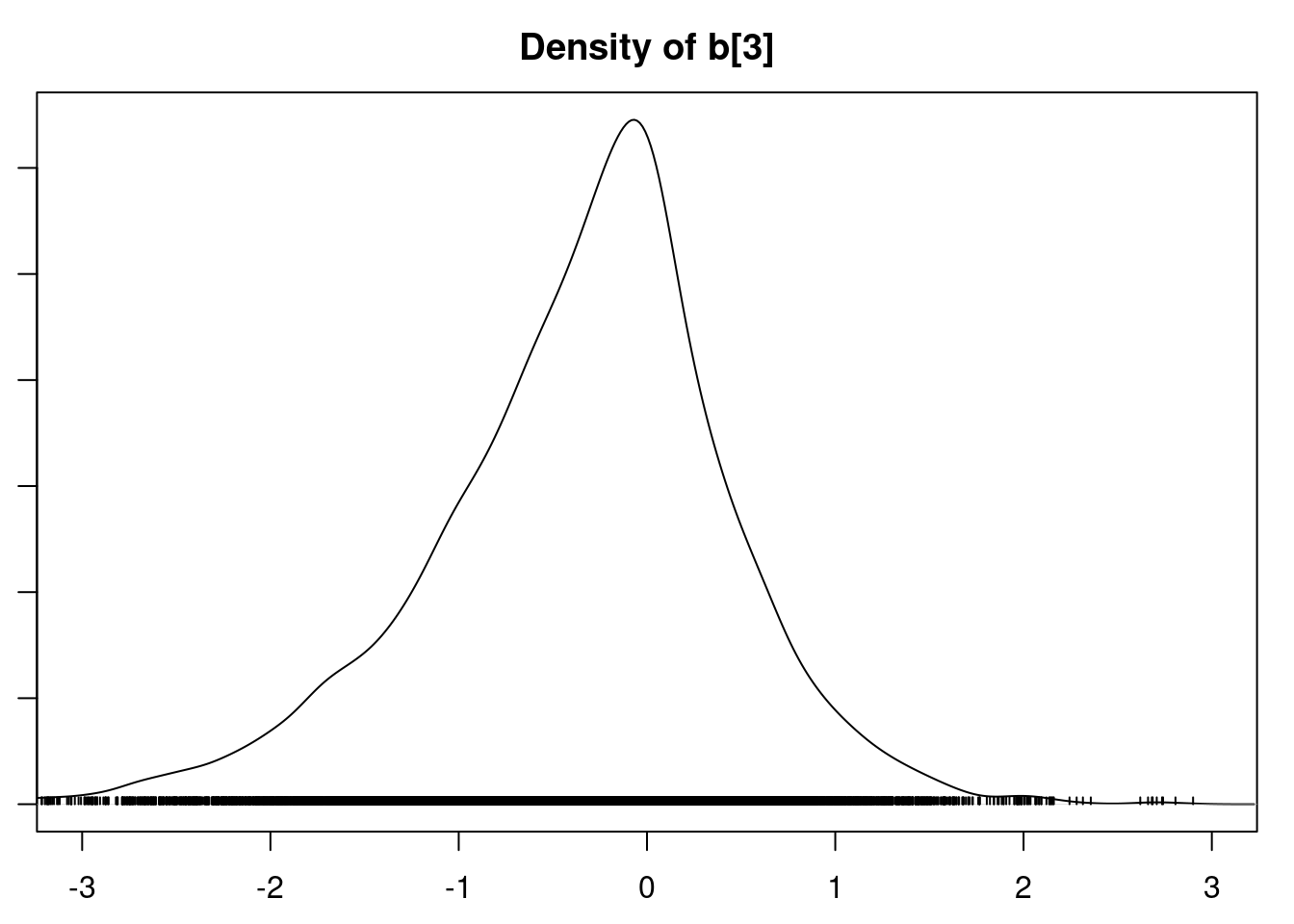
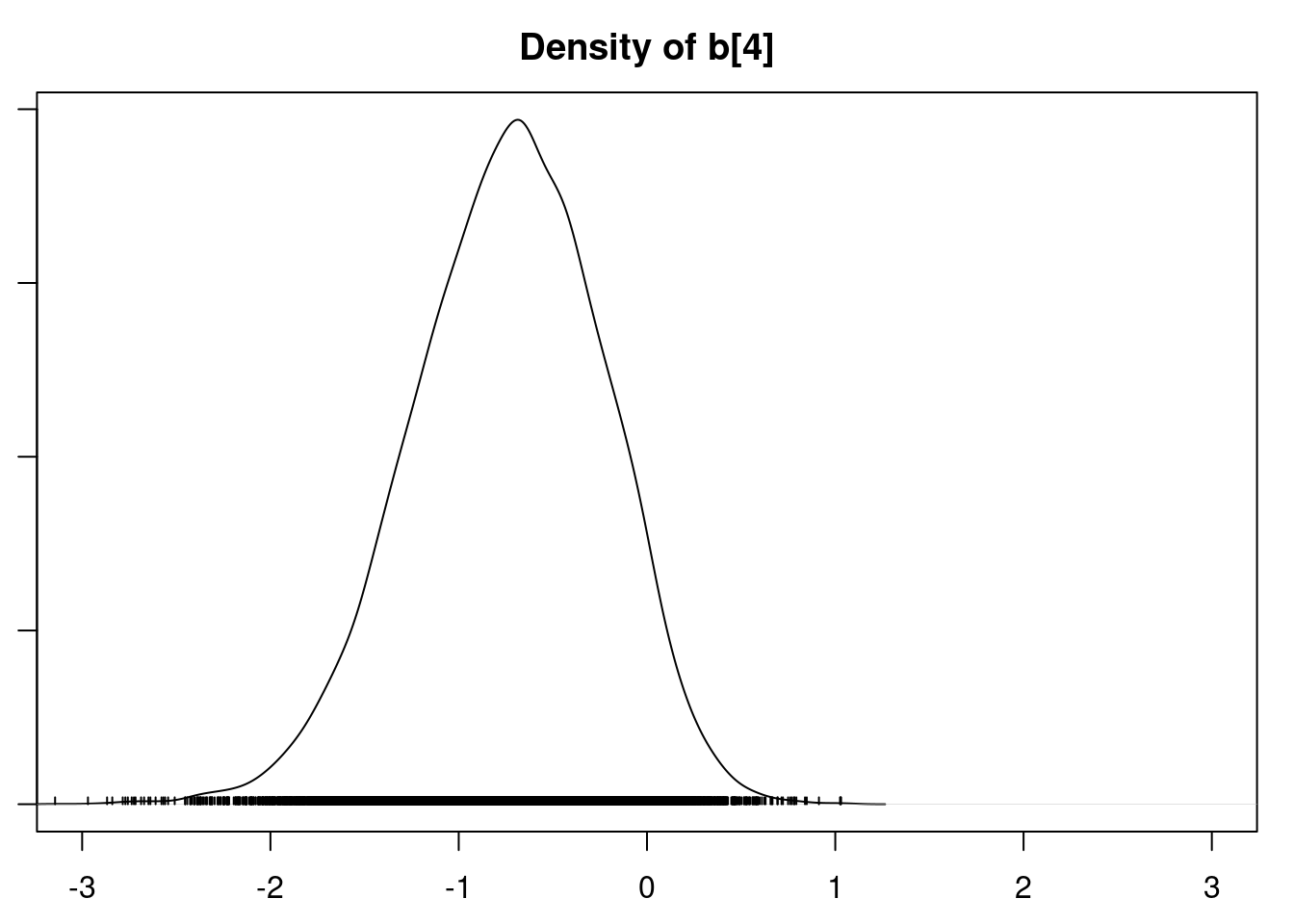
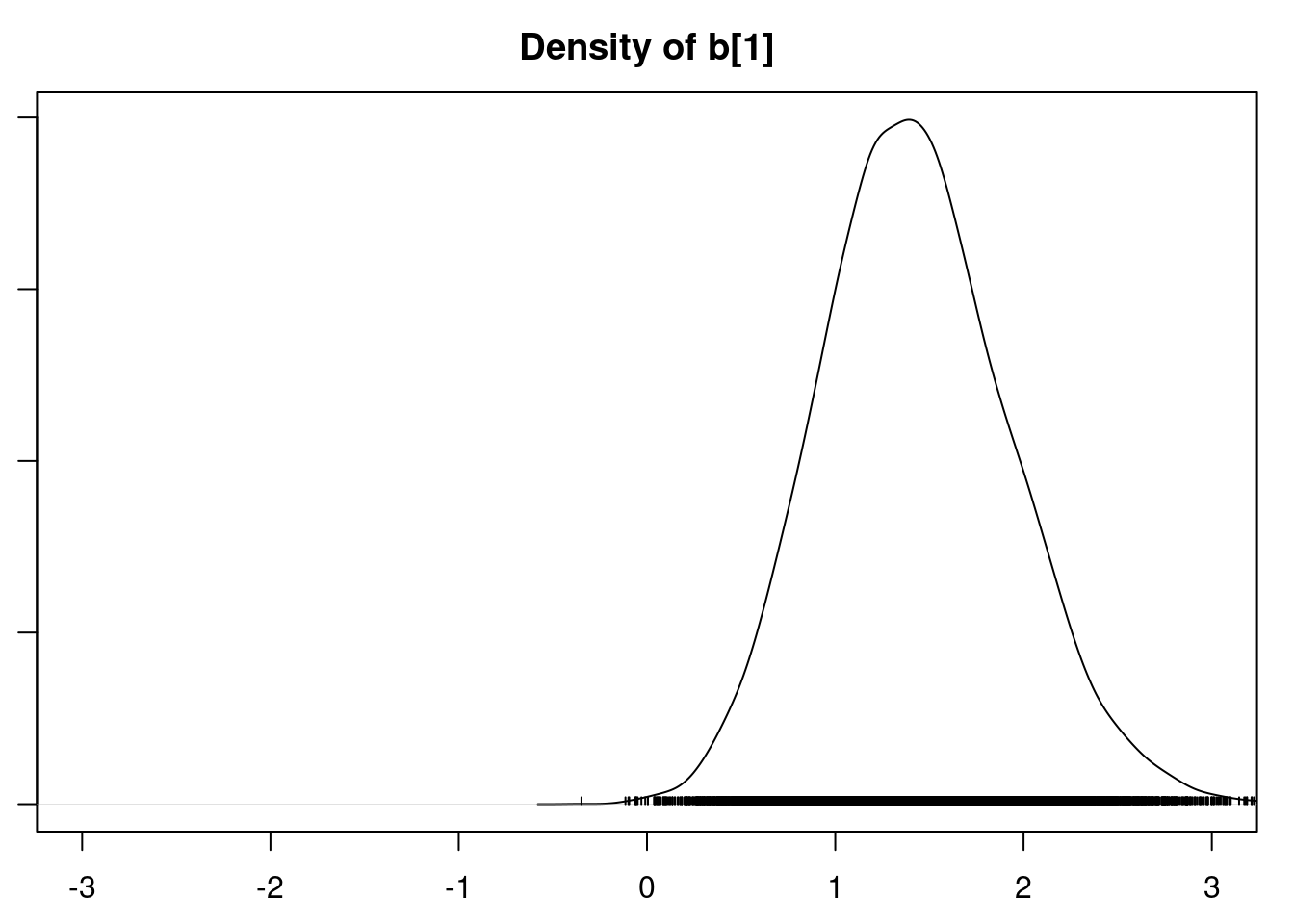
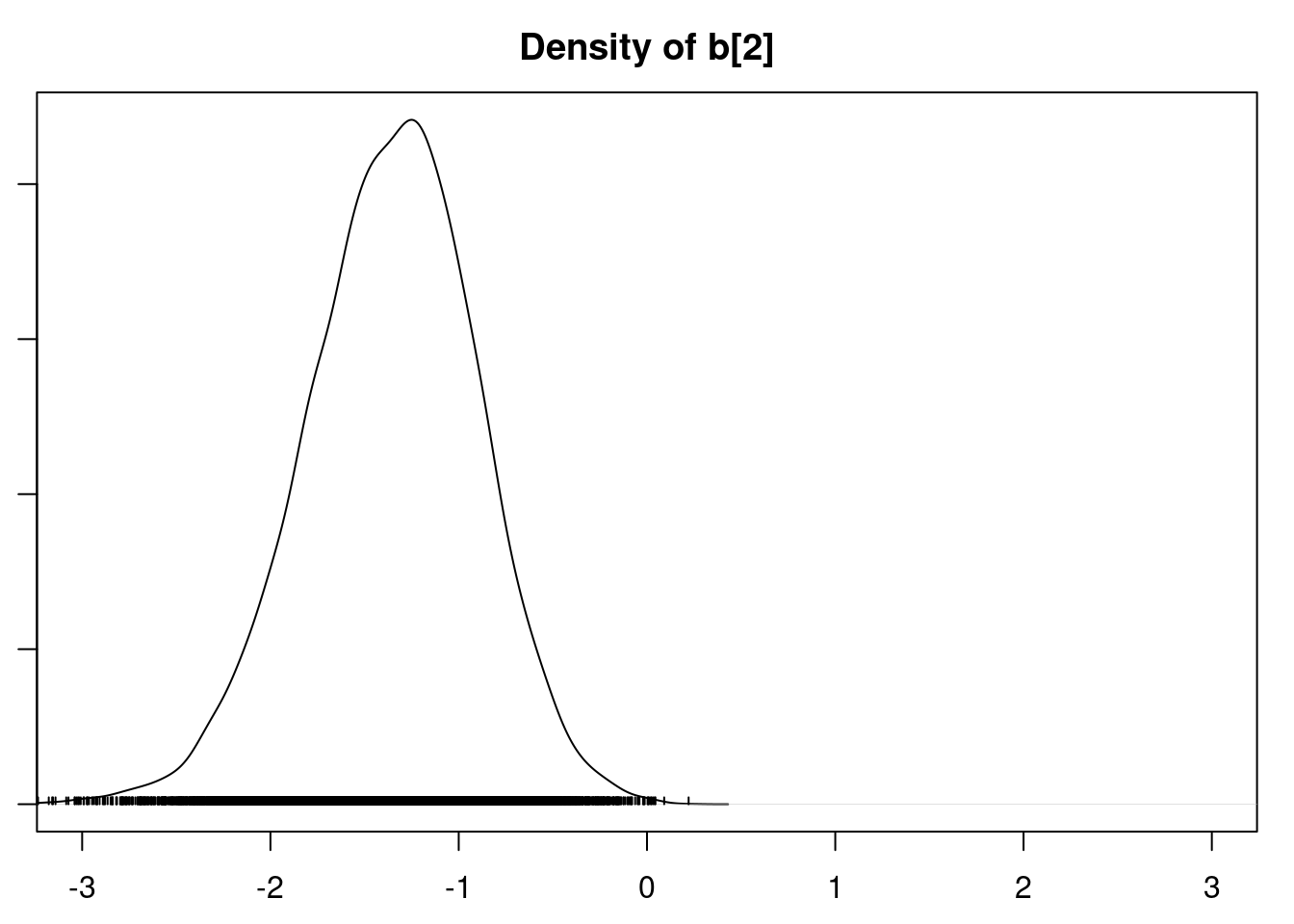
densplot(mod1_csim[,1:6], xlim=c(-3.0, 3.0))
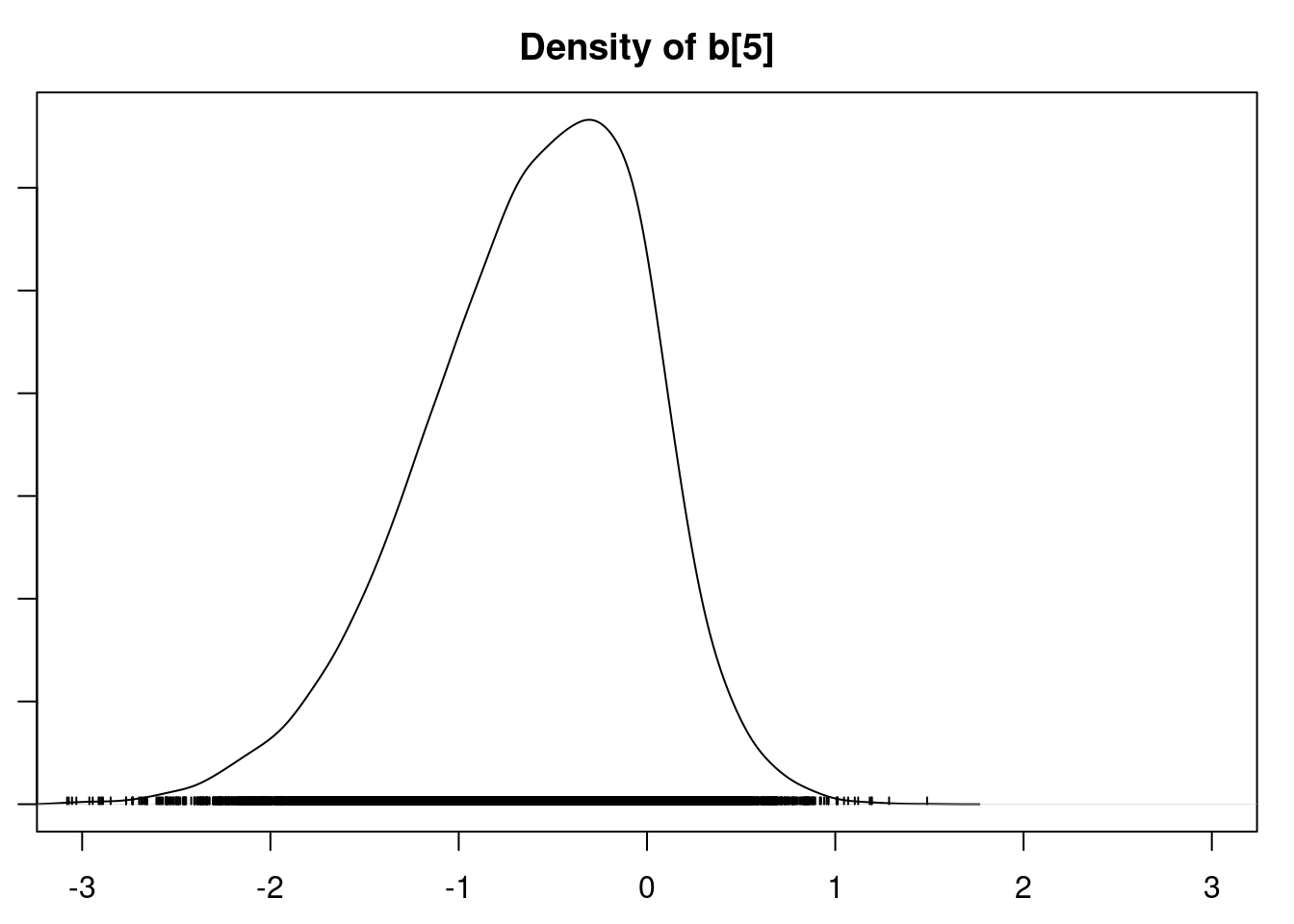
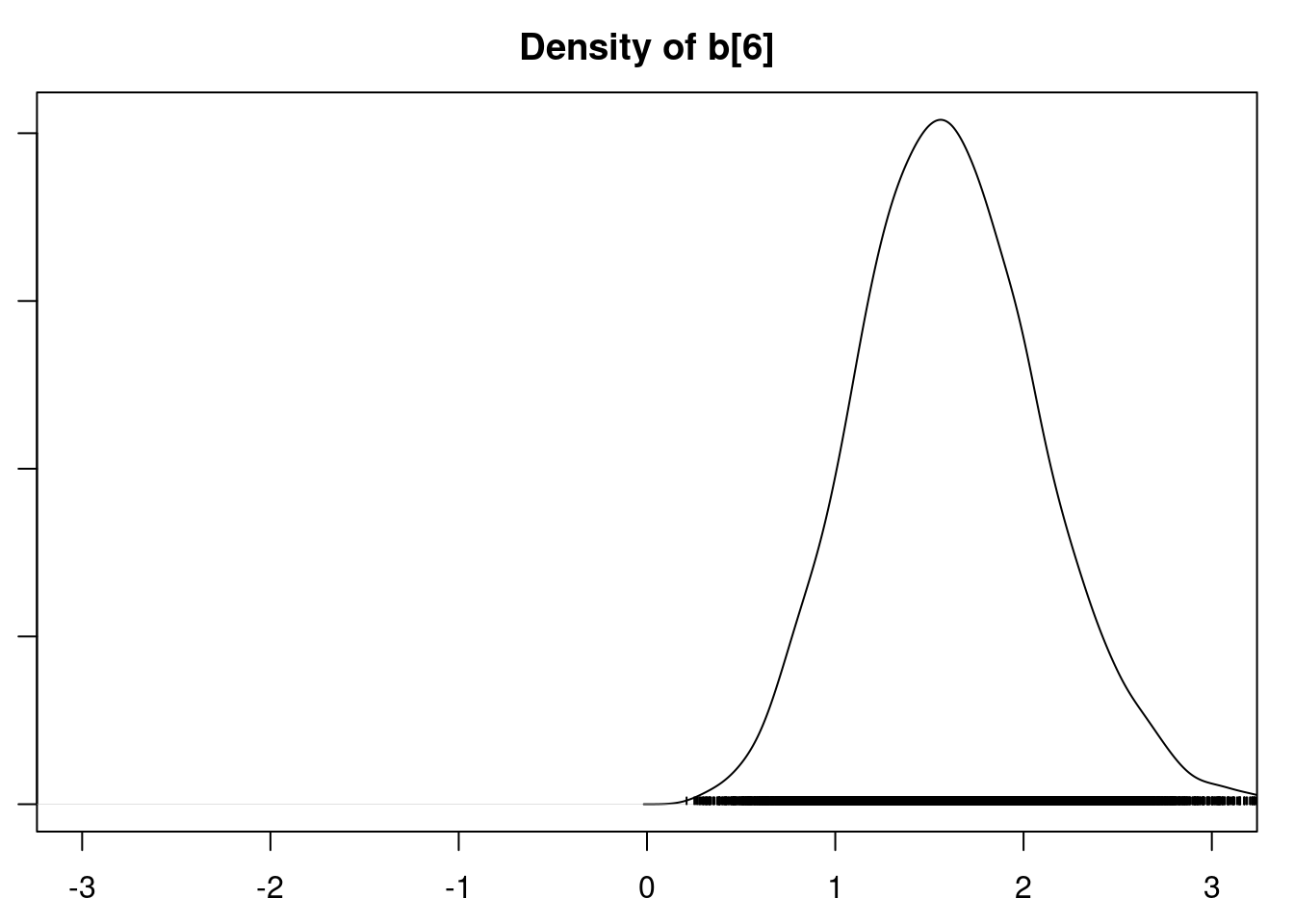
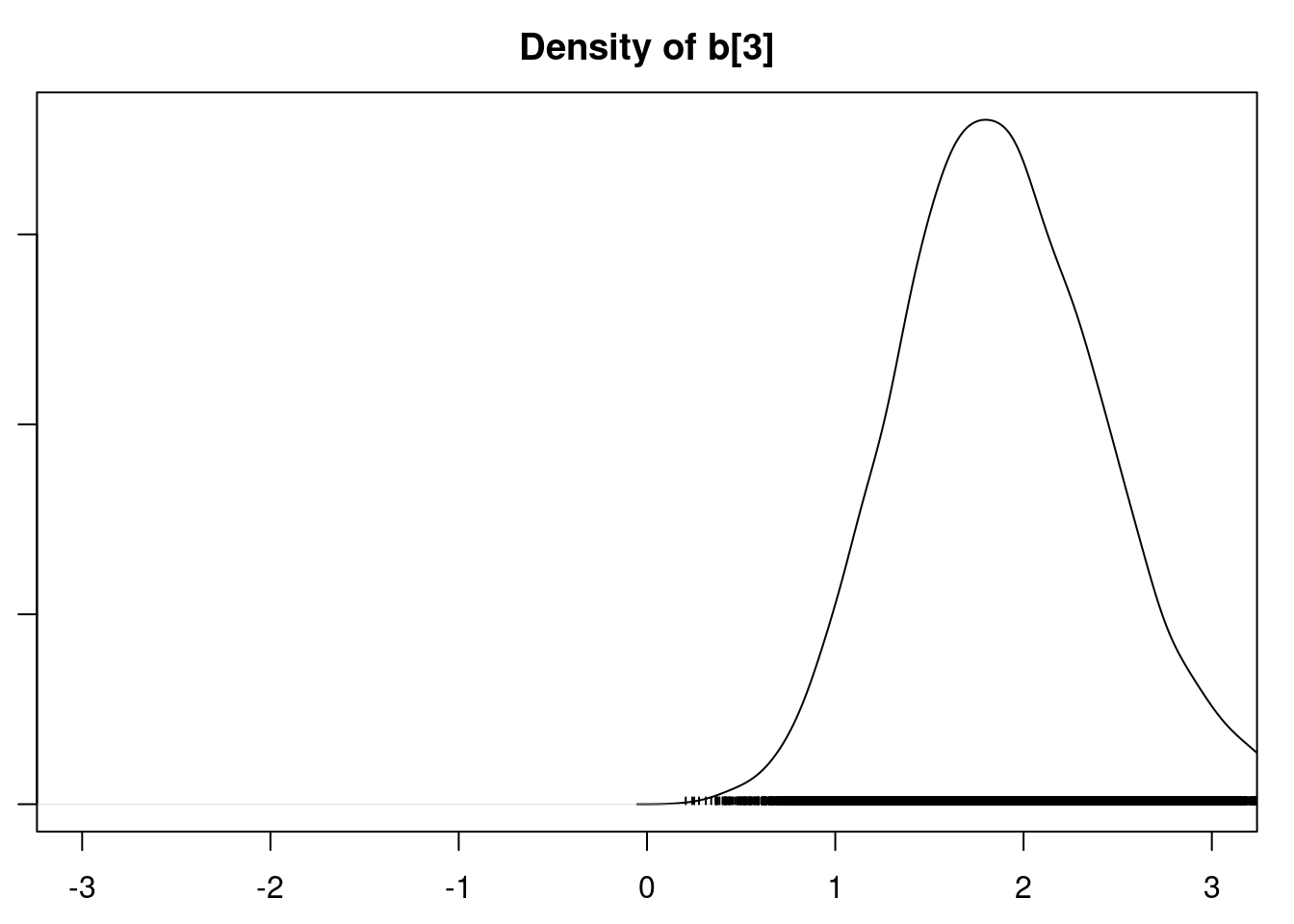
colnames(X) # variable names[1] "gravity" "ph" "osmo" "cond" "urea" "calc" It is clear that the coefficients for variables gravity, cond (conductivity), and calc (calcium concentration) are not 0. The posterior distribution for the coefficient of osmo (osmolarity) looks like the prior, and is almost centered on 0 still, so we’ll conclude that osmo is not a strong predictor of calcium oxalate crystals. The same goes for ph.
urea (urea concentration) appears to be a borderline case. However, if we refer back to our correlations among the variables, we see that urea is highly correlated with gravity, so we opt to remove it.
Our second model looks like this:
mod2_string = " model {
for (i in 1:length(y)) {
y[i] ~ dbern(p[i])
logit(p[i]) = int + b[1]*gravity[i] + b[2]*cond[i] + b[3]*calc[i]
}
int ~ dnorm(0.0, 1.0/25.0)
for (j in 1:3) {
b[j] ~ dnorm(0.0, 1.0/25.0) # noninformative for logistic regression
}
} "
mod2 = jags.model(textConnection(mod2_string), data=data_jags, n.chains=3)Warning in jags.model(textConnection(mod2_string), data = data_jags, n.chains =
3): Unused variable "ph" in dataWarning in jags.model(textConnection(mod2_string), data = data_jags, n.chains =
3): Unused variable "osmo" in dataWarning in jags.model(textConnection(mod2_string), data = data_jags, n.chains =
3): Unused variable "urea" in dataCompiling model graph
Resolving undeclared variables
Allocating nodes
Graph information:
Observed stochastic nodes: 77
Unobserved stochastic nodes: 4
Total graph size: 635
Initializing modelupdate(mod2, 1e3)
mod2_sim = coda.samples(model=mod2,
variable.names=params,
n.iter=5e3)
mod2_csim = as.mcmc(do.call(rbind, mod2_sim))
par(mar = c(2.5, 1, 2.5, 1))
#plot(mod2_sim, ask=TRUE)
plot(mod2_sim)
gelman.diag(mod2_sim)Potential scale reduction factors:
Point est. Upper C.I.
b[1] 1 1
b[2] 1 1
b[3] 1 1
int 1 1
Multivariate psrf
1autocorr.diag(mod2_sim) b[1] b[2] b[3] int
Lag 0 1.000000000 1.0000000000 1.0000000000 1.000000000
Lag 1 0.583627533 0.6720443263 0.4990170960 0.284711480
Lag 5 0.114789188 0.1788950472 0.0546211037 0.002815859
Lag 10 0.010922205 0.0126509977 -0.0005439148 0.000864474
Lag 50 0.001713864 0.0006537317 -0.0011842400 0.004314294autocorr.plot(mod2_sim)
effectiveSize(mod2_sim) b[1] b[2] b[3] int
3518.752 2665.977 4500.056 8353.729 dic2 = dic.samples(mod2, n.iter=1e3)dic1Mean deviance: 68.53
penalty 5.573
Penalized deviance: 74.1 dic2Mean deviance: 71.23
penalty 4.095
Penalized deviance: 75.33 summary(mod2_sim)
Iterations = 2001:7000
Thinning interval = 1
Number of chains = 3
Sample size per chain = 5000
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
b[1] 1.3960 0.5052 0.004125 0.008532
b[2] -1.3296 0.4619 0.003772 0.008955
b[3] 1.8637 0.5514 0.004502 0.008238
int -0.1536 0.3217 0.002627 0.003523
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
b[1] 0.4794 1.0393 1.372 1.72259 2.4580
b[2] -2.2829 -1.6280 -1.314 -1.00698 -0.4713
b[3] 0.8744 1.4785 1.832 2.21421 3.0297
int -0.7783 -0.3713 -0.156 0.06063 0.4745HPDinterval(mod2_csim) lower upper
b[1] 0.4008897 2.3673187
b[2] -2.2333234 -0.4259612
b[3] 0.7789707 2.9103415
int -0.7745084 0.4776574
attr(,"Probability")
[1] 0.95#par(mfrow=c(3,1))
par(mar = c(2.5, 1, 2.5, 1))
densplot(mod2_csim[,1:3], xlim=c(-3.0, 3.0))
colnames(X)[c(1,4,6)] # variable names[1] "gravity" "cond" "calc" The DIC is actually better for the first model. Note that we did change the prior between models, and generally we should not use the DIC to choose between priors. Hence comparing DIC between these two models may not be a fair comparison. Nevertheless, they both yield essentially the same conclusions. Higher values of gravity and calc (calcium concentration) are associated with higher probabilities of calcium oxalate crystals, while higher values of cond (conductivity) are associated with lower probabilities of calcium oxalate crystals.
There are more modeling options in this scenario, perhaps including transformations of variables, different priors, and interactions between the predictors, but we’ll leave it to you to see if you can improve the model.