## simulate data
y=c(-1,0,1)
T.all=400
for (i in 4:T.all) {
set.seed(i)
U=runif(1)
if(U<=0.5){
y.new=rnorm(1,0.1*y[i-1]+0.1*y[i-2],0.25)
}else if(U>0.8){
y.new=rnorm(1,0.3*y[i-1]+0.5*y[i-2],0.25)
}else{
y.new=rnorm(1,0.4*y[i-1]-0.5*y[i-2],0.25)
}
y=c(y,y.new)
}
plot(y,type='l',xlab='Time',ylab='Simulated Time Series')In this part, we will extend the location mixture of AR models to the location and scale mixture of AR models. We will show the derivation of the Gibbs sampler for the model parameters as well as the R code for the full posterior inference.
112.0.1 The Model
The location and scale mixture of AR(p) model for the data can be written hierarchically as follows:
\begin{aligned} &y_t\sim\sum_{k=1}^K\omega_kN(\mathbf{f}^T_t\boldsymbol{\beta}_k,\nu_k),\quad \mathbf{f}^T_t=(y_{t-1},\cdots,y_{t-p})^T,\quad t=p+1,\cdots,T\\ &\omega_k\sim Dir(a_1,\cdots,a_k),\quad \boldsymbol{\beta}_k\sim N(\mathbf{m}_0,\nu_k\mathbf{C}_0),\quad \nu_k\sim IG(\frac{n_0}{2},\frac{d_0}{2}) \end{aligned} \tag{112.1}
Introducing latent configuration variable L_t \in \{1,2,\cdots,K\}, such that L_t=k \iff y_t\sim N(\mathbf{f}^T_t\boldsymbol{\beta}_k,\nu_k), and denote \boldsymbol{\beta}=(\beta_1,\cdots,\beta_K), \boldsymbol{\omega}=(\omega_1,\cdots,\omega_K), \mathbf{L}=(L_1,\cdots,L_T), we can write the full posterior distribution as:
p(\boldsymbol{\beta},\boldsymbol{\nu},\boldsymbol{\omega},\mathbf{L}|\mathbf{Y},\mathbf{F}) \propto p(\mathbf{Y}|\boldsymbol{\beta},\boldsymbol{\nu},\boldsymbol{\omega},\mathbf{F})p(\boldsymbol{\beta})p(\boldsymbol{\nu})p(\boldsymbol{\omega})p(\mathbf{L}) we can write the full posterior distribution as \begin{aligned} p(\boldsymbol{\omega},\boldsymbol{\beta},\nu,\mathbf{L}|\mathbf{y})&\propto p(\mathbf{y}|\boldsymbol{\omega},\boldsymbol{\beta},\nu,\mathbf{L})p(\mathbf{L}|\boldsymbol{\omega})p(\boldsymbol{\omega})p(\boldsymbol{\beta})p(\nu)\\ &\propto \prod_{k=1}^K\prod_{\{t:L_t=k\}}N(y_t\mid\mathbf{f}^T_t\boldsymbol{\beta}_k,\nu)\prod_{k=1}^K\omega_k^{\sum_{t=1}^T\mathbf{1}(L_t=k)}\prod_{k=1}^K\omega_k^{a_k-1}\prod_{k=1}^K(N(\boldsymbol{\beta}_k\mid\mathbf{m}_0,\mathbf{C}_0)IG(\nu_k|\frac{n_0}{2},\frac{d_0}{2})) \end{aligned}
1.For \boldsymbol{\omega}, we have :
\boldsymbol{\omega}\mid \cdots\sim Dir(a_1+\sum_{t=1}^T\mathbf{1}(L_t=1),\cdots,a_K+\sum_{t=1}^T\mathbf{1}(L_t=K))
- For L_t we have
p(L_t=k\mid\cdots)\propto \omega_kN(y_t\mid\mathbf{f}^T_t\boldsymbol{\beta}_k,\nu)
Therefore, L_t follows a discrete distribution on \{1,\cdots,K\}. with probability that L_t taking k proportional to \omega_k N(y_t\mid\mathbf{f}^T_t\boldsymbol{\beta}_k,\nu).
- For ν_k and \boldsymbol{\beta}_k denote \mathbf{\tilde{y}}_k:= \{y_t: L_t=k\} and \mathbf{\tilde{F}}_k as the design matrix belonging to \mathbf{\tilde{y}}_k, and n_l=\sum_{}^{T}\mathbb{1}(L_t=k), we have \nu_k\mid \cdots \sim \mathcal{IG}(\frac{n_k^*}{2},\frac{d_k^*}{2}) and \boldsymbol{\beta}_k \sim \mathcal{N}(\mathbf{m}_k,\nu_k\mathbf{C}_k) , where \begin{aligned} \mathbf{e}_k &= \mathbf{\tilde{y}}_k-\mathbf{\tilde{F}}_k^T\mathbf{m}_0, &\mathbf{Q}_k &= \mathbf{\tilde{F}}_k^T\mathbf{C}_0\mathbf{\tilde{F}}_k+\mathbf{I}_{n_k}, &\mathbf{A}_k &= \mathbf{C}_0\mathbf{\tilde{F}}_k\mathbf{Q}_k^{-1} \\ \mathbf{m}_k &= \mathbf{m}_0+\mathbf{A}_k\mathbf{e}_k, &\mathbf{C}_k &= \mathbf{C}_0-\mathbf{A}_k\mathbf{Q}_k\mathbf{A}_k^{T} \\ n_k^* &= n_0+n_k, &d_k^* &= d_0+\mathbf{e}_k^T\mathbf{Q}_k^{-1}\mathbf{e}_k \end{aligned}
Now we have the full conditional distributions for all model parameters. We proceed to implement the model in R with a simulate dataset.
112.0.2 Step 1 Simulate data
We generate some data from the three component mixture of AR(2) process.
Given y_1=-1 and y_2=0 we generate y_3 to y_{3:200} from the following distribution:
\begin{aligned} y_i \sim 0.5\ \mathcal{N}(0.1 y_{t-1} + 0.1 y_{t-2}, 0.25) \\ +\ 0.3\ \mathcal{N}(0.4 y_{t-1} - 0.5 y_{t-2}, 0.25) \\ +\ 0.2\ \mathcal{N}(0.3 y_{t-1} + 0.5 y_{t-2}, 0.25) \end{aligned}
112.0.3 Setting the Prior
We will fit a location and scale mixture of AR(2) models using 3 components. That is, p=2 and K=3. Firstly, we set up the model by choosing prior hyperparameters. We use weakly informative prior for all parameters. That is, we set :
- a_1 = a_2 = a_3 = 1,
- m_0 = (0, 0)^\top, C_0 = 10 \times I_2, and
- n_0 = d_0 = 1.
They are specified using the following code.
library(MCMCpack)Loading required package: codaLoading required package: MASS##
## Markov Chain Monte Carlo Package (MCMCpack)## Copyright (C) 2003-2025 Andrew D. Martin, Kevin M. Quinn, and Jong Hee Park##
## Support provided by the U.S. National Science Foundation## (Grants SES-0350646 and SES-0350613)
##library(mvtnorm)
##
p=2 ## order of AR process
K=3 ## number of mixing component
Y=matrix(y[3:200],ncol=1) ## y_{p+1:T}
Fmtx=matrix(c(y[2:199],y[1:198]),nrow=2,byrow=TRUE) ## design matrix F
n=length(Y) ## T-p
## prior hyperparameters
m0=matrix(rep(0,p),ncol=1)
C0=10*diag(p)
C0.inv=0.1*diag(p)
n0=1
d0=1
a=rep(1,K)112.0.4 Sampling Functions
sample_omega=function(L.cur){
n.vec=sapply(1:K, function(k){sum(L.cur==k)})
rdirichlet(1,a+n.vec)
}
sample_L_one=function(beta.cur,omega.cur,nu.cur,y.cur,Fmtx.cur){
prob_k=function(k){
beta.use=beta.cur[((k-1)*p+1):(k*p)]
omega.cur[k]*dnorm(y.cur,mean=sum(beta.use*Fmtx.cur),sd=sqrt(nu.cur[k]))
}
prob.vec=sapply(1:K, prob_k)
L.sample=sample(1:K,1,prob=prob.vec/sum(prob.vec))
return(L.sample)
}
sample_L=function(y,x,beta.cur,omega.cur,nu.cur){
L.new=sapply(1:n, function(j){sample_L_one(beta.cur,omega.cur,nu.cur,y.cur=y[j,],Fmtx.cur=x[,j])})
return(L.new)
}
sample_nu=function(k,L.cur){
idx.select=(L.cur==k)
n.k=sum(idx.select)
if(n.k==0){
d.k.star=d0
n.k.star=n0
}else{
y.tilde.k=Y[idx.select,]
Fmtx.tilde.k=Fmtx[,idx.select]
e.k=y.tilde.k-t(Fmtx.tilde.k)%*%m0
Q.k=t(Fmtx.tilde.k)%*%C0%*%Fmtx.tilde.k+diag(n.k)
Q.k.inv=chol2inv(chol(Q.k))
d.k.star=d0+t(e.k)%*%Q.k.inv%*%e.k
n.k.star=n0+n.k
}
1/rgamma(1,shape=n.k.star/2,rate=d.k.star/2)
}
sample_beta=function(k,L.cur,nu.cur){
nu.use=nu.cur[k]
idx.select=(L.cur==k)
n.k=sum(idx.select)
if(n.k==0){
m.k=m0
C.k=C0
}else{
y.tilde.k=Y[idx.select,]
Fmtx.tilde.k=Fmtx[,idx.select]
e.k=y.tilde.k-t(Fmtx.tilde.k)%*%m0
Q.k=t(Fmtx.tilde.k)%*%C0%*%Fmtx.tilde.k+diag(n.k)
Q.k.inv=chol2inv(chol(Q.k))
A.k=C0%*%Fmtx.tilde.k%*%Q.k.inv
m.k=m0+A.k%*%e.k
C.k=C0-A.k%*%Q.k%*%t(A.k)
}
rmvnorm(1,m.k,nu.use*C.k)
}112.0.5 The Gibbs Sampler
## number of iterations
nsim=20000
## store parameters
beta.mtx=matrix(0,nrow=p*K,ncol=nsim)
L.mtx=matrix(0,nrow=n,ncol=nsim)
omega.mtx=matrix(0,nrow=K,ncol=nsim)
nu.mtx=matrix(0,nrow=K,ncol=nsim)
## initial value
beta.cur=rep(0,p*K)
L.cur=rep(1,n)
omega.cur=rep(1/K,K)
nu.cur=rep(1,K)Now everything has been set up, we can start to code the loop.
Note it may take a while to complete the loop.
## Gibbs Sampler
for (i in 1:nsim) {
set.seed(i)
## sample omega
omega.cur=sample_omega(L.cur)
omega.mtx[,i]=omega.cur
## sample L
L.cur=sample_L(Y,Fmtx,beta.cur,omega.cur,nu.cur)
L.mtx[,i]=L.cur
## sample nu
nu.cur=sapply(1:K,function(k){sample_nu(k,L.cur)})
nu.mtx[,i]=nu.cur
## sample beta
beta.cur=as.vector(sapply(1:K, function(k){sample_beta(k,L.cur,nu.cur)}))
beta.mtx[,i]=beta.cur
## show the numer of iterations
if(i%%1000==0){
print(paste("Number of iterations:",i))
}
}[1] "Number of iterations: 1000"
[1] "Number of iterations: 2000"
[1] "Number of iterations: 3000"
[1] "Number of iterations: 4000"
[1] "Number of iterations: 5000"
[1] "Number of iterations: 6000"
[1] "Number of iterations: 7000"
[1] "Number of iterations: 8000"
[1] "Number of iterations: 9000"
[1] "Number of iterations: 10000"
[1] "Number of iterations: 11000"
[1] "Number of iterations: 12000"
[1] "Number of iterations: 13000"
[1] "Number of iterations: 14000"
[1] "Number of iterations: 15000"
[1] "Number of iterations: 16000"
[1] "Number of iterations: 17000"
[1] "Number of iterations: 18000"
[1] "Number of iterations: 19000"
[1] "Number of iterations: 20000"112.0.6 Checking the Posterior Inference Result
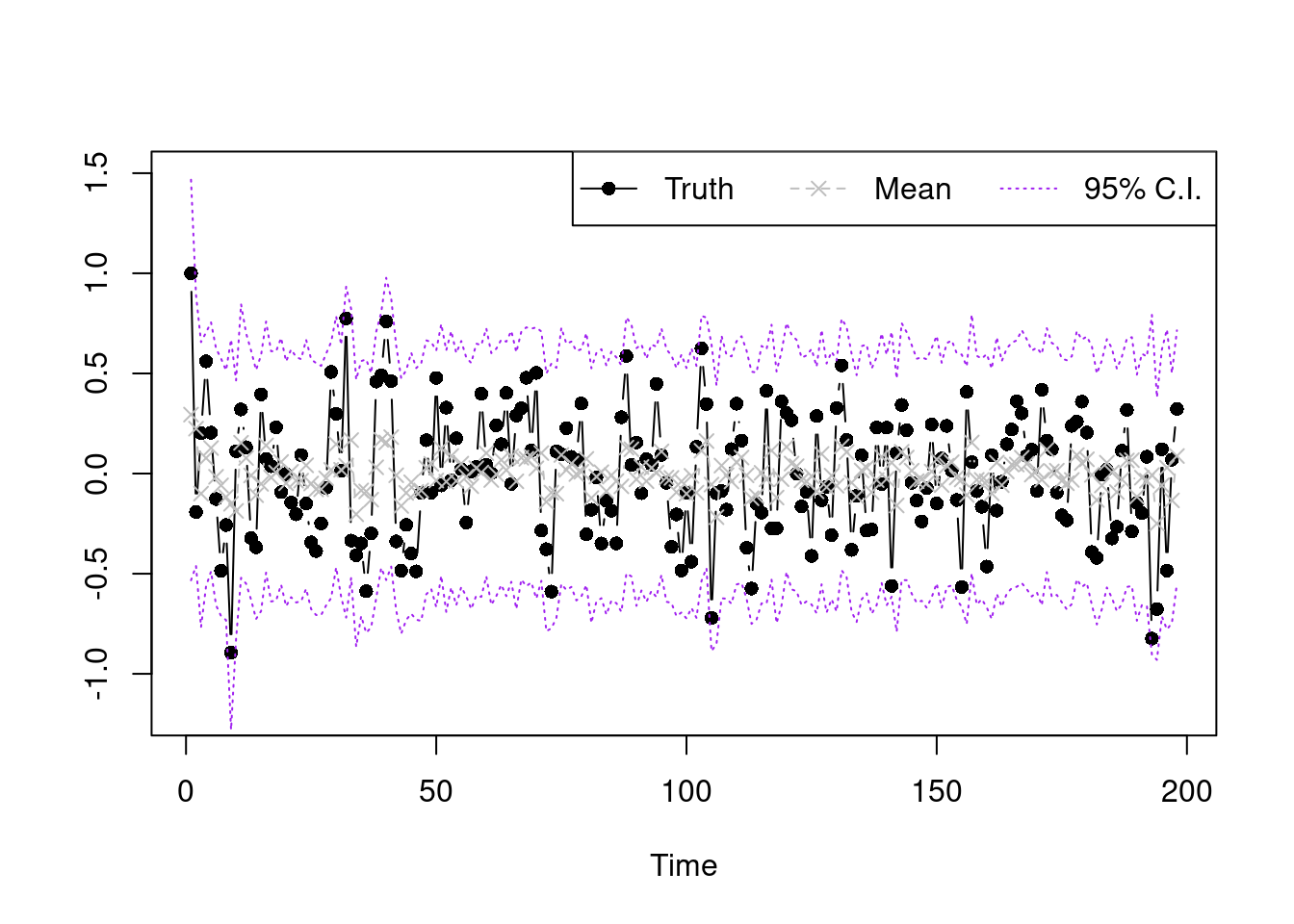
Finally, we plot the posterior mean and interval estimate of the original data using the later 10000 posterior samples, which is shown below.
sample.select.idx=seq(10001,20000,by=1)
post.pred.y.mix=function(idx){
k.vec.use=L.mtx[,idx]
beta.use=beta.mtx[,idx]
nu.use=nu.mtx[,idx]
get.mean=function(s){
k.use=k.vec.use[s]
sum(Fmtx[,s]*beta.use[((k.use-1)*p+1):(k.use*p)])
}
get.sd=function(s){
k.use=k.vec.use[s]
sqrt(nu.use[k.use])
}
mu.y=sapply(1:n, get.mean)
sd.y=sapply(1:n, get.sd)
sapply(1:length(mu.y), function(k){rnorm(1,mu.y[k],sd.y[k])})
}
y.post.pred.sample=sapply(sample.select.idx, post.pred.y.mix)
summary.vec95=function(vec){
c(unname(quantile(vec,0.025)),mean(vec),unname(quantile(vec,0.975)))
}
summary.y=apply(y.post.pred.sample,MARGIN=1,summary.vec95)
plot(Y,type='b',xlab='Time',ylab='',pch=16,ylim=c(-1.2,1.5))
lines(summary.y[2,],type='b',col='grey',lty=2,pch=4)
lines(summary.y[1,],type='l',col='purple',lty=3)
lines(summary.y[3,],type='l',col='purple',lty=3)
legend("topright",legend=c('Truth','Mean','95% C.I.'),lty=1:3,
col=c('black','grey','purple'),horiz = T,pch=c(16,4,NA))