Time series analysis for coupled neurons.

pydata global

TipLecture Overview

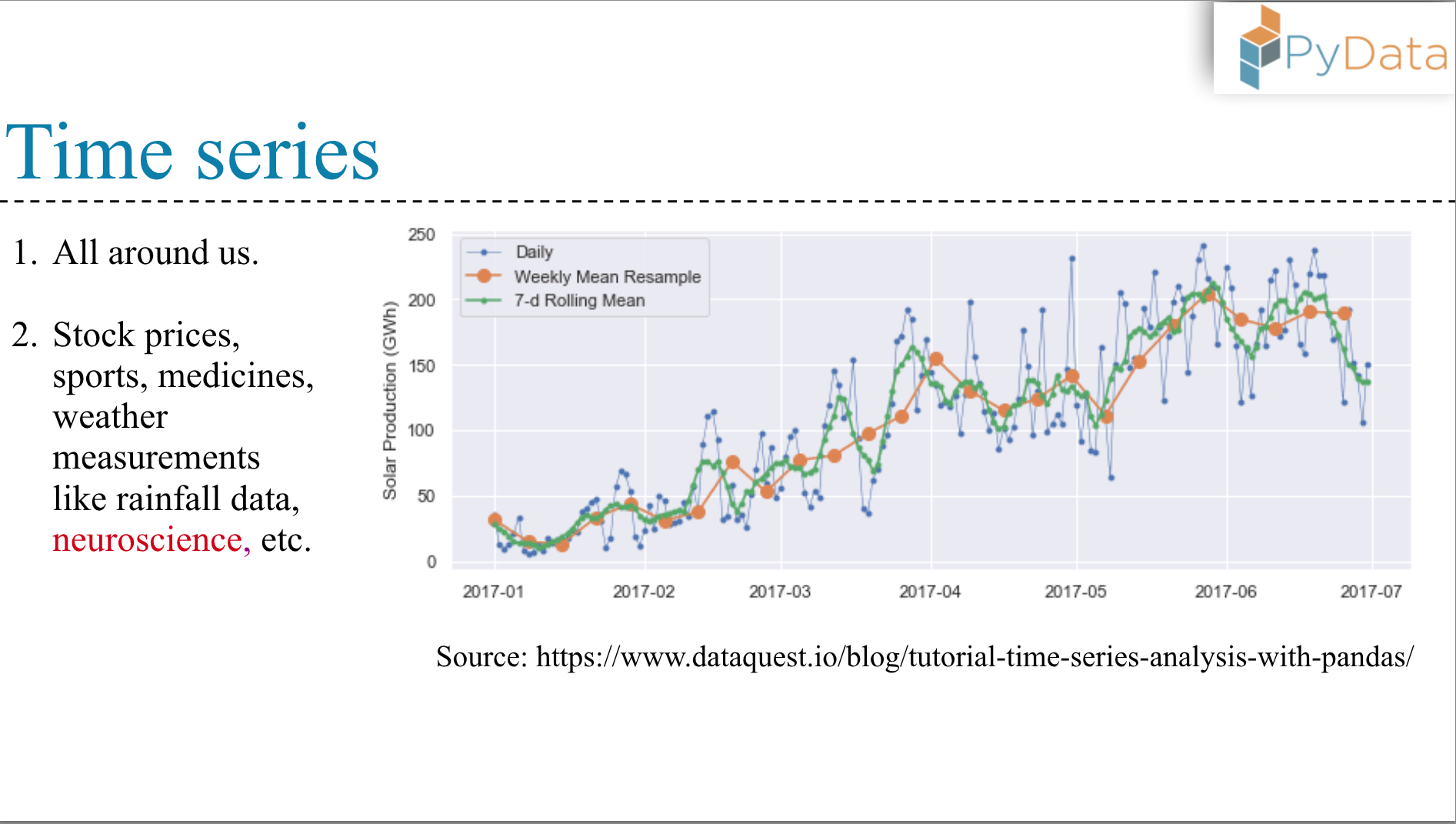
The complex nervous system provides a repertoire of evolutionary properties like neuron spiking, bursting, and chaos that are yet to be fully understood.

One approach is to tackle these time-dependent properties using the technique of “dynamical systems”, such as ordinary differential equations. Since the popular work by Hodgkin and Huxley, many dynamical systems models of neurons have been proposed, of which FitzHugh–Nagumo and Morris–Lecar models draw special attention.

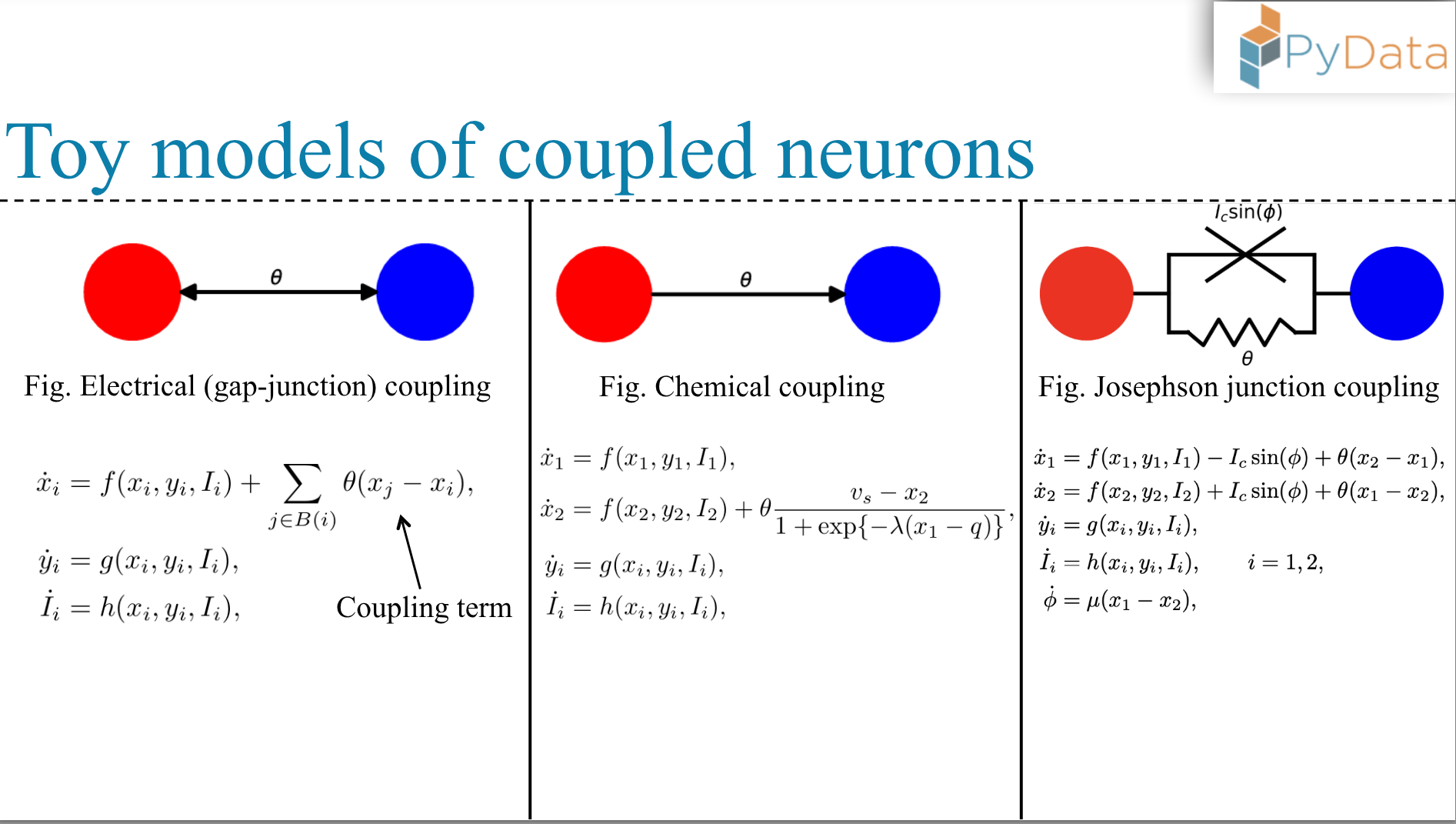
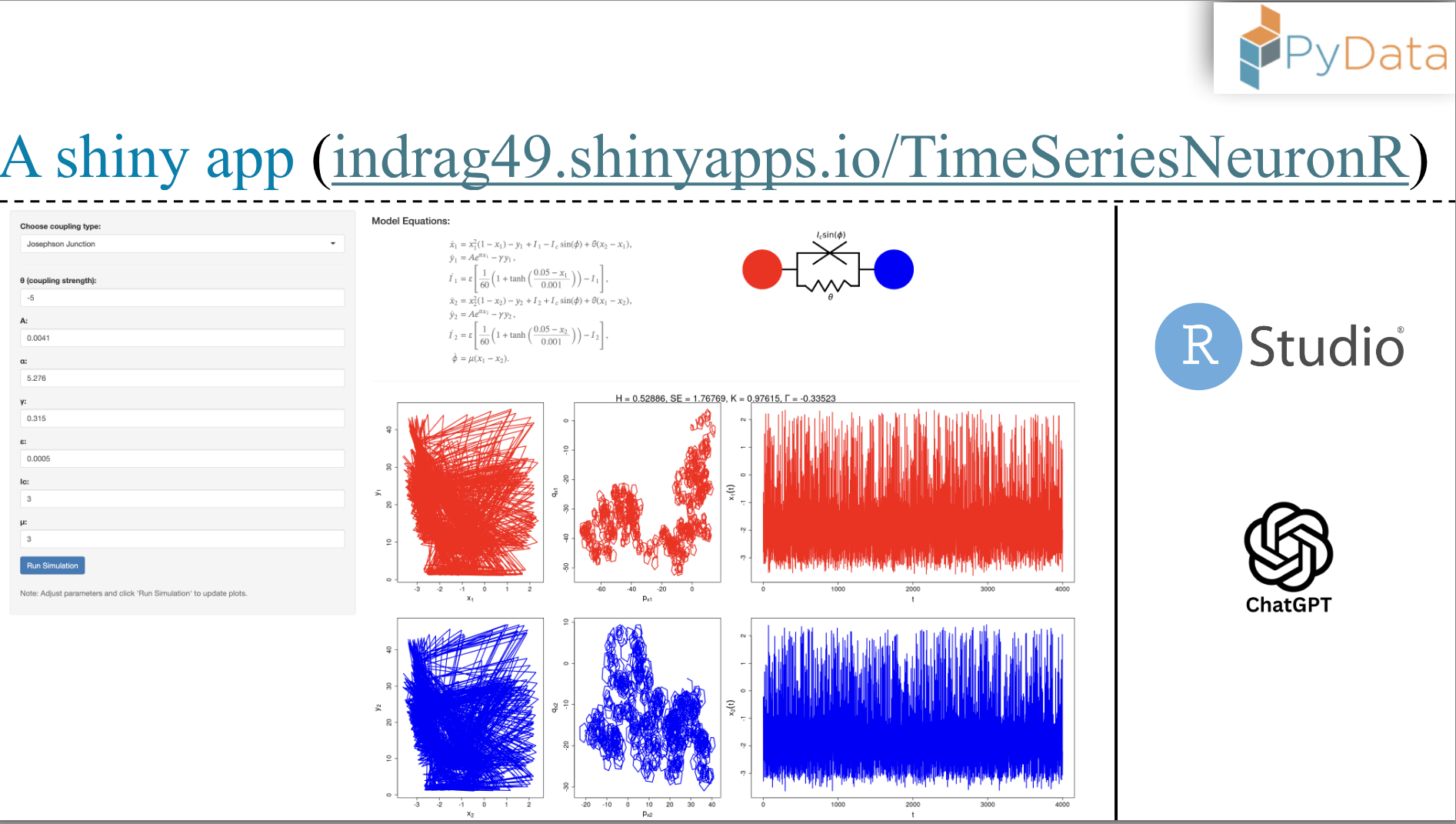
The nervous system is made of a network of neurons, possessing a complex structural and functional topology. This topology is a function of different parameters, among which the coupling strength plays a major role. Our focus would be to systematically study the effect of various coupling strategies on the firing patterns exhibited by a collection of neurons.

In this workshop, my goal is to popularize a reduced-order model of neuron dynamics known as the “denatured Morris–Lecar” system and to teach how Python can be efficiently used to perform research on time series analysis of coupled neurons.

This is a tutorial on hands-on time series analysis of coupled neuron models. We will build mathematical models of coupled neurons, and then utilize tools from nonlinear dynamics to analyze simulated time series. We will discuss various empirically informed coupling strategies and statistically efficient time series measures. This workshop is 100% Jupyter notebook and will have room to openly brainstorm ideas to extend and improve the studies. Let’s unravel some complex dynamics together!

The pipeline of this tutorial will be the following:

1. Start by building a coupled neuron system based on different coupling strategies,
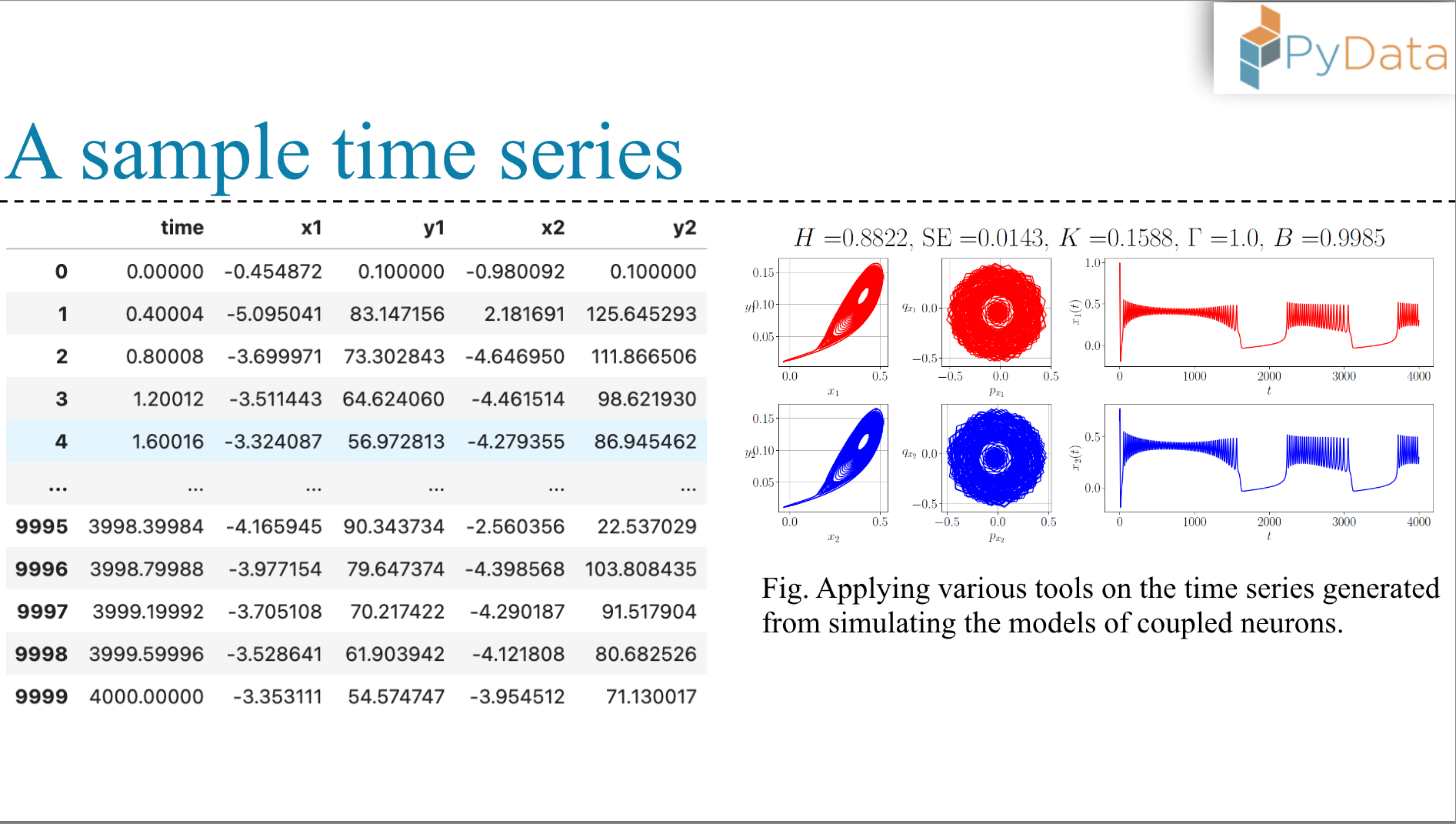
2. Simulate the system and generate time series data,
3. Perform time series analysis by computing various metrics from the nonlinear dynamics literature,
4. Finally, discuss what these metrics tell us about the temporal behavior of neurons.

Coupling strategies we are going to look at:

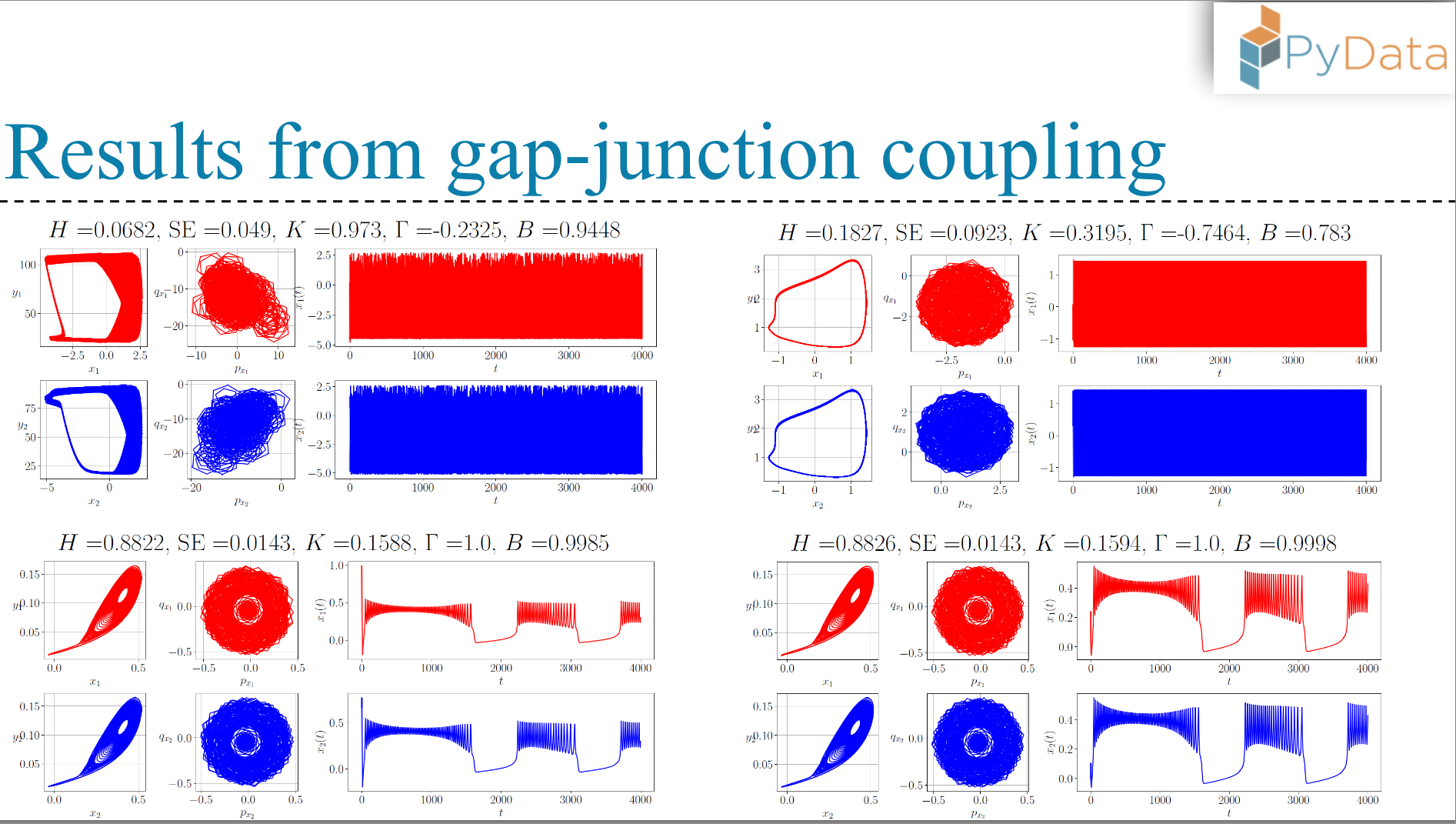
1. Gap junction coupling
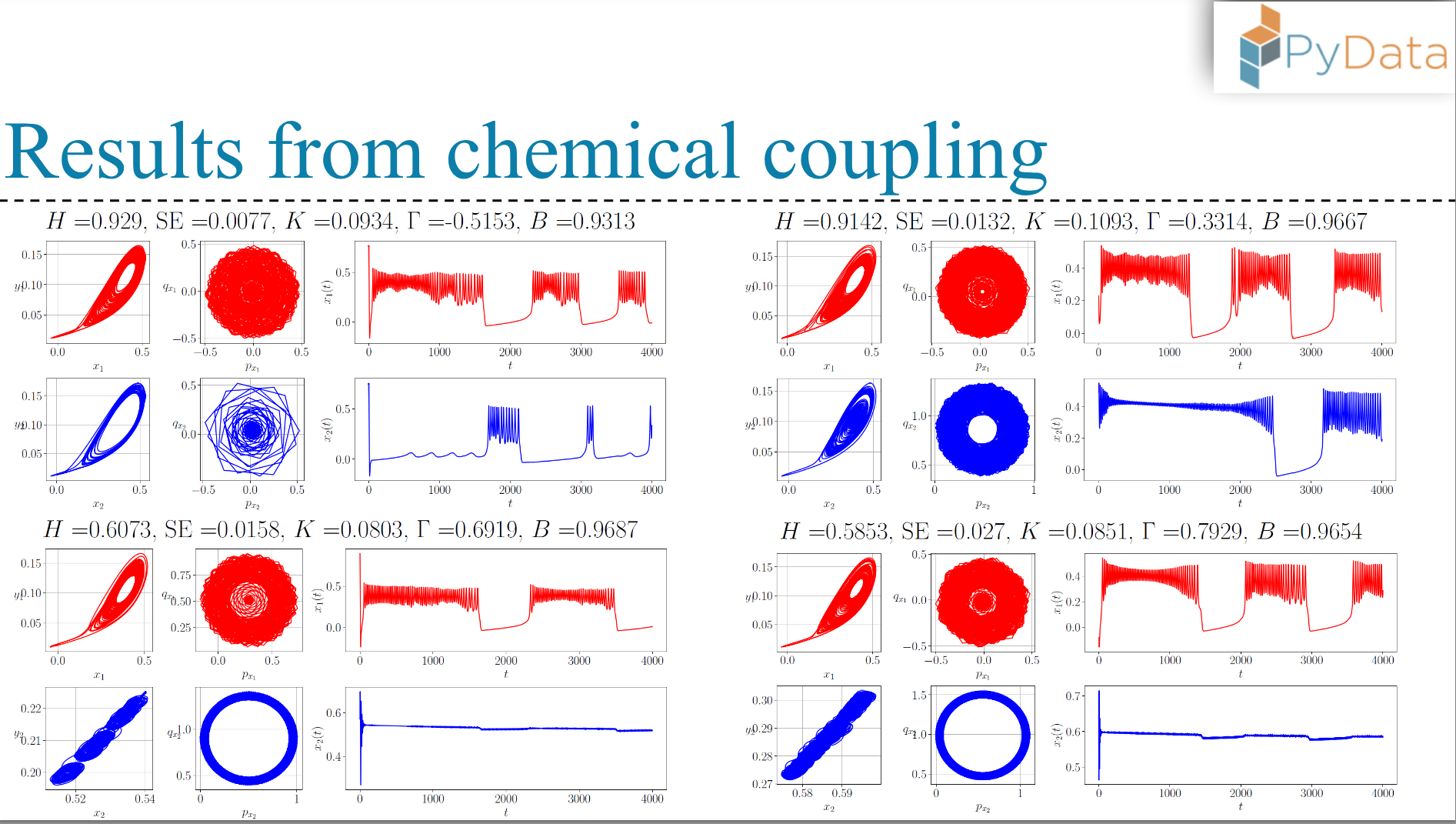
2. Chemical coupling
3. A hybrid coupling influenced by a superconductor model in physics
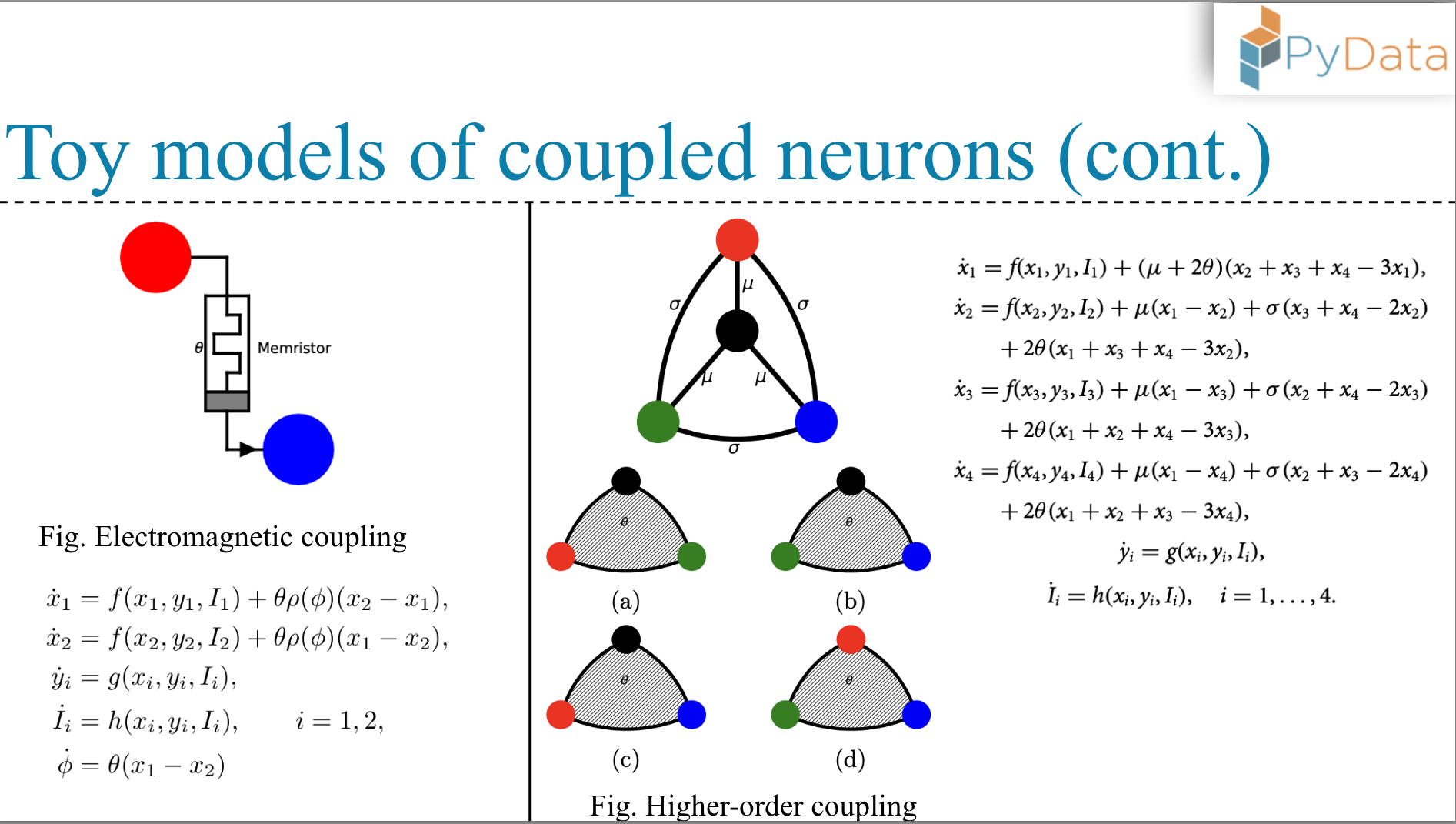
4. Electromagnetic coupling
5. Coupling, which is not pairwise but higher-order (A bit of background on graph theory is recommended)
6. A random coupling strategy

The audience would find this interesting because it would be a hands-on introduction to how the mechanisms of neurons can be explored using different tools from the nonlinear dynamics literature. Mathematically modelling the dynamics of neurons has attracted several researchers in recent years because of the popularity of artificial intelligence. This field of neuron dynamics is booming, and delivering this workshop would be timely. I would also ensure to leave some room for brainstorming further ideas with the audience and how this study could be potentially extended and improved, thus an interactive session.

The goal is to attract applied mathematicians, computer scientists, data scientists, engineers, and statisticians alike and provide them with a battery of tools to add to their knowledge base. The audience would then be able to apply these tools in domains other than neurodynamics, for example, climate, finance, or social science. The only technical background I would expect from the audience is familiarity with matplotlib, numpy and pandas, and some basic statistics (regression, correlation coefficient), linear algebra (matrix operations), and graphs (as in networks). After the tutorial, the audience will leave with a newly built insight into the mathematical modeling of neuron dynamics.

TipWhat You’ll Learn:

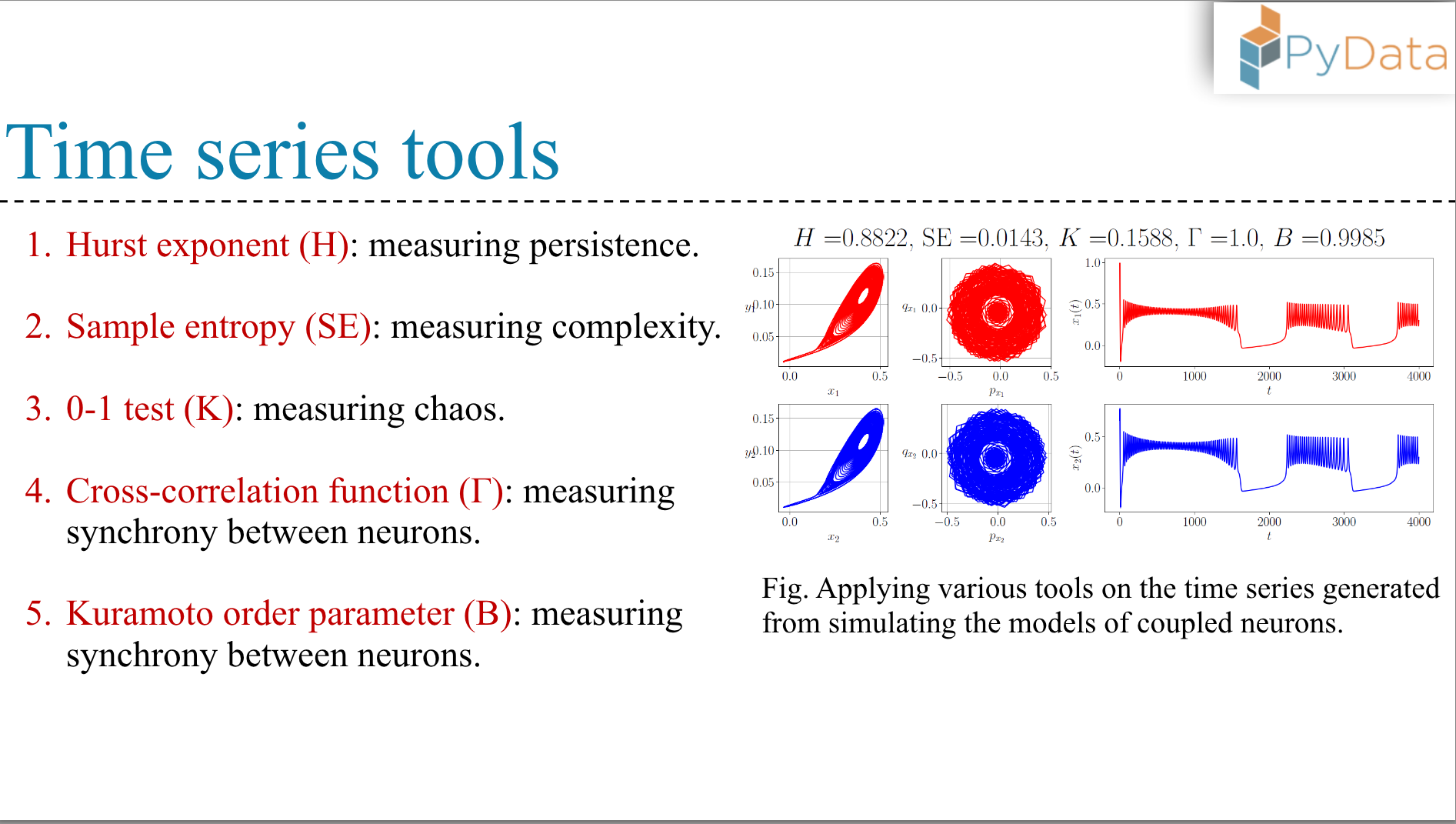
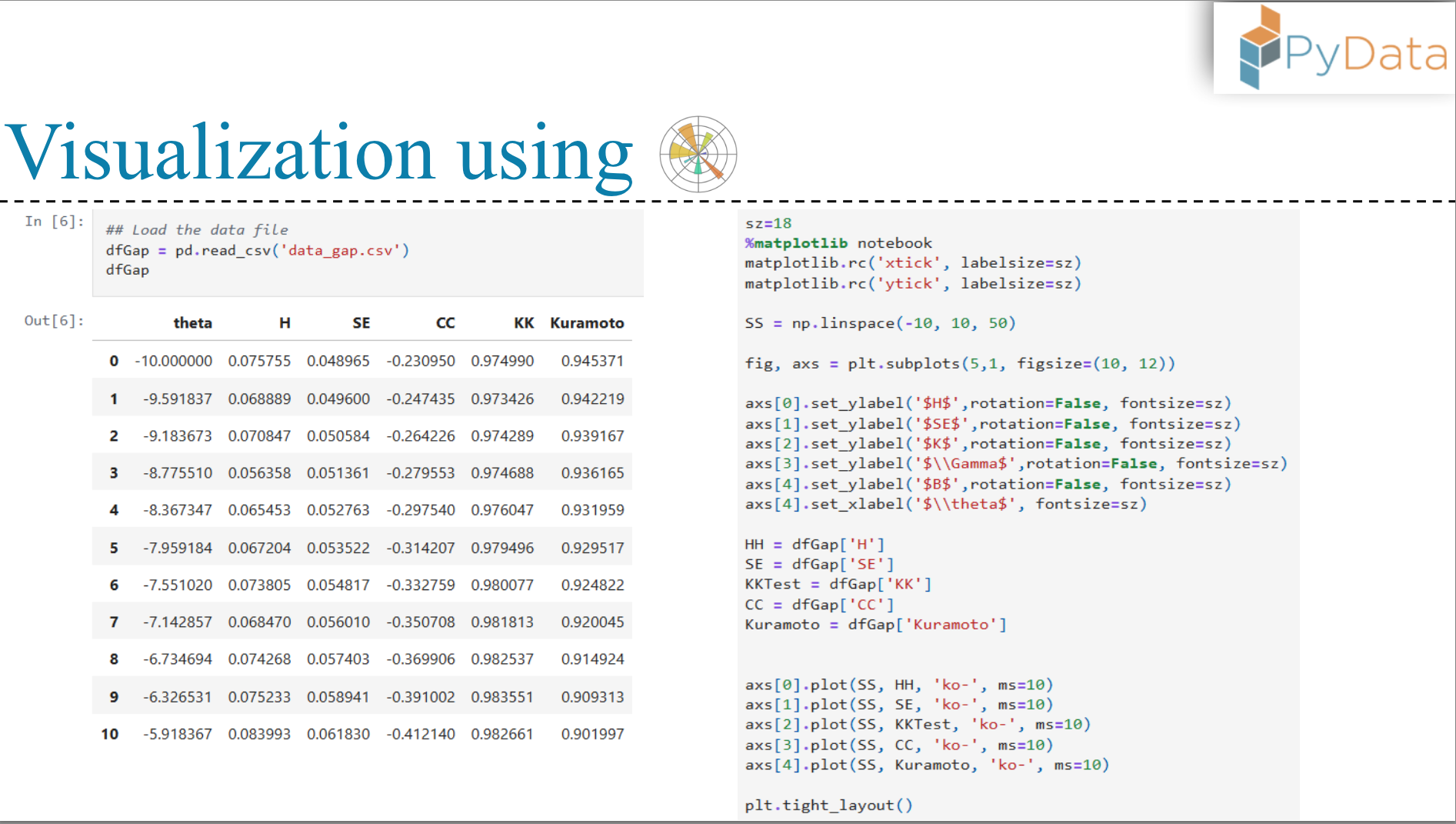
We will implement the following methodologies/algorithms for time series analysis of coupled neuron models:

1. Hurst exponent: measuring persistence of time series,
2. Sample entropy: measuring the complexity of time series,
3. 0–1 test: measuring chaos,
4. Kuramoto order-parameter: measuring synchrony between the neurons.

TipPrerequisites:

• Basic Python and PyTorch
• Some familiarity with neural networks (e.g., feedforward, softmax)
• No need for prior experience in building models from scratch

TipTools and Frameworks:

This tutorial is 100% Python. And I will be utilizing Jupyter Notebooks to deliver the workshop. Packages that need to be downloaded beforehand are:

1. matplotlib for plotting,
2. numpy and scipy for scientific computations,
3. nolds for nonlinear measure for dynamical systems,
4. pandas for data handling.

workshop repo

TipSpeakers:

Indranil Ghosh

Indra is a postdoctoral fellow in applied mathematics at Massey University, New Zealand, working on all things “dynamical systems”. He takes a computational approach to tackle complex problems, and his current research is focused on understanding collective behaviour exhibited by coupled neurons. He is an avid Python user and has been a speaker at multiple Python-related conferences before. More information can be found in his website: https://indrag49.github.io/.

Outline

0–15 mins: Introduction to neurons as dynamical systems and why we care about their behavior over time. We will talk about a single neuron’s behavior and the selection of a mathematical model. We will also talk about the bursting phenomenon in neurons.

15-30 mins: We will then mathematically model a coupled system of neurons. We will cover the topic of “small networks” of neurons and what they teach us about the bigger picture: a complex, connected nervous system.

30-45 mins: Next, we will introduce various empirically informed coupling mechanisms. We will talk about how these couplings incorporate different firing patterns in the coupled neurons, ranging from regular behavior to chaotic firing.

45-75 mins: Finally, I will introduce time series analysis of neuron data. We will then implement the algorithms mentioned above to realize different dynamical properties of the neurons.

75-90 mins: Open the room to QA and brainstorm further ideas to improve/extend the analysis of neuron-time series data.

TipHighlights

article - Taming the Chaos of Computational Experiments

main points:

1. Use Version Control (Preferably Git)
2. Separate Experiments From Figures
3. Create Human-digestible Logs
4. Log Details of Individual Runs
5. Use Scripts for Automation
6. Separate and Organize Your Project Components
7. Share Your Code, Data, and Experimental Logs

(listed in roughly increasing order of difficulty)

Reflection

This is a very exciting talk.

First of all it is the first time I see work on simulation of (coupled) neurons, a topic that get mentioned all too ofthen in popular science on chaos, dynamical systems, and complex systems, but rarely in practical terms.

I have taken a few courses on time series which might be relevant but this is both a new problem and a new set of tools for me.

Near the end of the talk we discuss networks of neurons, which is another topic altogether and it appears that there should be more exploration in this area - perhaps about criticality, percolation, and emergence.

The talk is well structured, with a clear outline and flow. The speaker clearly explains the motivation behind studying coupled neurons and the relevance of time series analysis in this context. The use of Python and Jupyter Notebooks makes the workshop accessible and practical.

---

Some ideas

1. using dlm as a black box to model neuron time series data
2. using a kalman filter to denoise neuron time series data or to predict future states based on laplace transform methods.
3. Are there control applications here?
   1. (can a neuron drive coupled neurons into excitatory or inhibitory states using optimal control methods?)
   2. can these neurons be used to as model for information themselves. Like a more realistic RNN model. This might lead to new insights about catastrophical forgetting and loss of plasticity in ANNs.
   3. can they work as a classifier, regressor, rl agent?
   4. in a network are there nodes that act as pain pleasure centers that can be targeted for RL rewards and punishments? This might suggest new architectures for modeling reinforcement learning agents - or at least a new way of implementing the reward/punishment mechanisms in say the OAK architecture recently described by Rich Sutton.
   5. In a node are there structually placed neurons we might destroy to prevent siezure regimes? A kind of electroshock therapy for epilepsy?
   
   
4. also the neurons might have several regimes (both individual and collectively) this suggest the use switching mixture markov models.
5. I would think a good challenge would be to build poincare maps of the neuron dynamics and use them to classify the different regimes of the neurons. This would then be useful to setup the switching markov model.
6. question: Can one add a new chaotic components to the already versatile DLM that is inspired by long term dependencies. It could include some form of fractional differencing or fractional integration.
7. can we convert the shiny app to a shinylive app so it runs just in the browser and does not need a server?
8. popular video You’ve (Likely) Been Playing The Game of Life Wrong

You’ve (Likely) Been Playing The Game of Life Wrong

TipTODO

• add citations to the various resources mentioned in the talk.
• embed the shiny app or at least link to it.
• link to the github repo with the notebooks.
• quick review Taming the Chaos of Computational Experiments