---
date: 2024-01-10
title: SuperLearner
description: SuperLearner is an ensambeleing library.
categories: [demos,code,r]
engine: knitr
format:
html:
code-fold: False
code-tools: True
code-link: True
df-print: kable
execute:
cache: True
capture: True
freeze: auto # re-render only when source changes
---
This is a SuperLearner demo.
SuperLearner is an ensambeleing library.
This page is taken out of the documentation
## Setup dataset
```{r}
#| label: lst-mass-data-set
#| lst-label: lst-mass-data-set
#| lst-cap: dataset setup
#install.packages(c("SuperLearner","caret", "glmnet", "randomForest", "ggplot2", "RhpcBLASctl","xgboost","ranger"))
data(Boston, package = "MASS")
?MASS::Boston # Review info on the Boston dataset.>
colSums(is.na(Boston)) # Check for any missing data - looks like we don't have any.
outcome = Boston$medv #Extract our outcome variable from the dataframe.
data = subset(Boston, select = -medv) # Create a dataframe to contain our explanatory variables.
head(data)
str(data) # Check structure of our dataframe.
dim(data) # Review our dimensions.
set.seed(1)# Set a seed for reproducibility in this random sampling.
train_obs = sample(nrow(data), 150) # Reduce to a dataset of 150 observations to speed up model fitting.
x_train = data[train_obs, ] # X is our training sample.
x_holdout = data[-train_obs, ] # Create a holdout set for evaluating model performance.
# Note: cross-validation is even better than a single holdout sample.
outcome_bin = as.numeric(outcome > 22) # Create a binary outcome variable: towns in which median home value is > 22,000.
y_train = outcome_bin[train_obs]
y_holdout = outcome_bin[-train_obs]
table(y_train, useNA = "ifany") # Review the outcome variable distribution.
```
## Review available models
```{r}
#| label: lst-model-review
#| lst-label: lst-model-review
#| lst-cap: model review
library(SuperLearner)
listWrappers() # Review available models.
SL.glmnet
```
## Fit individual models
Let’s fit 2 separate models: lasso (sparse, penalized OLS) and random forest. We specify family = binomial() because we are predicting a binary outcome, aka classification. With a continuous outcome we would specify family = gaussian().
```{r}
#| label: lst-model-fit-lasso
#| lst-label: lst-model-fit-lasso
#| lst-cap: fit lasso
set.seed(1) # Set the seed for reproducibility.
sl_lasso = SuperLearner(Y = y_train, X = x_train, family = binomial(),
SL.library = "SL.glmnet") # Fit lasso model.
sl_lasso
names(sl_lasso)
sl_lasso$cvRisk[which.min(sl_lasso$cvRisk)]
str(sl_lasso$fitLibrary$SL.glmnet_All$object, max.level = 1)
sl_rf = SuperLearner(Y = y_train, X = x_train, family = binomial(),
SL.library = "SL.ranger")
names(sl_lasso)
sl_lasso$cvRisk[which.min(sl_lasso$cvRisk)]
# Here is the raw glmnet result object:
str(sl_lasso$fitLibrary$SL.glmnet_All$object, max.level = 1)
```
```{r}
# Fit random forest.
sl_rf = SuperLearner(Y = y_train, X = x_train, family = binomial(), SL.library = "SL.ranger")
sl_rf
```
## Fit multiple models
```{r}
#| label: lst-fit-multiple-models
#| lst-label: lst-fit-multiple-models
#| lst-cap: lst fit multiple models
set.seed(1)
sl = SuperLearner(Y = y_train, X = x_train, family = binomial(),
SL.library = c("SL.mean", "SL.glmnet", "SL.ranger"))
sl
sl$times$everything
```
Again, the coefficient is how much weight SuperLearner puts on that model in the weighted-average. So if coefficient = 0 it means that model is not used at all. Here we see that random forest is given the most weight, following by lasso.
So we have an automatic ensemble of multiple learners based on the cross-validated performance of those learners, nice!
# Predict on new data
Now that we have an ensemble let’s predict back on our holdout dataset and review the results.
```{r}
#| label: lst-predict
#| lst-label: lst-predict
#| lst-cap: predict
#| # Predict back on the holdout dataset.
# onlySL is set to TRUE so we don't fit algorithms that had weight = 0, saving computation.
pred = predict(sl, x_holdout, onlySL = TRUE)
# Check the structure of this prediction object.
str(pred)
# Review the columns of $library.predict.
summary(pred$library.predict)
library(ggplot2)
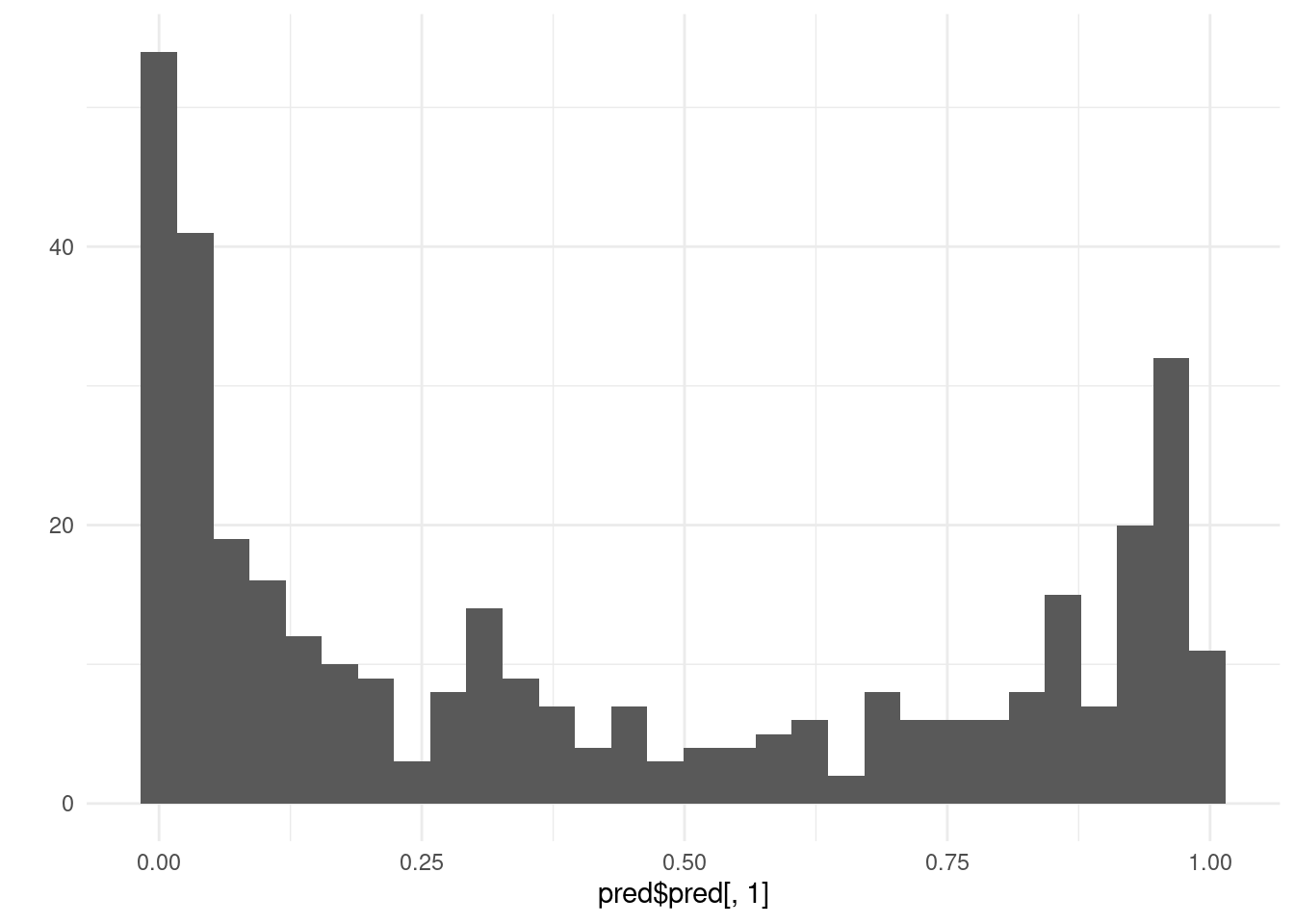
qplot(pred$pred[, 1]) + theme_minimal()
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
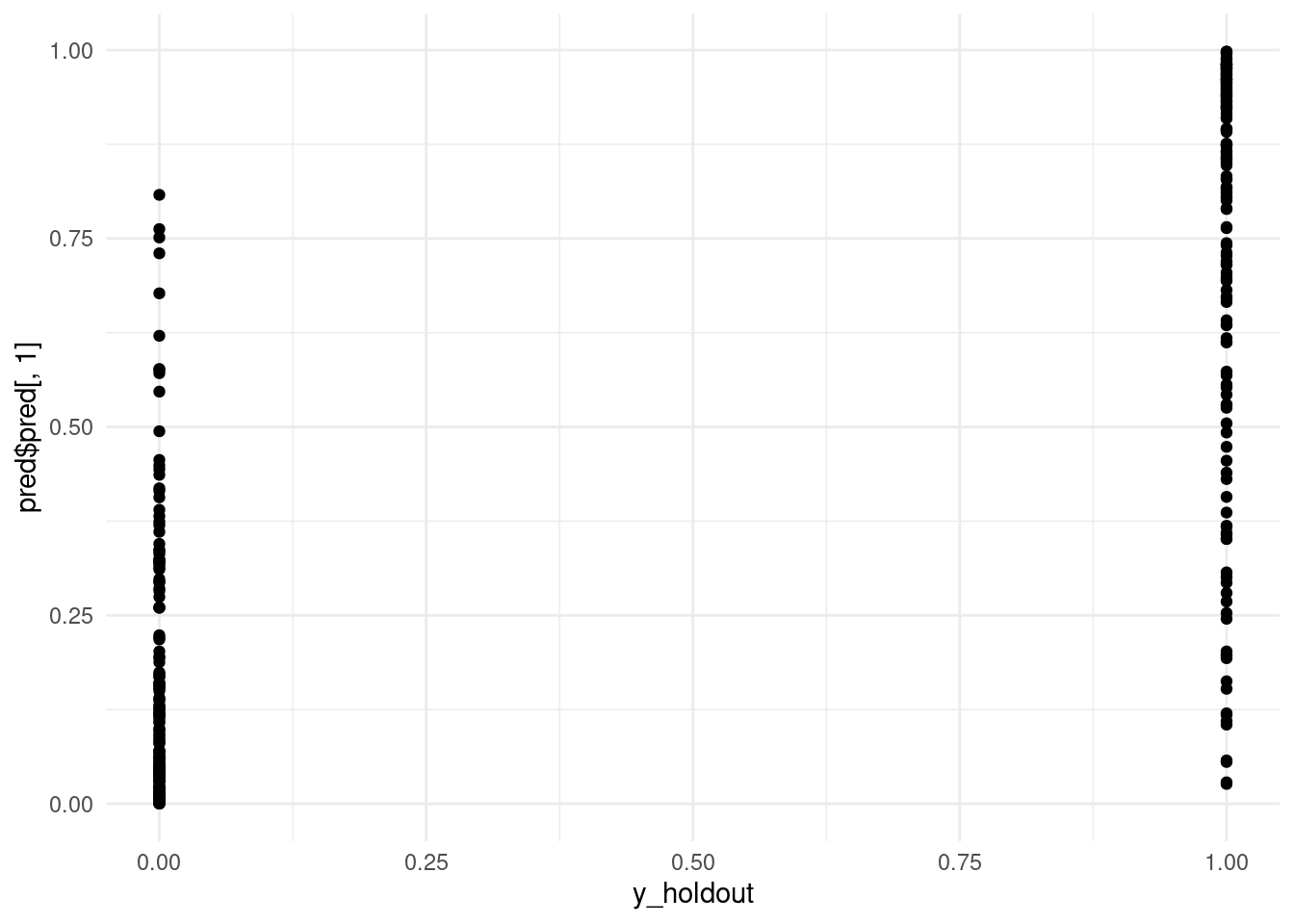
# Scatterplot of original values (0, 1) and predicted values.
# Ideally we would use jitter or slight transparency to deal with overlap.
qplot(y_holdout, pred$pred[, 1]) + theme_minimal()
# Review AUC - Area Under Curve
pred_rocr = ROCR::prediction(pred$pred, y_holdout)
auc = ROCR::performance(pred_rocr, measure = "auc", x.measure = "cutoff")@y.values[[1]]
auc
```
# Fit ensemble with external cross-validation
What we don’t have yet is an estimate of the performance of the ensemble itself. Right now we are just hopeful that the ensemble weights are successful in improving over the best single algorithm.
In order to estimate the performance of the SuperLearner ensemble we need an “external” layer of cross-validation, also called **nested cross-validation**. We generate a separate holdout sample that we don’t use to fit the SuperLearner, which allows it to be a good estimate of the SuperLearner’s performance on unseen data. Typically we would run 10 or 20-fold external cross-validation, but even 5-fold is reasonable.
Another nice result is that we get standard errors on the performance of the individual algorithms and can compare them to the SuperLearner.
```{r}
set.seed(1)
# Don't have timing info for the CV.SuperLearner unfortunately.
# So we need to time it manually.
system.time({
# This will take about 2x as long as the previous SuperLearner.
cv_sl = CV.SuperLearner(Y = y_train, X = x_train, family = binomial(),
# For a real analysis we would use V = 10.
V = 3,
SL.library = c("SL.mean", "SL.glmnet", "SL.ranger"))
})
# We run summary on the cv_sl object rather than simply printing the object.
summary(cv_sl)
# Review the distribution of the best single learner as external CV folds.
table(simplify2array(cv_sl$whichDiscreteSL))
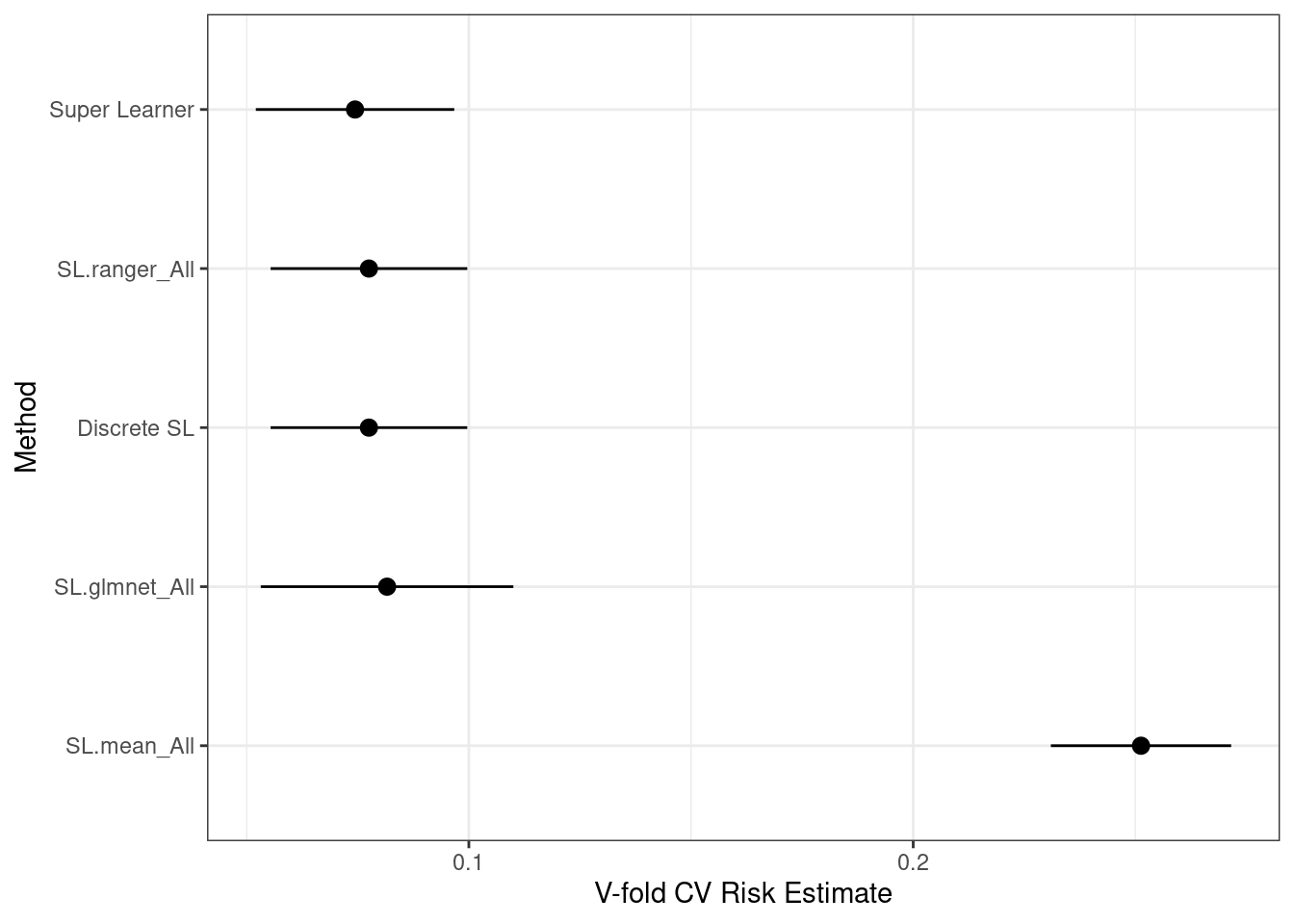
# Plot the performance with 95% CIs (use a better ggplot theme).
plot(cv_sl) + theme_bw()
ggsave("SuperLearner.png")
```
## Customize a model hyperparameter
Hyperparameters are the configuration settings for an algorithm. OLS has no hyperparameters but essentially every other algorithm does.
There are two ways to customize a hyperparameter: make a new learner function, or use create.Learner().
Let’s make a variant of random forest that fits more trees, which may increase our accuracy and can’t hurt it (outside of small random variation).
```{r}
# Review the function argument defaults at the top.
SL.ranger
# Create a new function that changes just the ntree argument.
# (We could do this in a single line.)
# "..." means "all other arguments that were sent to the function"
SL.rf.better = function(...) {
SL.randomForest(..., num.trees = 1000)
}
set.seed(1)
# Fit the CV.SuperLearner.
# We use V = 3 to save computation time; for a real analysis use V = 10 or 20.
cv_sl = CV.SuperLearner(Y = y_train, X = x_train, family = binomial(), V = 3,
SL.library = c("SL.mean", "SL.glmnet", "SL.rf.better", "SL.ranger"))
# Review results.
summary(cv_sl)
# Customize the defaults for random forest.
learners = create.Learner("SL.ranger", params = list(num.trees = 1000))
# Look at the object.
learners
# List the functions that were created
learners$names
# Review the code that was automatically generated for the function.
# Notice that it's exactly the same as the function we made manually.
SL.ranger_1
set.seed(1)
# Fit the CV.SuperLearner.
# We use V = 3 to save computation time; for a real analysis use V = 10 or 20.
cv_sl = CV.SuperLearner(Y = y_train, X = x_train, family = binomial(),
V = 3,
SL.library = c("SL.mean", "SL.glmnet", learners$names, "SL.ranger"))
# Review results.
summary(cv_sl)
```
## Test algorithm with multiple hyperparameter settings
The performance of an algorithm varies based on its hyperparamters, which again are its configuration settings. Some algorithms may not vary much, and others might have far better or worse performance for certain settings. Often we focus our attention on 1 or 2 hyperparameters for a given algorithm because they are the most important ones.
For random forest there are two particularly important hyperparameters: mtry and maximum leaf nodes. Mtry is how many features are randomly chosen within each decision tree node - in other words, each time the tree considers making a split. Maximum leaf nodes controls how complex each tree can get.
Let’s try 3 different mtry options.
```{r}
# sqrt(p) is the default value of mtry for classification.
floor(sqrt(ncol(x_train)))
## [1] 3
# Let's try 3 multiplies of this default: 0.5, 1, and 2.
(mtry_seq = floor(sqrt(ncol(x_train)) * c(0.5, 1, 2)))
## [1] 1 3 7
learners = create.Learner("SL.ranger", tune = list(mtry = mtry_seq))
# Review the resulting object
learners
SL.ranger_1
SL.ranger_2
SL.ranger_3
set.seed(1)
# Fit the CV.SuperLearner.
# We use V = 3 to save computation time; for a real analysis use V = 10 or 20.
cv_sl = CV.SuperLearner(Y = y_train, X = x_train,
family = binomial(), V = 3,
SL.library = c("SL.mean", "SL.glmnet", learners$names, "SL.ranger"))
# Review results.
summary(cv_sl)
```
We see here that mtry = 7 performed a little bit better than mtry = 1 or mtry = 3, although the difference is not significant. If we used more data and more cross-validation folds we might see more drastic differences. A higher mtry does better when a small percentage of variables are predictive of the outcome, because it gives each tree a better chance of finding a useful variable.
Note that SL.ranger and SL.ranger_2 have the same settings, and their performance is very similar - statistically a tie. It’s not exactly equivalent due to random variation in the two forests.
A key difference with SuperLearner over caret or other frameworks is that we are not trying to choose the single best hyperparameter or model. Instead, we usually want the best weighted average. So we are including all of the different settings in our SuperLearner, and we may choose a weighted average that includes the same model multiple times but with different settings. That can give us better performance than choosing only the single best settings for a given algorithm, which has some random noise in any case.
Multicore parallelization
SuperLearner makes it easy to use multiple CPU cores on your computer to speed up the calculations. We first need to setup R for multiple cores, then tell CV.SuperLearner to divide its computations across those cores.
There are two ways to use multiple cores in R: the “multicore” system and the “snow” system. Windows only supports the “snow” system, which is more difficult to use, whereas macOS and Linux can use either one.
First we show the “multicore” system version:
```{r}
# Setup parallel computation - use all cores on our computer.
(num_cores = RhpcBLASctl::get_num_cores())
# Use 2 of those cores for parallel SuperLearner.
# Replace "2" with "num_cores" (without quotes) to use all cores.
options(mc.cores = 2)
# Check how many parallel workers we are using (on macOS/Linux).
getOption("mc.cores")
# We need to set a different type of seed that works across cores.
# Otherwise the other cores will go rogue and we won't get repeatable results.
# This version is for the "multicore" parallel system in R.
set.seed(1, "L'Ecuyer-CMRG")
# While this is running check CPU using in Activity Monitor / Task Manager.
system.time({
cv_sl = CV.SuperLearner(Y = y_train, X = x_train, family = binomial(),
# For a real analysis we would use V = 10.
V = 3,
parallel = "multicore",
SL.library = c("SL.mean", "SL.glmnet", learners$names, "SL.ranger"))
})
# Review results.
summary(cv_sl)
```
Here is the “snow” equivalent:
```{r}
# Make a snow cluster
# Again, replace 2 with num_cores to use all available cores.
cluster = parallel::makeCluster(2)
# Check the cluster object.
cluster
# Load the SuperLearner package on all workers so they can find
# SuperLearner::All(), the default screening function which keeps all variables.
parallel::clusterEvalQ(cluster, library(SuperLearner))
# We need to explictly export our custom learner functions to the workers.
parallel::clusterExport(cluster, learners$names)
# We need to set a different type of seed that works across cores.
# This version is for SNOW parallelization.
# Otherwise the other cores will go rogue and we won't get repeatable results.
parallel::clusterSetRNGStream(cluster, 1)
# While this is running check CPU using in Activity Monitor / Task Manager.
system.time({
cv_sl = CV.SuperLearner(Y = y_train, X = x_train, family = binomial(),
# For a real analysis we would use V = 10.
V = 3,
parallel = cluster,
SL.library = c("SL.mean", "SL.glmnet", learners$names, "SL.ranger"))
})
# Review results.
summary(cv_sl)
# Stop the cluster workers now that we're done.
parallel::stopCluster(cluster)
```
If we want to use multiple cores for normal SuperLearner, not CV.SuperLearner (i.e. external cross-validation to estimate performance), we need to change the function name to mcSuperLearner (“multicore” version) or snowSuperLearner (“snow” version).
First the “multicore” version (won’t be parallel on Windows):
```{r}
# Set multicore compatible seed.
set.seed(1, "L'Ecuyer-CMRG")
# Fit the SuperLearner.
(sl = mcSuperLearner(Y = y_train, X = x_train, family = binomial(),
SL.library = c("SL.mean", "SL.glmnet", learners$names, "SL.ranger")))
# We see the time is reduced over our initial single-core superlearner.
sl$times$everything
```
Now the “snow” version, which should be parallel on all operating systems.
```{r}
# Make a snow cluster
# Reminder: change "2" to "num_cores" (without quotes) to use all available cores.
(cluster = parallel::makeCluster(2))
## socket cluster with 2 nodes on host 'localhost'
# Load the SuperLearner package on all workers so they can find
# SuperLearner::All(), the default screening function which keeps all variables.
parallel::clusterEvalQ(cluster, library(SuperLearner))
# We need to explictly export our custom learner functions to the workers.
parallel::clusterExport(cluster, learners$names)
# We need to set a different type of seed that works across cores.
# This version is for SNOW parallelization.
# Otherwise the other cores will go rogue and we won't get repeatable results.
parallel::clusterSetRNGStream(cluster, 1)
# Fit the SuperLearner.
(sl = snowSuperLearner(Y = y_train, X = x_train, family = binomial(),
cluster = cluster,
SL.library = c("SL.mean", "SL.glmnet", learners$names, "SL.ranger")))
# We see the time is reduced over our initial single-core superlearner.
sl$times$everything
```
SuperLearner also supports running across multiple computers at a time, called “multi-node” or “cluster” computing. We will skip that for now.
## Weight distribution for SuperLearner
The weights or coefficients of the SuperLearner are stochastic - they will change as the data changes. So we don’t necessarily trust a given set of weights as being the “true” weights, but when we use CV.SuperLearner we at least have multiple samples from the distribution of the weights.
We can write a little function to extract the weights at each CV.SuperLearner iteration and summarize the distribution of those weights. This may be added to the SuperLearner package sometime in the future.
```{r}
# Review meta-weights (coefficients) from a CV.SuperLearner object
review_weights = function(cv_sl) {
meta_weights = coef(cv_sl)
means = colMeans(meta_weights)
sds = apply(meta_weights, MARGIN = 2, FUN = sd)
mins = apply(meta_weights, MARGIN = 2, FUN = min)
maxs = apply(meta_weights, MARGIN = 2, FUN = max)
# Combine the stats into a single matrix.
sl_stats = cbind("mean(weight)" = means, "sd" = sds, "min" = mins, "max" = maxs)
# Sort by decreasing mean weight.
sl_stats[order(sl_stats[, 1], decreasing = TRUE), ]
}
print(review_weights(cv_sl), digits = 3)
```
Notice that in this case the ensemble never uses the mean nor the randomForest with mtry = 1. Also the LASSO (glmnet) was only used on a subset of the folds. Adding multiple configurations of randomForest was helpful because mtry = 7 was used. However, based on the minimum column we can see that no algorithm was used every single time.
We recommend reviewing the weight distribution for any SuperLearner project to better understand which algorithms are chosen for the ensemble.
## Feature selection (screening)
When datasets have many covariates our algorithms may benefit from first choosing a subset of available covariates, a step called feature selection. Then we pass only those variables to the modeling algorithm, and it may be less likely to overfit to variables that are not related to the outcome.
Let’s revisit listWrappers() and check out the bottom section.
```{r}
listWrappers()
# Review code for corP, which is based on univariate correlation.
screen.corP
set.seed(1)
# Fit the SuperLearner.
# We need to use list() instead of c().
cv_sl = CV.SuperLearner(Y = y_train, X = x_train, family = binomial(),
# For a real analysis we would use V = 10.
V = 3,
parallel = "multicore",
SL.library = list("SL.mean", "SL.glmnet", c("SL.glmnet", "screen.corP")))
summary(cv_sl)
```
We see a small performance boost by first screening by univarate correlation with our outcome, and only keeping variables with a p-value less than 0.10. Try using some of the other screening algorithms as they may do even better for a particular dataset.
## Optimize for AUC
For binary prediction we are typically trying to maximize AUC, which can be the best performance metric when our outcome variable has some imbalance. In other words, we don’t have exactly 50% 1s and 50% 0s in our outcome. Our SuperLearner is not targeting AUC by default, but it can if we tell it to by specifying our method.
```{r}
set.seed(1)
cv_sl = CV.SuperLearner(Y = y_train, X = x_train, family = binomial(),
# For a real analysis we would use V = 10.
V = 3,
method = "method.AUC",
SL.library = list("SL.mean", "SL.glmnet", c("SL.glmnet", "screen.corP")))
## Loading required package: cvAUC
summary(cv_sl)
```
This conveniently shows us the AUC for each algorithm without us having to calculate it manually. But we aren’t getting SEs sadly.
Another important optimizer to consider is negative log likelihood, which is intended for binary outcomes and will often work better than NNLS (the default). This is specified by method = “NNloglik”.
## XGBoost hyperparameter exploration
XGBoost is a version of GBM that is even faster and has some extra settings. GBM’s adaptivity is determined by its configuration, so we want to thoroughly test a wide range of configurations for any given problem. Let’s do 27 now. This will take a good amount of time (~7 minutes on my computer) so we need to at least use multiple cores, if not multiple computers.
```{r}
# 3 * 3 * 3 = 27 different configurations.
# For a real analysis we would do 100, 500, or 1000 trees - this is just a demo.
tune = list(ntrees = c(10, 20, 50),
max_depth = 1:3,
shrinkage = c(0.001, 0.01, 0.1))
# Set detailed names = T so we can see the configuration for each function.
# Also shorten the name prefix.
learners = create.Learner("SL.xgboost", tune = tune, detailed_names = TRUE, name_prefix = "xgb")
# 27 configurations - not too shabby.
length(learners$names)
learners$names
# Confirm we have multiple cores configured. This should be > 1.
getOption("mc.cores")
# Remember to set multicore-compatible seed.
set.seed(1, "L'Ecuyer-CMRG")
# Fit the CV.SuperLearner.
system.time({
cv_sl = CV.SuperLearner(Y = y_train, X = x_train, family = binomial(),
# For a real analysis we would use V = 10.
V = 3,
parallel = "multicore",
SL.library = c("SL.mean", "SL.glmnet", learners$names, "SL.ranger"))
})
# Review results.
summary(cv_sl)
review_weights(cv_sl)
```
We can see how stochastic the weights are for each individual execution of SuperLearner.
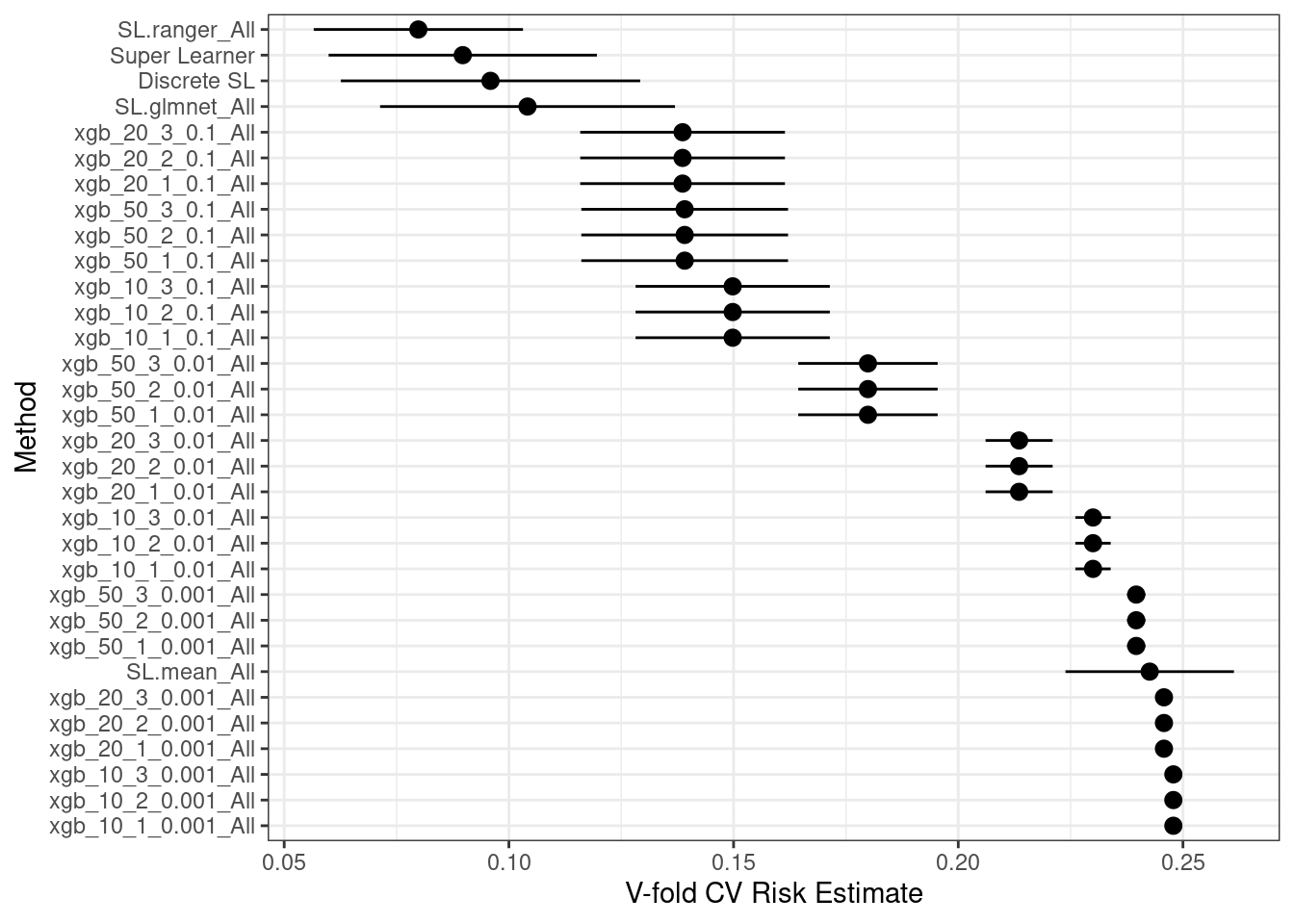
Finally, plot the performance for the different settings.
```{r}
plot(cv_sl) + theme_bw()
```
## Troubleshooting
If you get an error about predict for xgb.Booster, you probably need to install the latest version of XGBoost from github.