OLS regression From Scratch

OLS regression

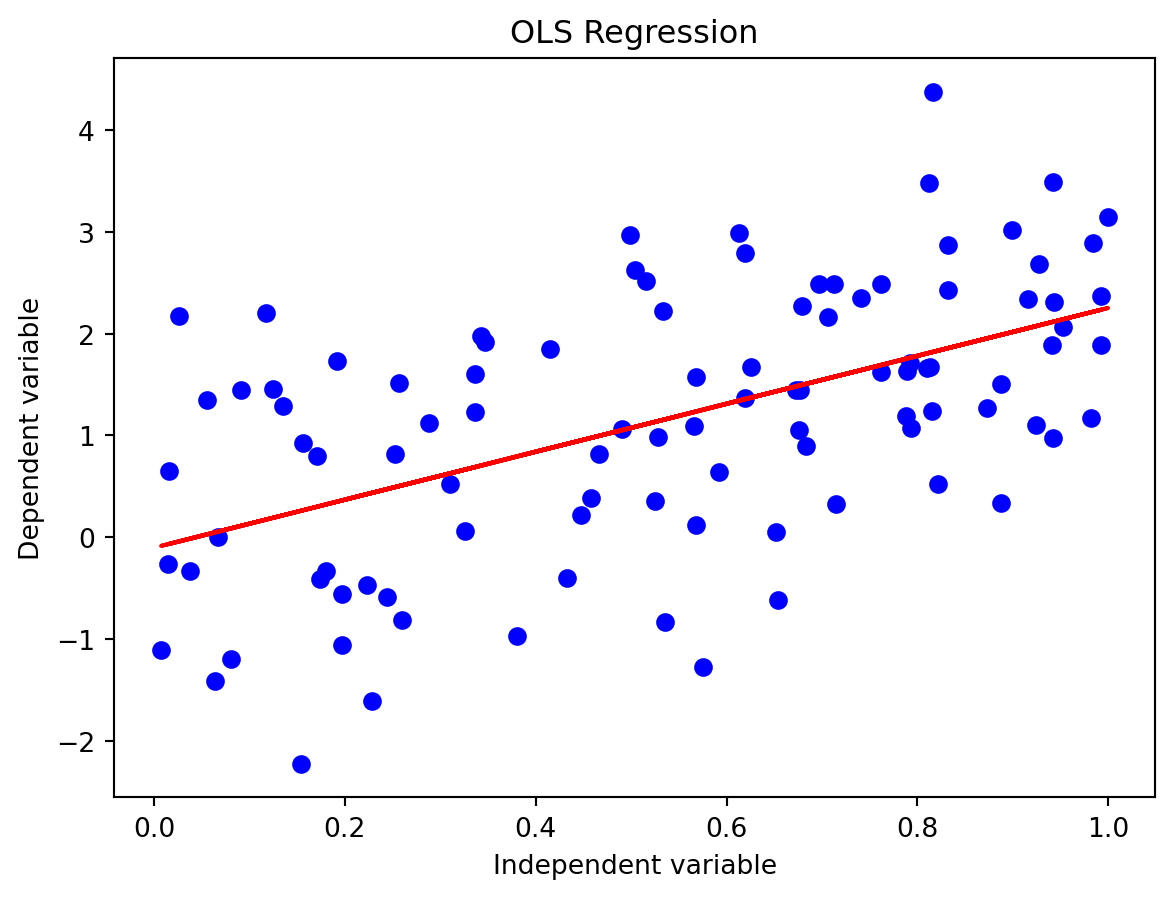
OLS regression is a method for estimating the parameters of a linear regression model. The goal is to find the line that best fits a set of data points. The line is represented by an equation of the form y = mx + b

where :

• y is the dependent variable,
• x is the independent variable,
• m is the slope of the line, and
• b is the y-intercept.

Generate random data

# Import the necessary libraries
import numpy as np
import pandas as pd

# Generate random data
n = 100
x = np.random.rand(n)
y = 2*x + np.random.normal(size=n)

# Create a DataFrame and save to CSV
df = pd.DataFrame({'x': x, 'y': y})
df.to_csv('your_dataset.csv', index=False)

import numpy as np
from numpy import ndarray
import pandas as pd
import xarray as xr
import matplotlib.pyplot as plt

# Step 1: Load the data and split into independent and dependent variables
data = pd.read_csv('your_dataset.csv')
X = data.iloc[:, :-1].values
y = data.iloc[:, -1].values

# add a column of 1s to the X matrix for the intercept term
X = np.append(arr=np.ones((len(X), 1)), values=X, axis=1)

# calculate the coefficients using the OLS formula
beta = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)

y_pred = X.dot(beta)

def mean_squared_error(y_true:ndarray, y_pred:ndarray):
    n = len(y_true)
    mse = sum([(y_true[i] - y_pred[i])**2 for i in range(n)]) / n
    return mse

def r2_score(y_true:ndarray, y_pred:ndarray):
    ssr = sum([(y_true[i] - y_pred[i])**2 for i in range(len(y_true))])
    sst = sum([(y_true[i] - np.mean(y_true))**2 for i in range(len(y_true))])
    r2 = 1 - (ssr / sst)
    return r2

rmse = np.sqrt(mean_squared_error(y, y_pred))
r2 = r2_score(y, y_pred)

print("RMSE: ", rmse)
print("R-squared: ", r2)

RMSE:  1.0862489887741527
R-squared:  0.29675681489500483

plt.scatter(X[:, 1], y, color='blue')
plt.plot(X[:, 1], y_pred, color='red')
plt.title('OLS Regression')
plt.xlabel('Independent variable')
plt.ylabel('Dependent variable')
plt.show()

Text(0.5, 1.0, 'OLS Regression')

Text(0.5, 0, 'Independent variable')

Text(0, 0.5, 'Dependent variable')