A garden of forking paths

couple of things

rethinking 💭 sequences

I’ve been thinking how to visualize learning the complex lewis games.

For states based on 0-1 sequences we can visualize the state space as a binary tree. Another way is the garden of forking paths.

The following code comes from Richard McElreath whose developed it for his book Statistical Rethinking. Hw used this code to to visualize the garden of forking paths. This is a very beautiful metaphor for explaining how Bayesian statistical models are built. The we build the garden by making independent picks from a random variable. The livlihood of some event. (e.g. at least three heads out of five.) are the paths that lead to such outcomes. And the probability is estimated by normalizing by the total number of possible paths.

The garden of forking paths is a way to visualize the state space of a sequence of binary choices. The code below is a modified version of the original code to allow for coloring of the paths. The code is written in R.

library(rethinking)

Loading required package: cmdstanr

This is cmdstanr version 0.8.1

- CmdStanR documentation and vignettes: mc-stan.org/cmdstanr

- CmdStan path: /home/oren/.cmdstan/cmdstan-2.34.1

- CmdStan version: 2.34.1

A newer version of CmdStan is available. See ?install_cmdstan() to install it.
To disable this check set option or environment variable cmdstanr_no_ver_check=TRUE.

Loading required package: posterior

This is posterior version 1.6.0

Attaching package: 'posterior'

The following objects are masked from 'package:stats':

    mad, sd, var

The following objects are masked from 'package:base':

    %in%, match

Loading required package: parallel

rethinking (Version 2.42)

Attaching package: 'rethinking'

The following object is masked from 'package:stats':

    rstudent

polar2screen <- function( dist, origin, theta ) {
  ## takes dist, angle and origin and returns x and y of destination point
  vx <- cos(theta) * dist;
  vy <- sin(theta) * dist;
  c( origin[1]+vx , origin[2]+vy );
}

screen2polar <- function( origin, dest ) {
  ## takes two points and returns distance and angle, from origin to dest
  vx <- dest[1] - origin[1];
  vy <- dest[2] - origin[2];
  dist <- sqrt( vx*vx + vy*vy );
  theta <- asin( abs(vy) / dist );
  ## correct for quadrant
  if( vx < 0 && vy < 0 ) theta <- pi + theta; # lower-left
  if( vx < 0 && vy > 0 ) theta <- pi - theta; # upper-left
  if( vx > 0 && vy < 0 ) theta <- 2*pi - theta; # lower-right
  if( vx < 0 && vy==0 ) theta <- pi;
  if( vx==0 && vy < 0 ) theta <- 3*pi/2; 
  ## return angle and dist
  c( theta, dist );
}

point.polar <- function(dist,theta,origin=c(0,0),...) {
    # angle theta is in radians
    pt <- polar2screen(dist,origin,theta)
    points( pt[1] , pt[2] , ... )
    invisible( pt )
}

line.polar <- function(dist,theta,origin=c(0,0),...) {
    # dist should be vector of length 2 with start and end points
    # theta is angle
    pt1 <- polar2screen(dist[1],origin,theta)
    pt2 <- polar2screen(dist[2],origin,theta)
    lines( c(pt1[1],pt2[1]), c(pt1[2],pt2[2]) , ... )
}

line.short <- function(x,y,short=0.1,...) {
    # shortens the line segment, but retains angle and placement
    pt1 <- c(x[1],y[1])
    pt2 <- c(x[2],y[2])
    theta <- screen2polar( pt1 , pt2 )[1]
    dist <- screen2polar( pt1 , pt2 )[2]
    q1 <- polar2screen( short , pt1 , theta )
    q2 <- polar2screen( dist-short , pt1 , theta )
    lines( c(q1[1],q2[1]) , c(q1[2],q2[2]) , ... )
}

wedge <- function(dist,start,end,pt,hedge=0.1,alpha,lwd=2,...) {
    # start: start angle of wedge
    # end: end angle of wedge
    # pt: vector of point bg colors
    n <- length(pt)
    points.save <- matrix(NA,nrow=n,ncol=2) # x,y columns
    span <- abs(end-start)
    span2 <- span*(1 - 2*hedge)
    origin <- start + span*hedge
    gap <- span2/n
    theta <- origin + gap/2
    border <- rep("black",length(pt))
    if ( !missing(alpha) ) {
        pt <- sapply( 1:length(pt) , function(i) col.alpha(pt[i],alpha[i]) )
        border <- sapply( 1:length(pt) , function(i) col.alpha(border[i],alpha[i]) )
    }
    for ( i in 1:n ) {
        points.save[i,] <- point.polar( dist , theta , pch=21 , lwd=lwd , bg=pt[i] , col=border[i] , ... )
        theta <- theta + gap
    }
    points.save
}

#######
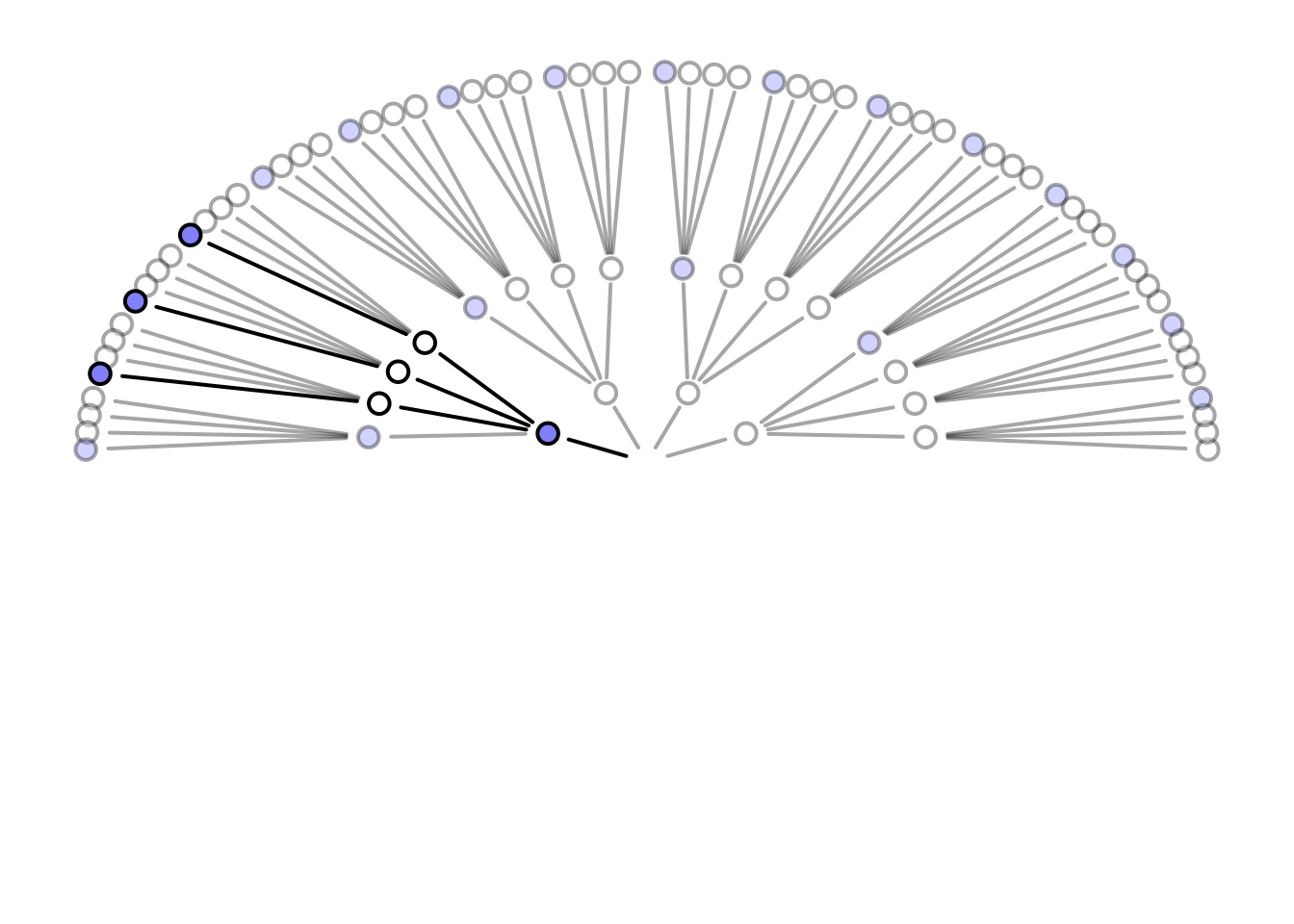
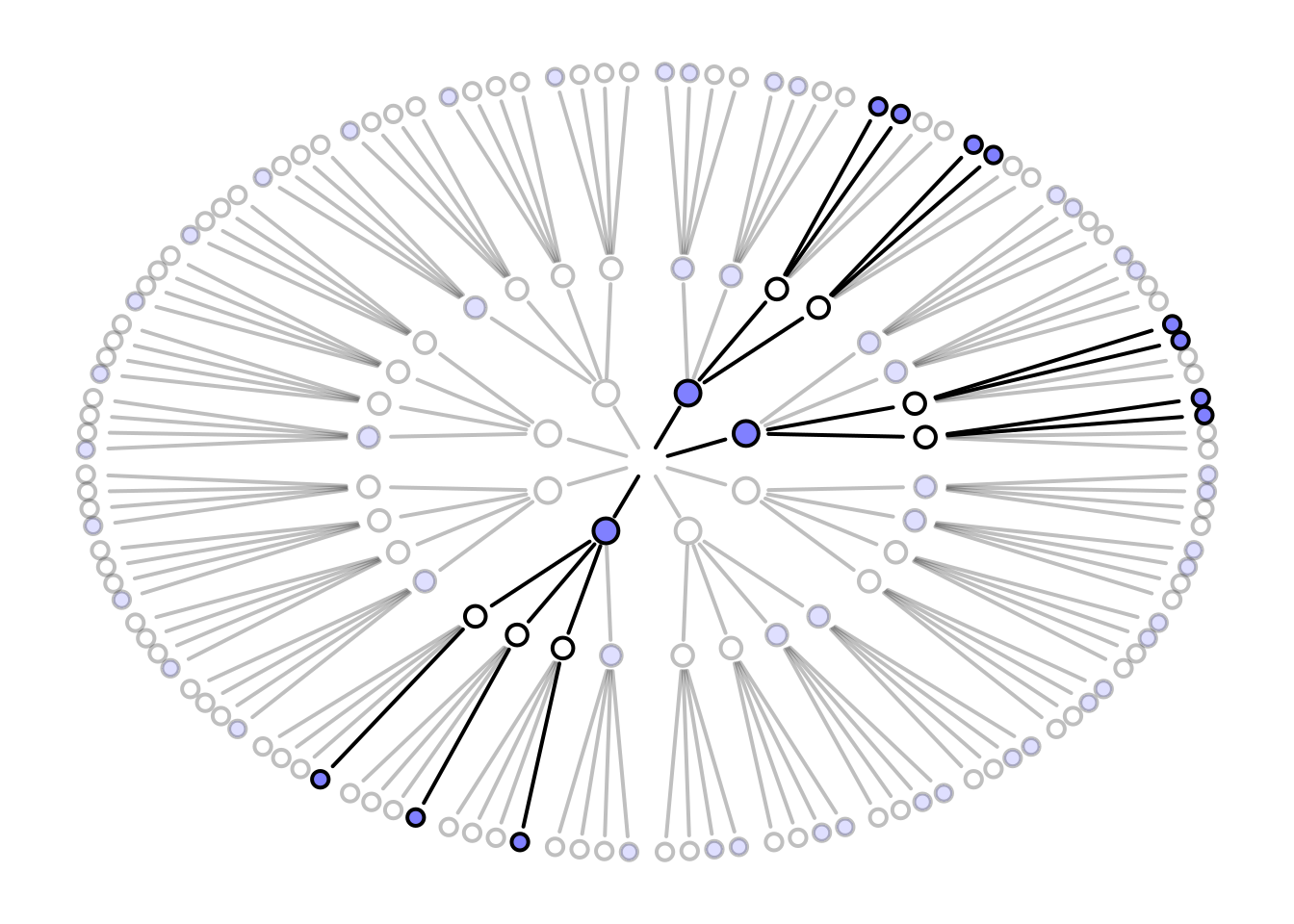
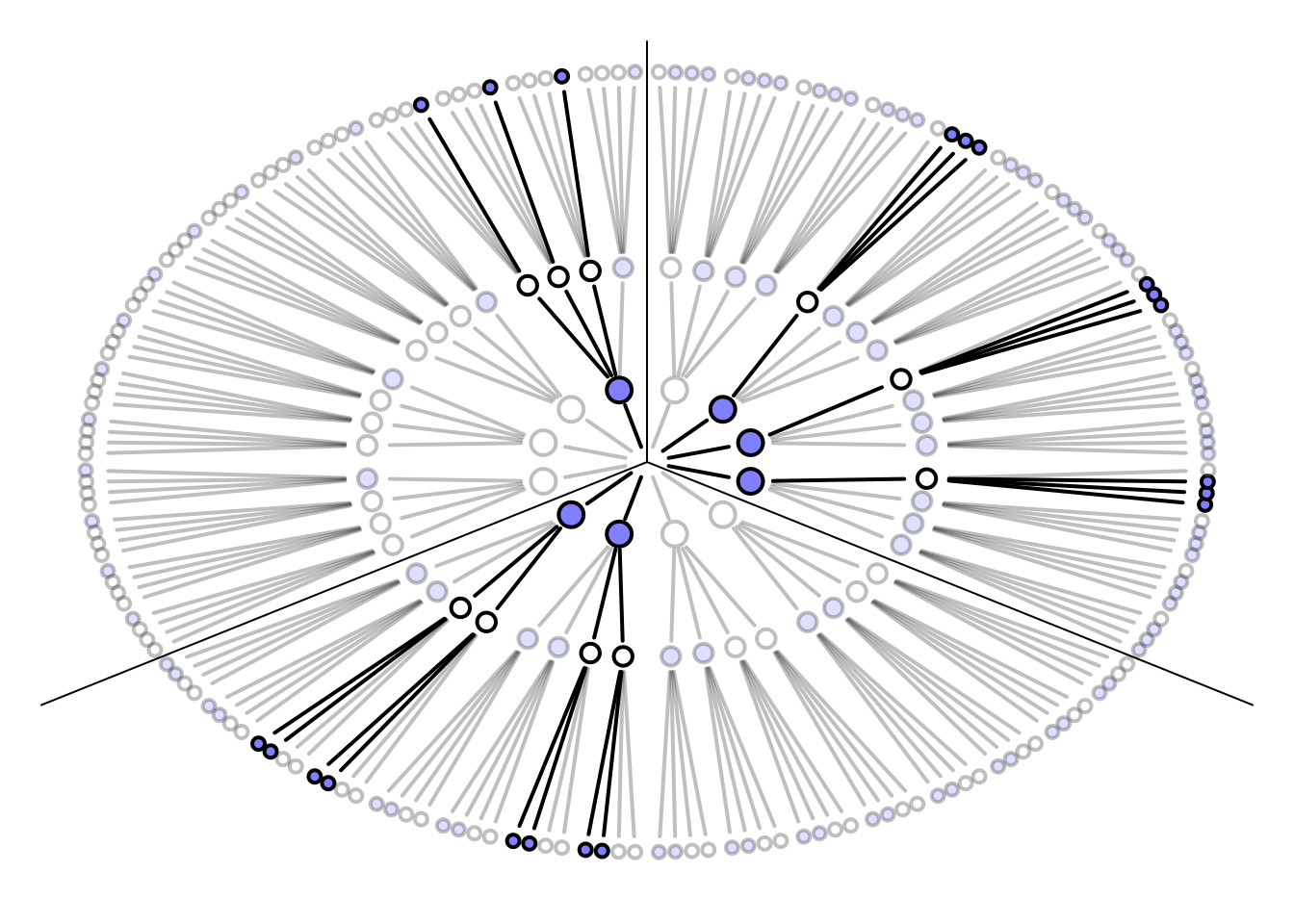
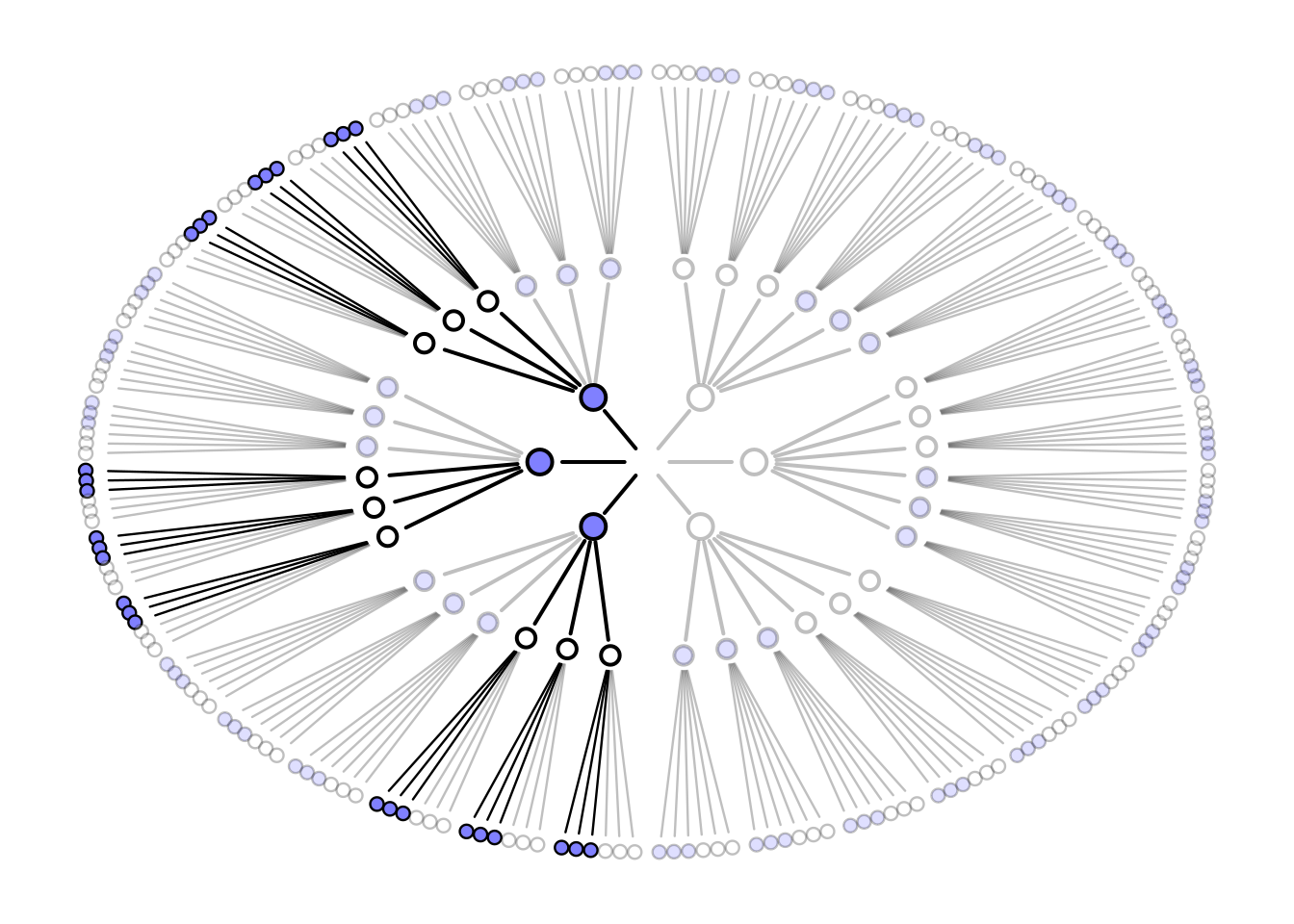
# garden draws paths using recursion

garden <- function( arc , possibilities , data , alpha.fade = 0.25 , hedge=0.1 , hedge1=0 , newplot=TRUE , plot.origin=FALSE , cex=1.5 , lwd=2 , adj.cex , adj.lwd , ring_dist , ... ) {
    
    poss.cols <- ifelse( possibilities==1 , rangi2 , "white" )
    
    if ( missing(adj.cex) ) adj.cex=rep(1,length(data))
    if ( missing(adj.lwd) ) adj.lwd=rep(1,length(data))
    
    if ( newplot==TRUE ) {
    # empty plot
        par(mgp = c(1.5, 0.5, 0), mar = c(1, 1, 1, 1) + 0.1, tck = -0.02)
        plot( NULL , xlim=c(-1,1) , ylim=c(-1,1) , bty="n" , xaxt="n" , yaxt="n" , xlab="" , ylab="" )
    }
    
    if ( plot.origin==TRUE ) point.polar( 0 , 0 , pch=16 )
    
    N <- length(data)
    n_poss <- length(possibilities)
    
    # draw rings
    
    # compute distance out for each ring
    # use golden ratio 1.618 for each successive ring
    goldrat <- 1.618
    if ( missing(ring_dist) ) {
        ring_dist <- rep(1,N)
        if ( N>1 )
            for ( i in 2:N ) ring_dist[i] <- ring_dist[i-1]*goldrat
        ring_dist <- ring_dist / sum(ring_dist)
        ring_dist <- cumsum(ring_dist)
    }
    
    if ( length(alpha.fade)==1 ) alpha.fade <- rep(alpha.fade,N)
    
    draw_wedge <- function(r,hit_prior,arc2,hedge=0.1,hedge1=0,lines_to) {
    
        # is each path clear?
        hit <- hit_prior * ifelse( possibilities==data[r] , 1 , 0 )
        
        # transparency for blocked paths
        alpha <- ifelse( hit , 1 , alpha.fade[r] )
        
        # draw wedge
        hedge_use <- ifelse( r==1 , hedge1 , hedge )
        pts <- wedge( ring_dist[r] , arc2[1] , arc2[2] , poss.cols , hedge=hedge_use , alpha=alpha , cex=cex*adj.cex[r] , lwd=lwd*adj.lwd[r] )
        
        if ( N > r ) {
            # draw next layer
            span <- abs( arc2[1] - arc2[2] ) / n_poss
            for ( j in 1:n_poss ) {
                # for each possibility, draw the next wedge
                # recursion handles deeper wedges
                new_arc <- c( arc2[1]+span*(j-1) , arc2[1]+span*j )
                pts2 <- draw_wedge(r+1,hit[j],new_arc,hedge,lines_to=pts[j,])
            }#j
        }# N>r
        
        # draw lines back to parent point
        if ( !missing(lines_to) ) {
            for ( k in 1:n_poss ) {
                alpha_l <- ifelse( hit==1 , 1 , alpha.fade[r] )
                line.short( c(lines_to[1],pts[k,1]) , c(lines_to[2],pts[k,2]) , lwd=lwd*adj.lwd[r] , short=0.04 , col=col.alpha("black",alpha_l[k]) )
            }
        } # lines_to
        
        return(pts)
        
    }
    
    pts1 <- draw_wedge(1,1,arc=arc,hedge=hedge,lines_to=c(0,0))
    
    invisible(pts1)
    
}


##

goldrat <- 1.618
ring_dist <- rep(1,3)
for ( i in 2:3 ) ring_dist[i] <- ring_dist[i-1]*goldrat
ring_dist <- ring_dist / sum(ring_dist)
ring_dist <- cumsum(ring_dist)

dat <- c(1,0,1)

arc <- c( 0 , pi )
garden(
    arc = arc,
    possibilities = c(0,0,0,1),
    data = dat,
    hedge = 0.05,
    ring_dist=ring_dist,
    alpha.fade=0.35
)

####
# compare {1,0,0,0}, {1,1,0,0} and {1,1,1,0}

dat <- c(1,0,1)

arc <- c( 0 , pi )
garden(
    arc = arc,
    possibilities = c(0,0,0,1),
    data = dat,
    hedge = 0.05,
    ring_dist=ring_dist,
    alpha.fade=0.35
)


####
# second plot
# compare {1,0,0,0} to {1,1,1,0}

dat <- c(1,0,1)

arc <- c( pi/2 , pi/2+pi )
garden(
    arc = arc,
    possibilities = c(0,0,0,1),
    data = dat,
    hedge = 0.05,
    adj.cex=c(1.2,1,0.8)
)

arc <- c( arc[2] , arc[2] + pi )
garden(
    arc = arc,
    possibilities = c(0,0,1,1),
    data = dat,
    hedge = 0.05,
    newplot=FALSE,
    adj.cex=c(1.2,1,0.8)
)

####
# third plot
# three options: {1,0,0,0}, {1,1,0,0}, {1,1,1,0}

dat <- c(1,0,1)
ac <- c(1.2,0.9,0.6)

arc <- c( pi/2 , pi/2 + (2/3)*pi )
garden(
    arc = arc,
    possibilities = c(1,0,0,0),
    data = dat,
    hedge = 0.05,
    adj.cex=ac
)

arc <- c( arc[2] , arc[2] + (2/3)*pi )
garden(
    arc = arc,
    possibilities = c(1,1,0,0),
    data = dat,
    hedge = 0.05,
    newplot=FALSE,
    adj.cex=ac
)

arc <- c( arc[2] , arc[2] + (2/3)*pi )
garden(
    arc = arc,
    possibilities = c(1,1,1,0),
    data = dat,
    hedge = 0.05,
    newplot=FALSE,
    adj.cex=ac
)

line.polar( c(0,2) , pi/2 , lwd=1 )
line.polar( c(0,2) , pi/2 + (2/3)*pi , lwd=1 )
line.polar( c(0,2) , pi/2 + 2*(2/3)*pi , lwd=1 )

#####
# single possibility out of 10 plot

dat <- c(1,0,1)
ac <- c(1.2,0.9,0.65)
al <- c(1,1,0.6)

n <- 6
nblue <- 3

arc <- c( pi/2 , pi/2 + 2*pi )
garden(
    arc = arc,
    possibilities = c(rep(1,nblue),rep(0,n-nblue)),
    data = dat,
    hedge = 0.05,
    adj.cex=ac,
    adj.lwd=al
)

Further work

• todo: make figures with binary nodes
• todo: extend to a series of 4
• todo: highlight a subset of paths with a different color
• show corresponding truth tables.