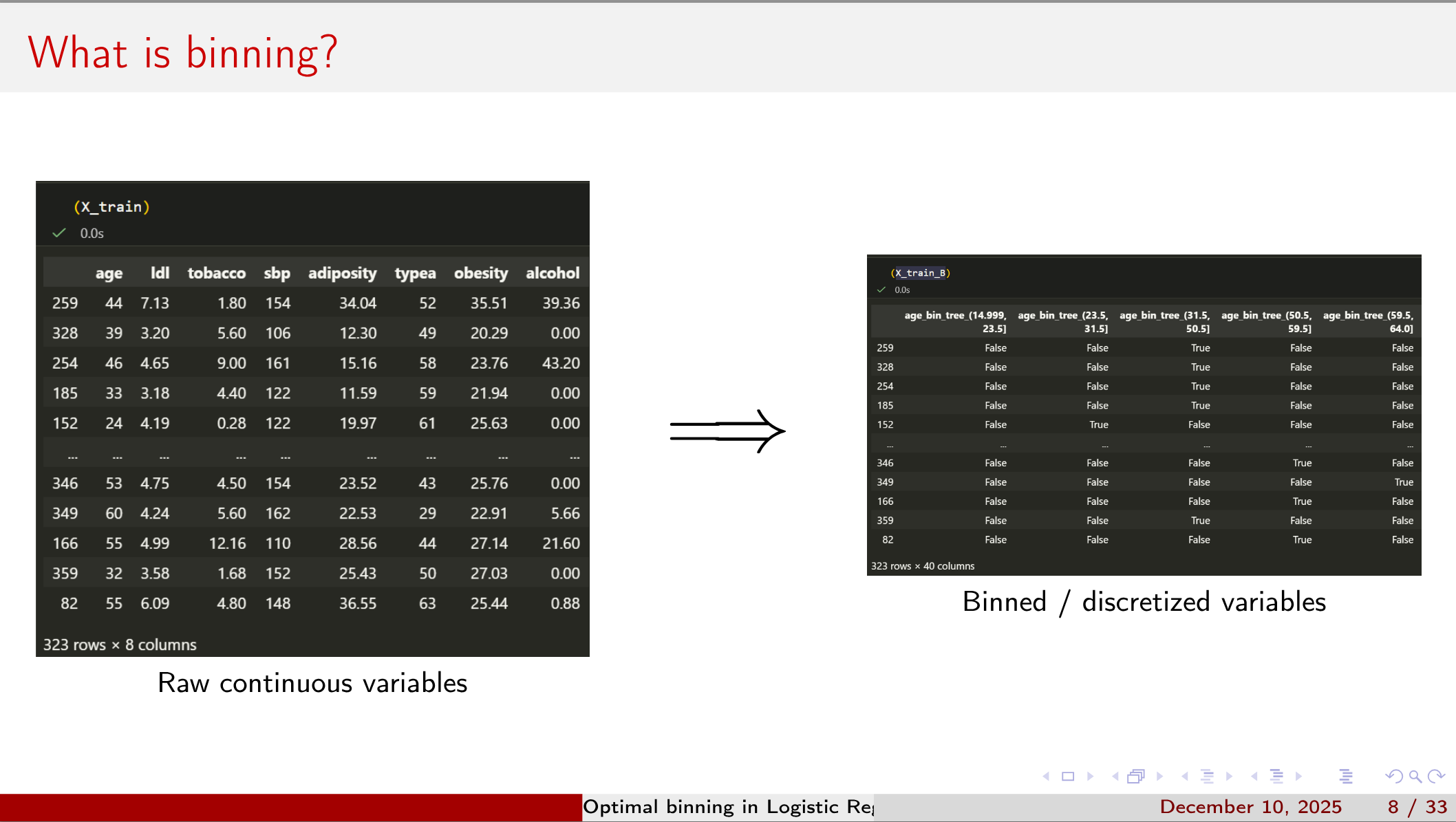
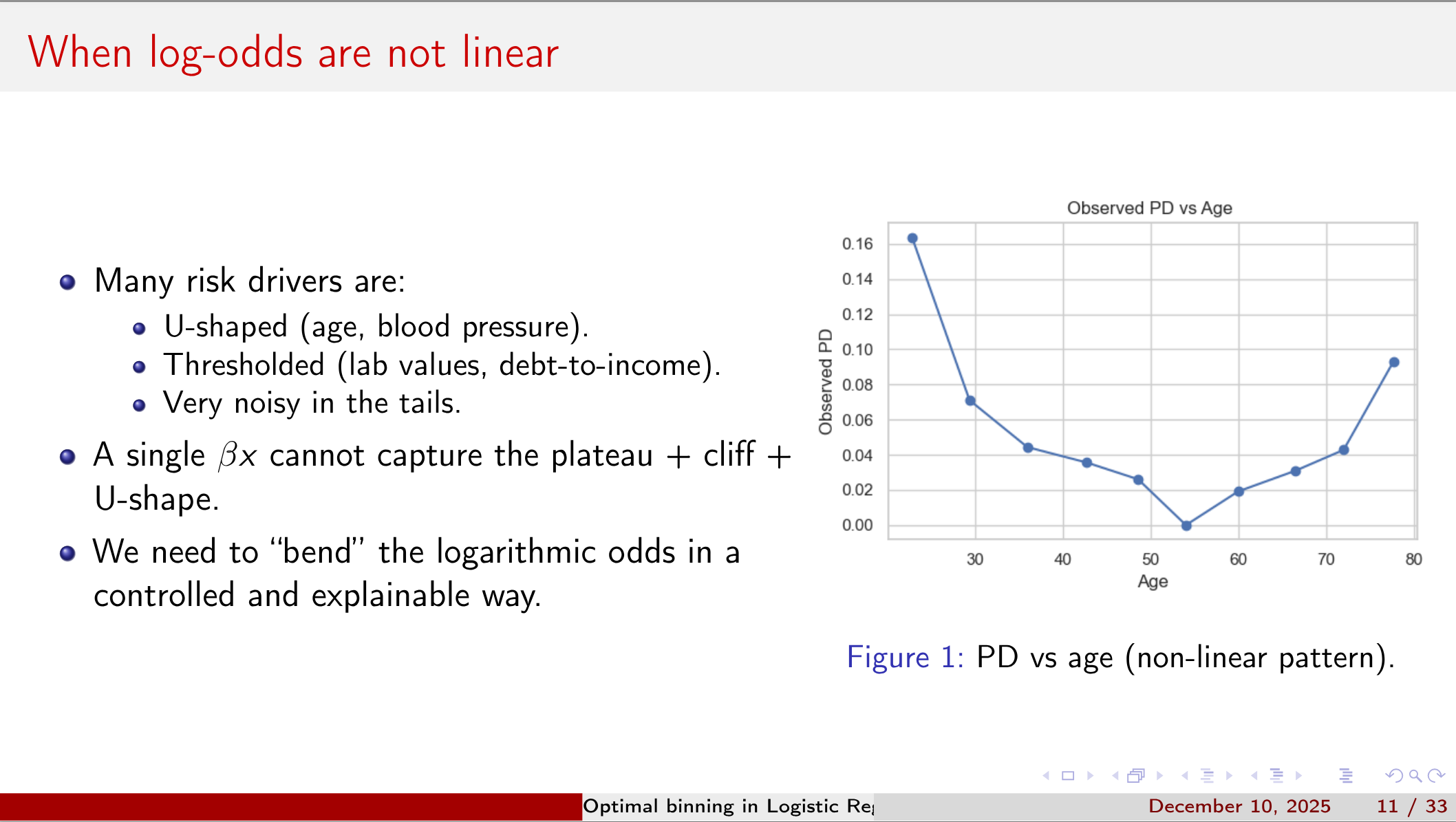
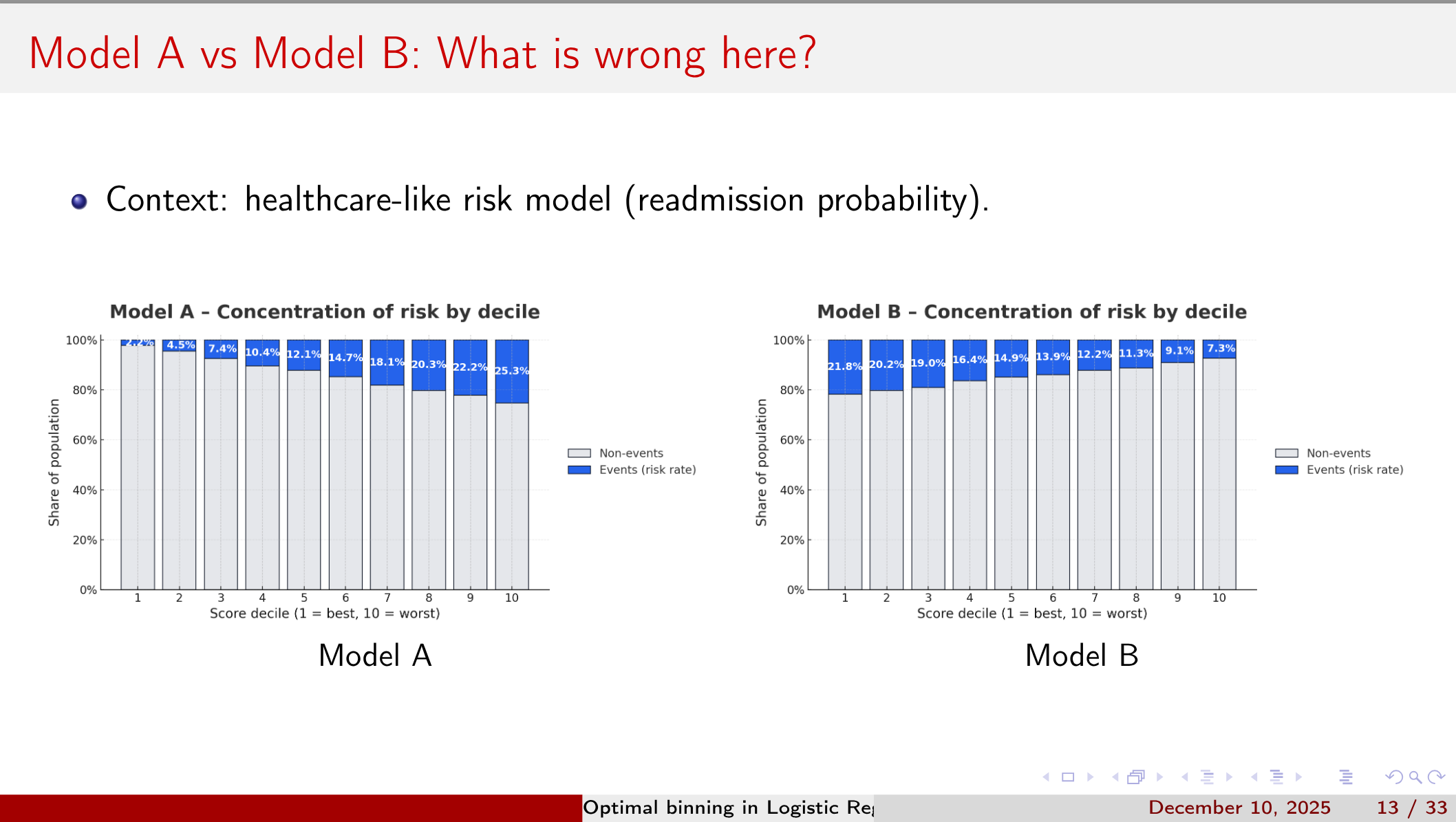
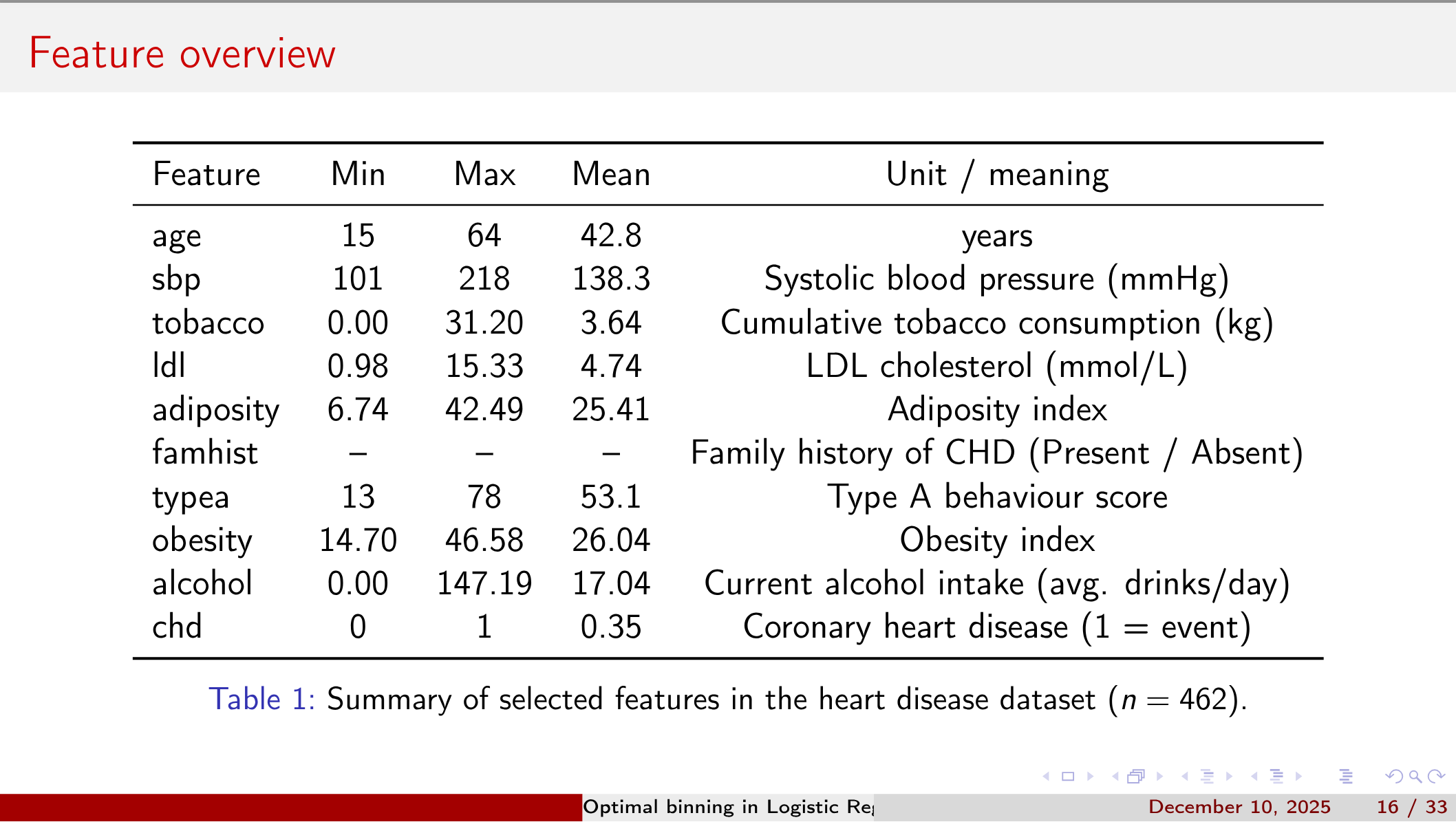
In many regulated industries—finance, healthcare, insurance—logistic regression remains the model of choice for its interpretability and regulatory acceptability.
Yet capturing non-linear effects and interactions often requires variable binning, and naive approaches (equal-width or quantile cuts) can either wash out signal or invite overfitting.
In this 30-minute session, data scientists and risk analysts with a working knowledge of logistic regression and Python will learn to:
- Diagnose the weaknesses of basic binning strategies.
- Select and apply optimal-binning algorithms for different use cases.
- Assess bin stability and guard against model overfit.
All code, data samples, and a notebook will be available on GitHub.
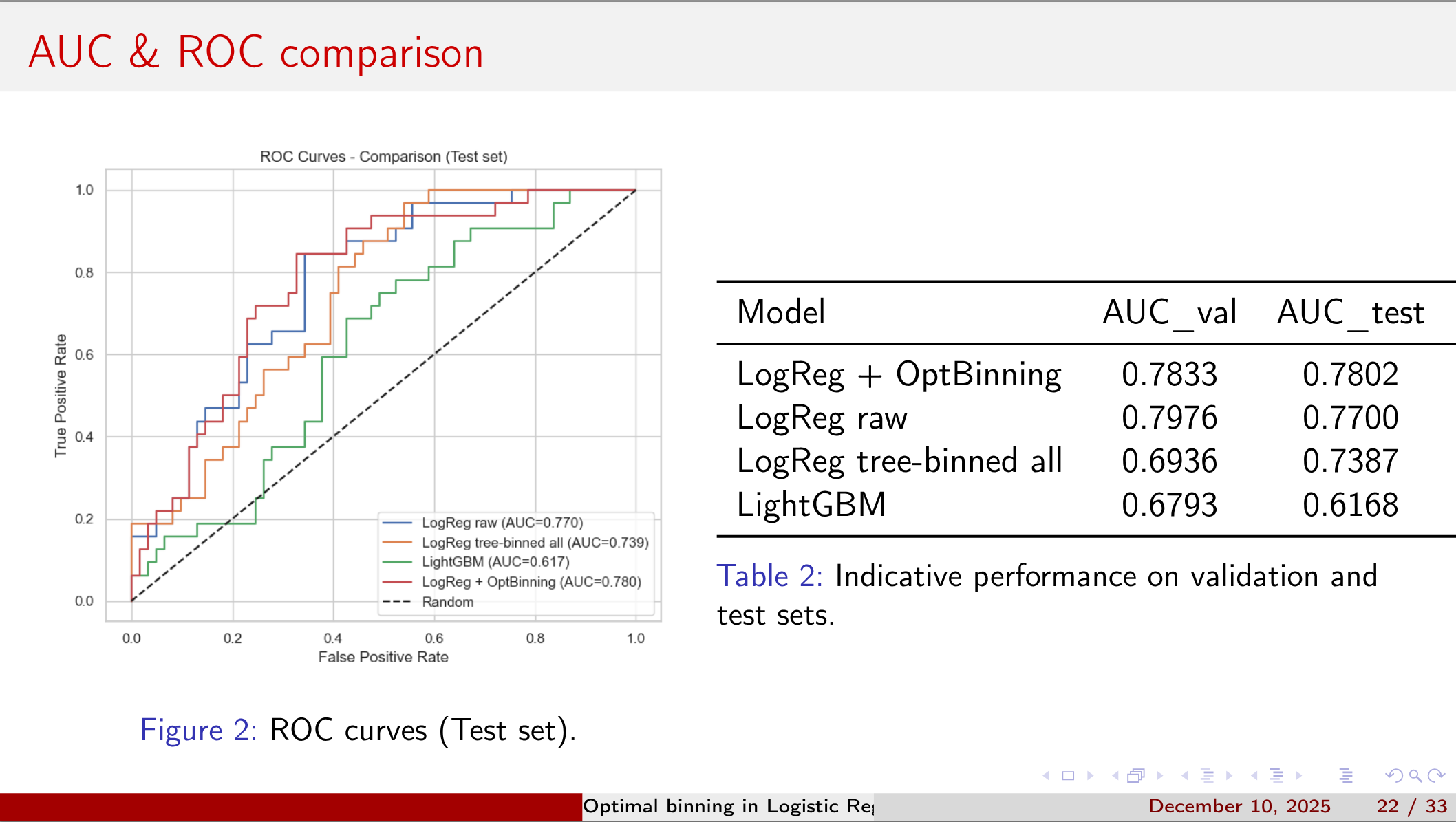
Despite the rise of complex “black-box” models, regulated environments still demand transparency. Properly binned variables not only improve model fit but also yield coefficients that the business and auditors can interpret.
However, determining cut-points that preserve true signal while avoiding data-snooping bias is non-trivial.
- Understand the basic idea behind binning (the what)
- To know in which contexts variable binning makes sense (the when and why).
- Choose among popular optimal-binning techniques (e.g., ChiMerge, MDLP, decision-tree-based) based on data size, feature type, and operational constraints (the how).
- Data scientists and risk analysts who use logistic regression in regulated settings and need a reproducible, explainable feature-engineering pipeline.
- Prerequisites: Basic Python (pandas, scikit-learn) and logistic-regression familiarity
- Materials: GitHub repo with notebook, data samples, will be shared during the talk
Charaf Zguiouar
Quantitative Finance and Econometrics Gradutate from Sorbonne’s University. Currently working as Data Scientist at BNP Paribas & as lecturer at Sorbonne’s University.
Outline
Weight of Evidence (WoE) and Information Value (IV) are two key concepts in variable binning for logistic regression.
WoE_j = \ln\left(\frac{Good_j / Total\ Good}{Bad_j / Total\ Bad }\right) \tag{1}
IV = \sum_j \left(\frac{Good_j}{Total\ Good} - \frac{Bad_j}{Total\ Bad}\right) \times WoE_j \tag{2}
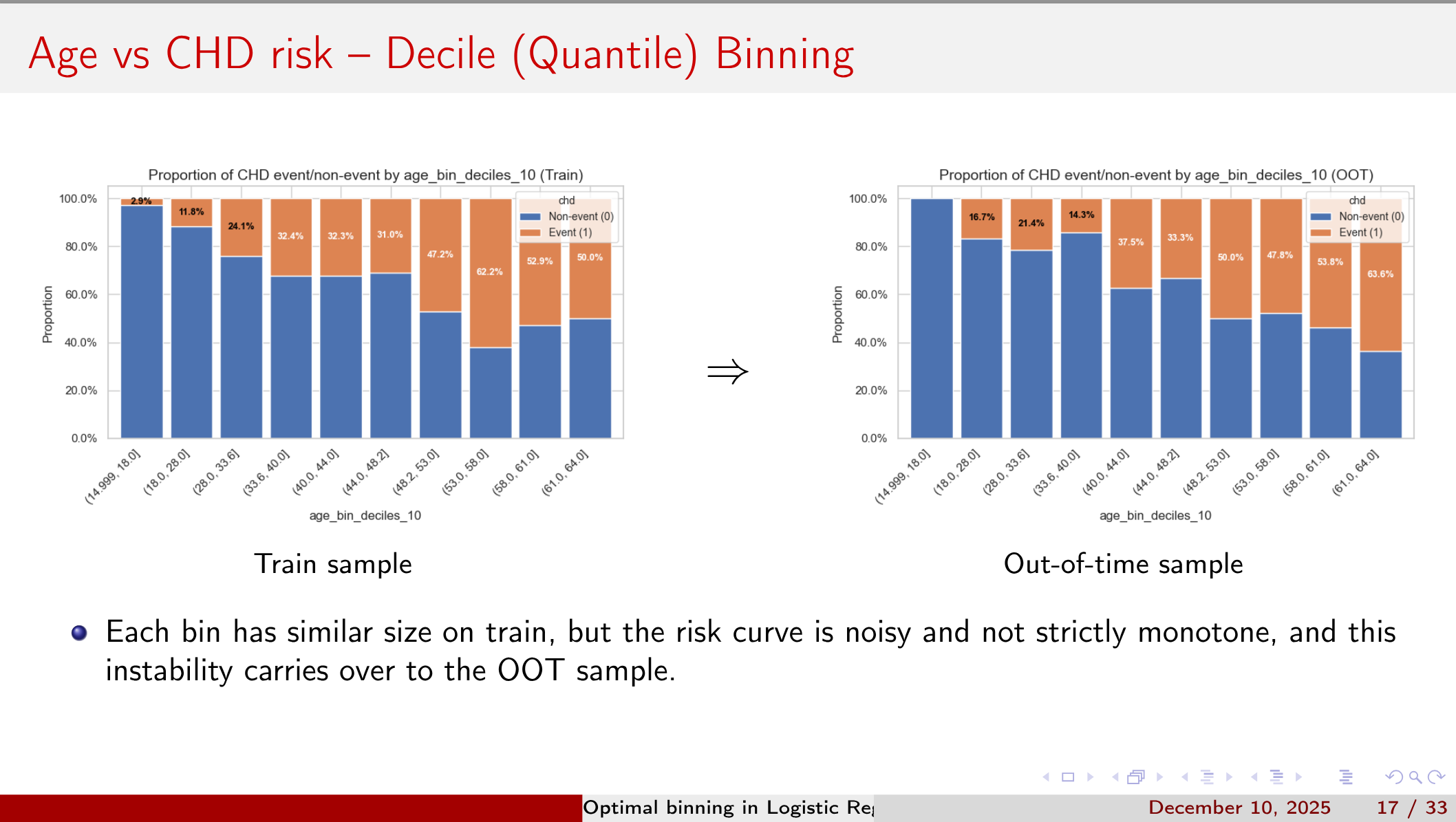
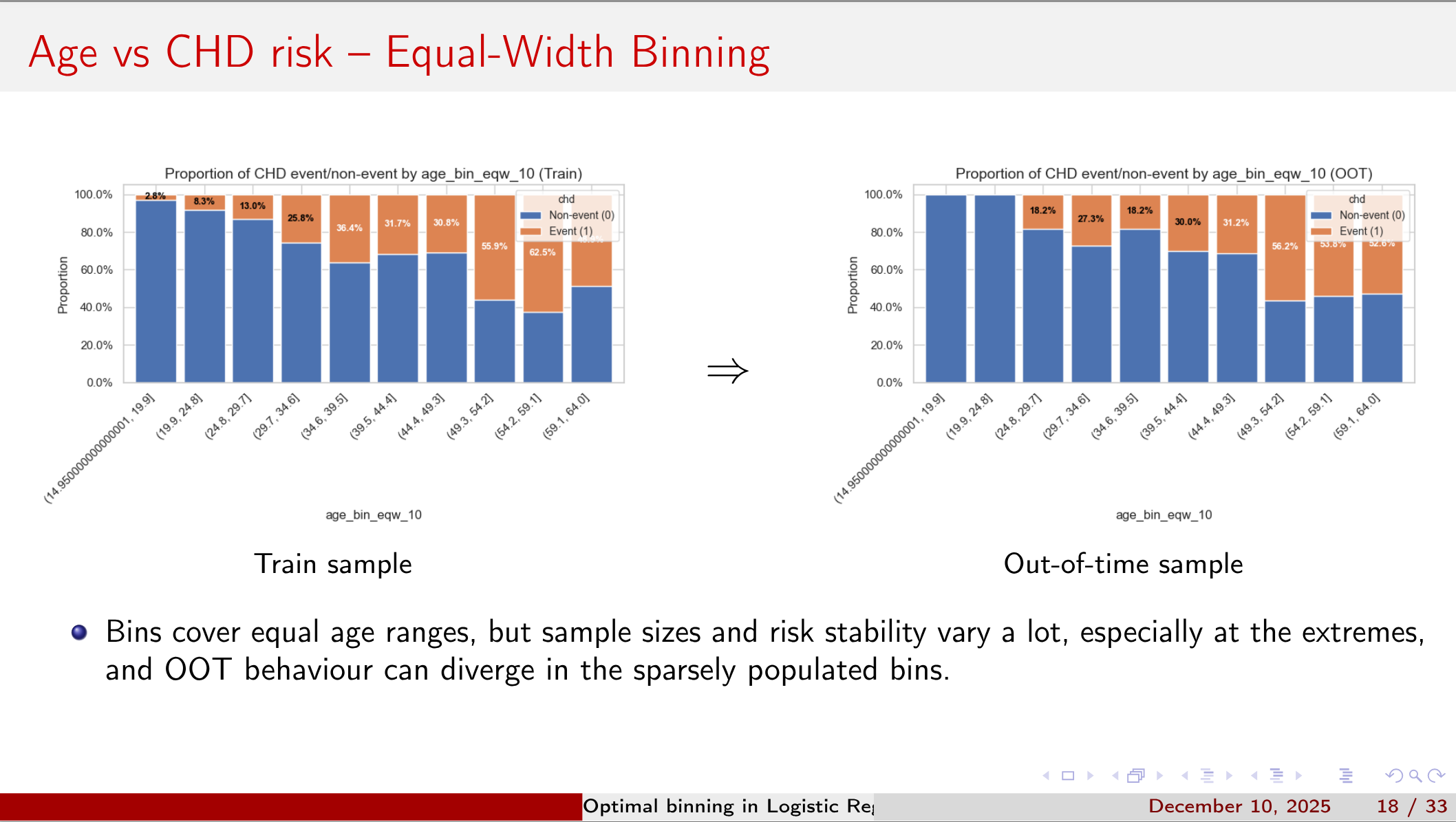
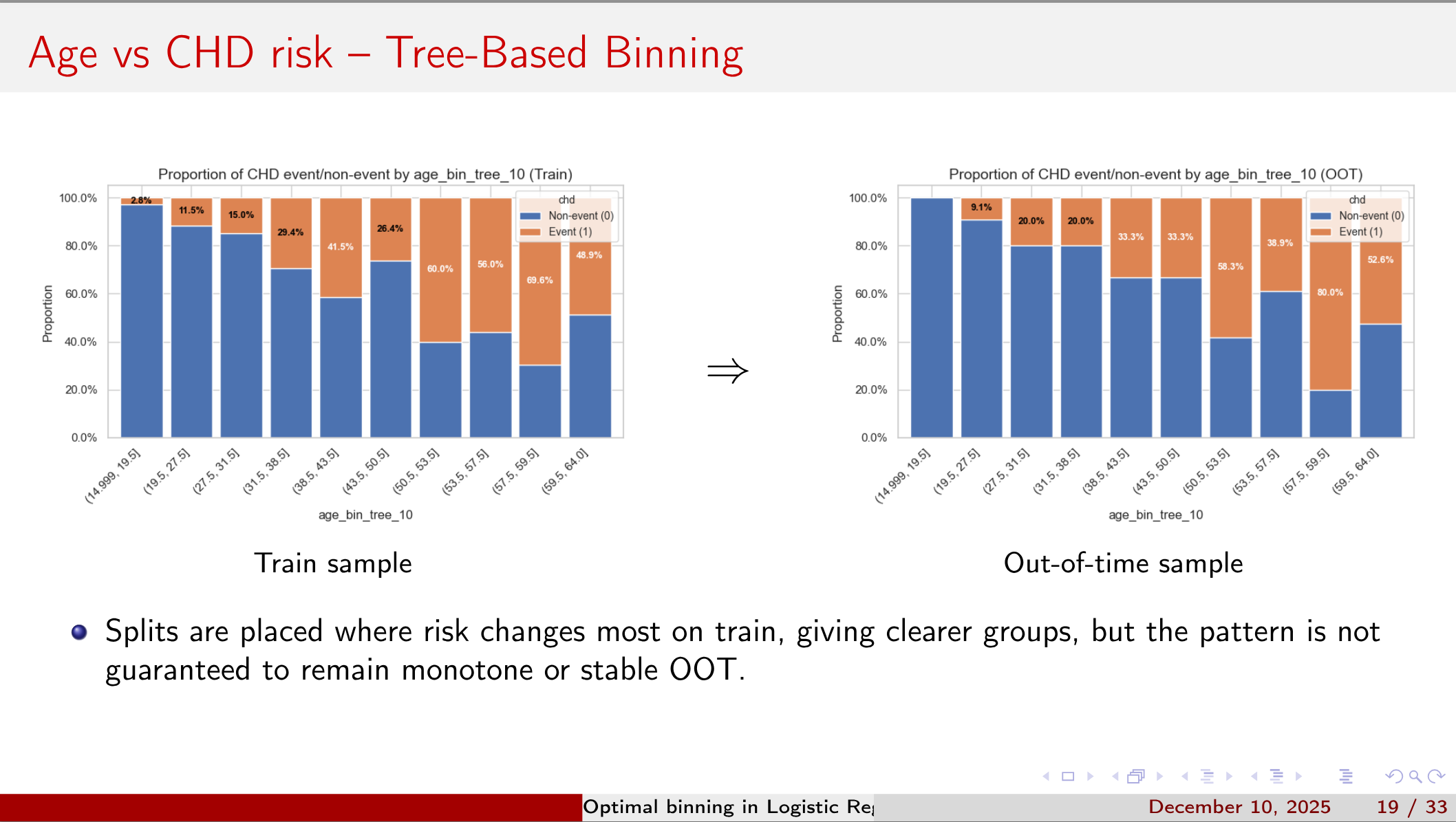
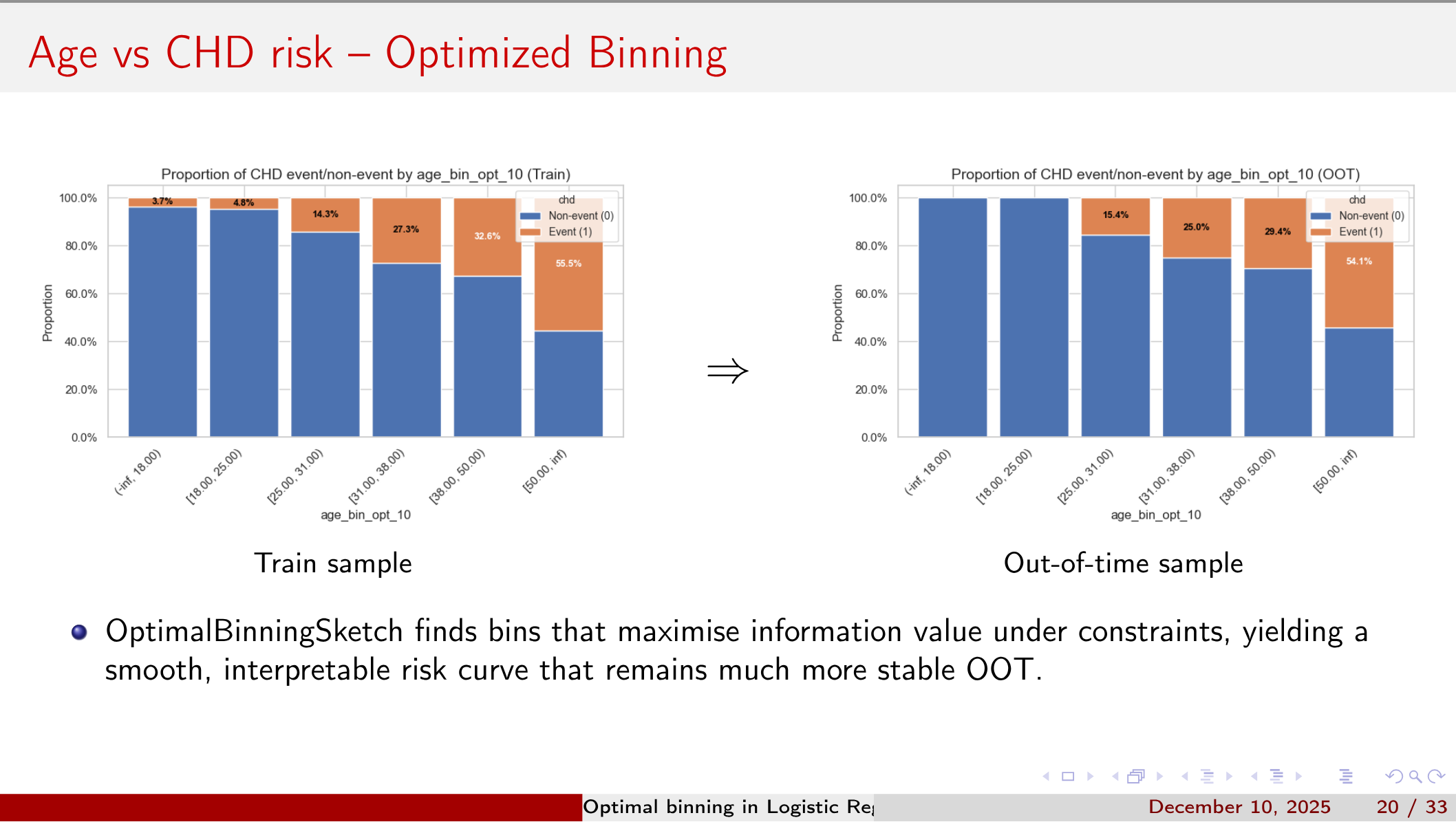
Four Binning Strategies
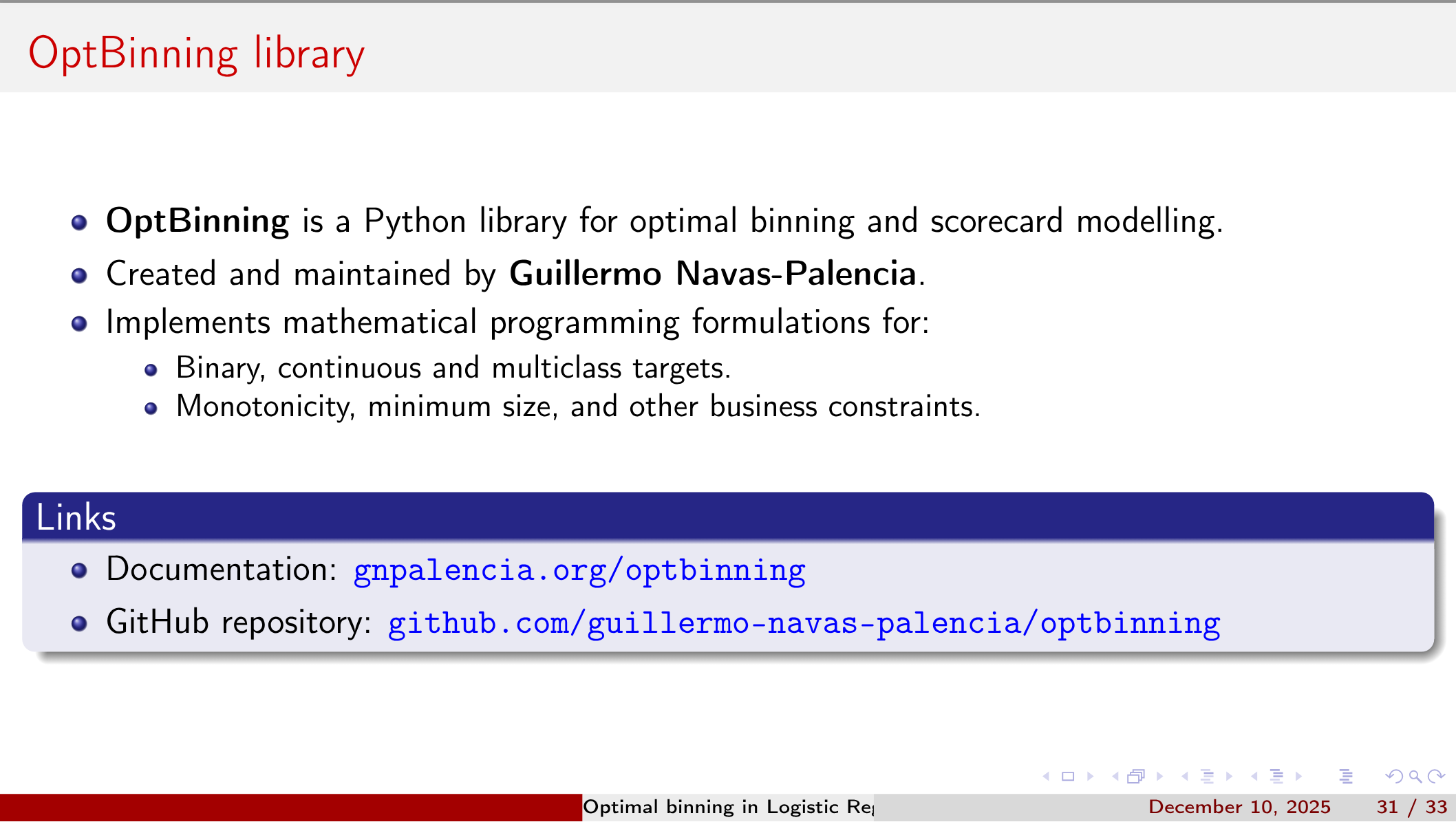
- OptBinning is a Python library for optimal binning and scorecard modelling.
- Created and maintained by Guillermo Navas-Palencia.
- Implements mathematical programming formulations for:
- Binary, continuous and multiclass targets.
- Monotonicity, minimum size, and other business constraints
- Documentation: gnpalencia.org/optbinningGitHub
- repository: github.com/guillermo-navas-palencia/optbinning
Reflection
We looked at what we mean by binning in Logistic Regression, why and when to use it, and how to choose an optimal binning technique based on data and operational constraints.
We also saw how to implement these techniques in Python using the OptBinning library.
Citation
@online{bochman2025,
author = {Bochman, Oren},
title = {Optimal {Variable} {Binning} in {Logistic} {Regression}},
date = {2025-12-10},
url = {https://orenbochman.github.io/posts/2025/2025-12-10-pydata-optimal-binning-in-logistic-regression/},
langid = {en}
}