Deep Neural Networks - Notes for Lesson 16

{{< pdf lec16.pdf width="100%" class="ppSlide" >}}

Lecture 16a Learning a joint model of images and captions

Modeling the joint density of images and captions

(Srivastava and Salakhutdinov, NIPS 2012)

• Goal: To build a joint density model of captions and standard computer vision feature vectors extracted from real photographs.
  • This needs a lot more computation than building a joint density model of labels and digit images!

1. Train a multilayer model of images.
2. Train a separate multilayer model of word-count vectors.
3. Then add a new top layer that is connected to the top layers of both individual models.
   • Use further joint training of the whole system to allow each modality to improve the earlier layers of the other modality.

• Instead of using a deep belief net, use a deep Boltzmann machine that has symmetric connections between all pairs of layers.
  • Further joint training of the whole DBM allows each modality to improve the earlier layers of the other modality.
  • That’s why they used a DBM.
  • They could also have used a DBN and done generative fine-tuning with contrastive wake-sleep.
• But how did they pre-train the hidden layers of a deep Boltzmann Machine?
  • Standard pre-training leads to composite model that is a DBN not a DBM.

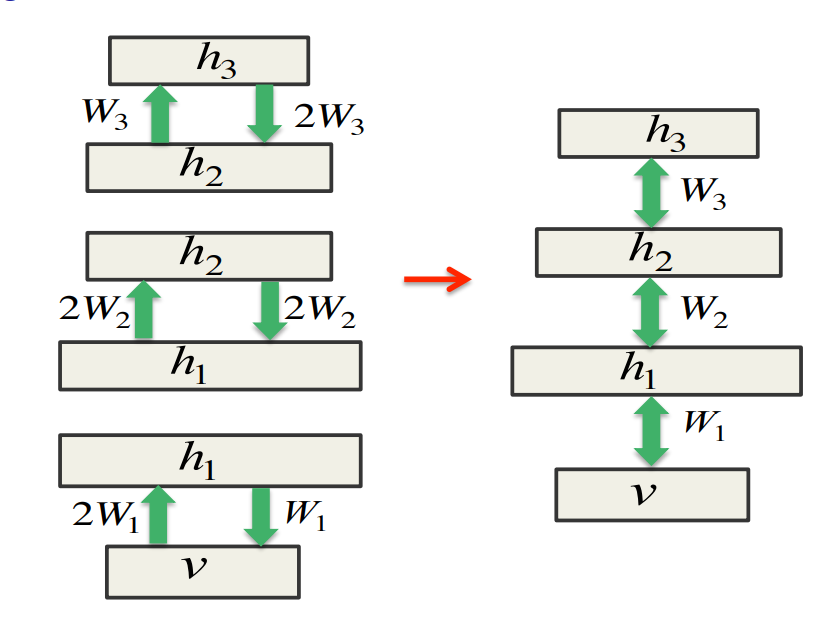
Combining three RBMs to make a DBM

Combining RBMs into a DBM

• The top and bottom RBMs must be pretrained with the weights in one direction twice as big as in the other direction.
  • This can be justified!
• The middle layers do geometric model averaging.

Lecture 16b - Hierarchical coordinate frames

Why convolutional neural networks are doomed

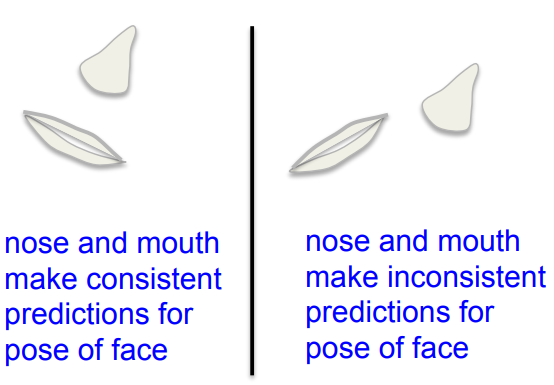
• Pooling loses the precise spatial relationships between higher-level parts such as a nose and a mouth.
  • The precise spatial relationships are needed for identity recognition.
  • Overlapping the pools helps a bit.
• Convolutional nets that just use translations cannot extrapolate their understanding of geometric relationships to radically new viewpoints.
  • People are very good at extrapolating. After seeing a new shape once they can recognize it from a different viewpoint.

The hierarchical coordinate frame approach

hierarchical frames

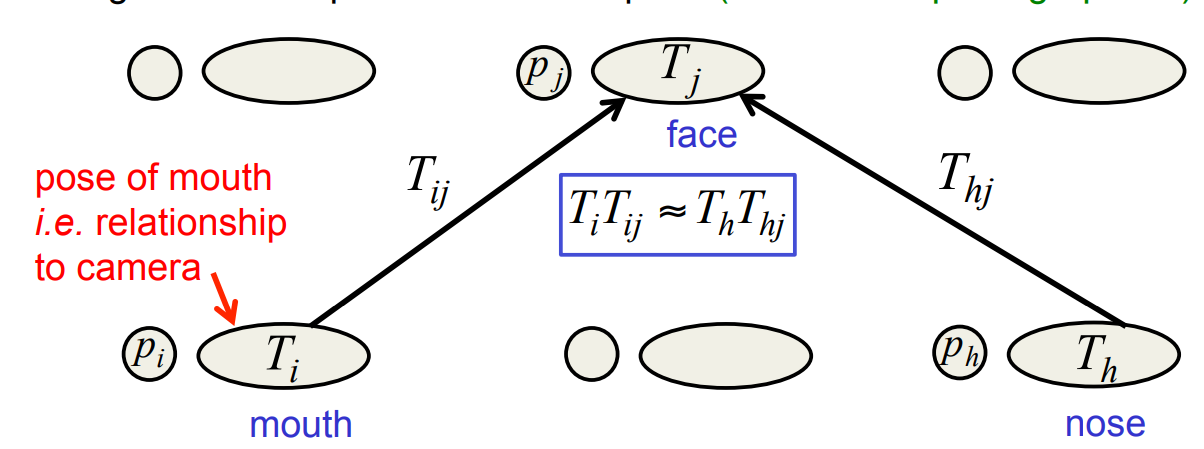
• Use a group of neurons to represent the conjunction of the shape of a feature and its pose relative to the retina.
  • The pose relative to the retina is the relationship between the coordinate frame of the retina and the intrinsic coordinate frame of the feature.
• Recognize larger features by using the consistency of the poses of their parts.

Two layers in a hierarchy of parts

two_layer_hierarchy

• A higher level visual entity is present if several lower level visual entities can agree on their predictions for its pose (inverse computer graphics!)

A crucial property of the pose vectors

• They allow spatial transformations to be modeled by linear operations.
  • This makes it easy to learn a hierarchy of visual entities.
  • It makes it easy to generalize across viewpoints.
• The invariant geometric properties of a shape are in the weights, not in the activities.
  • The activities are equivariant: As the pose of the object varies, the activities all vary.
  • The percept of an object changes as the viewpoint changes.

Evidence that our visual systems impose coordinate frames in order to represent shapes (after Irvin Rock)

• What country is this? Hint: Sarah Palin

• The square and the diamond are very different percepts that make different properties obvious.

Lecture 16c Bayesian optimization of neural network hyperparameters

Let machine learning figure out the hyper-parameters!

(Snoek, Larochelle & Adams, NIPS 2012)

• One of the commonest reasons for not using neural networks is that it requires a lot of skill to set hyper-parameters.
  • Number of layers
  • Number of units per layer
  • Type of unit
  • Weight penalty
  • Learning rate
  • Momentum etc. etc.
• Naive grid search: Make a list of alternative values for each hyperparameter and then try all possible combinations.
  • Can we do better than this?
• Sampling random combinations: This is much better if some hyperparameters have no effect.
  • Its a big waste to exactly repeat the settings of the other hyperparameters.

Machine learning to the rescue

• Instead of using random combinations of values for the hyper-parameters, why not look at the results so far?
  • Predict regions of the hyperparameter space that might give better results.
  • We need to predict how well a new combination will do and also model the uncertainty of that prediction.
• We assume that the amount of computation involved in evaluating one setting of the hyper-parameters is huge.
  • Much more than the work involved in building a model that predicts the result from knowing previous results with different settings of the hyper-parameters.

Gaussian Process models

• These models assume that similar inputs give similar outputs.
  • This is a very weak but very sensible prior for the effects of hyper-parameters.
• For each input dimension, they learn the appropriate scale for measuring similarity.
  • Is 200 similar to 300?
  • Look to see if they give similar results in the data so far.
• GP models do more than just predicting a single value.
  • They predict a Gaussian distribution of values.
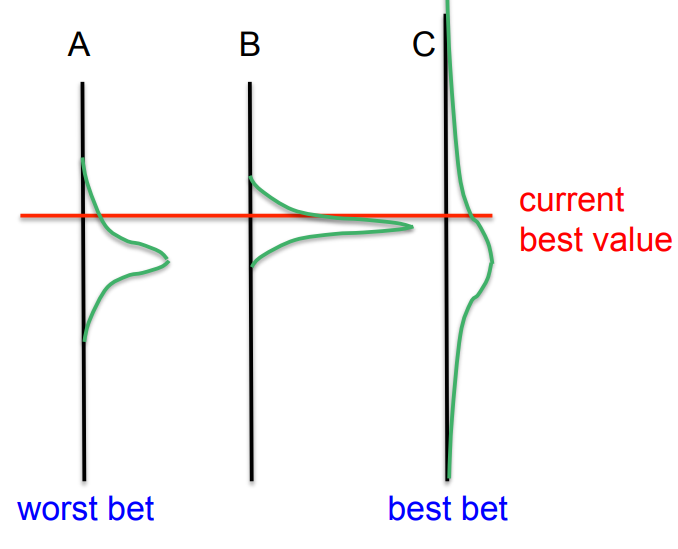
• For test cases that are close to several, consistent training cases the predictions are fairly sharp.
• For test cases far from any training cases, the predictions have high variance.

A sensible way to decide what to try

hedging.png

• Keep track of the best setting so far.
• After each experiment this might stay the same or it might improve if the latest result is the best.
• Pick a setting of the hyperparameters such that the expected improvement in our best setting is big.
  • don’t worry about the downside (hedge funds!)

How well does Bayesian optimization work?

• If you have the resources to run a lot of experiments, Bayesian optimization is much better than a person at finding good combinations of hyper-parameters.
  • This is not the kind of task we are good at.
  • We cannot keep in mind the results of 50 different experiments and see what they predict.
• It’s much less prone to doing a good job for the method we like and a bad job for the method we are comparing with.
  • People cannot help doing this. They try much harder for their own method because they know it ought to work better!

Lecture 16d The fog of progress

Why we cannot predict the long-term future

• Consider driving at night. The number of photons you receive from the tail-lights of the car in front falls off as \frac{1}{d^2}
• Now suppose there is fog.
  • For small distances its still \frac{1}{d^2}
  • But for big distances its \exp(-d) because fog absorbs a certain fraction of the photons per unit distance.
• So the car in front becomes completely invisible at a distance at which our short-range \frac{1}{d^2} model predicts it will be very visible.
  • This kills people.

The effect of exponential progress

• Over the short term, things change slowly and its easy to predict progress.
  • We can all make quite good guesses about what will be in the iPhone 6.
• But in the longer run our perception of the future hits a wall, just like fog.
• So the long term future of machine learning and neural nets is a total mystery.
  • But over the next five years, its highly probable that big, deep neural networks will do amazing things.