Temporal Abstraction in Reinforcement Learning with the Successor Representation

This paper review is an extended introduction to temporal abstraction using options. It covers lots of advanced concepts in reinforcement learning that were introduced in Doina’s Precup’s talk in the Coursera Specialization on Reinforcement Learning by Martha White and Adam White. The paper is a deep dive into the topic of options and the successor representation. It is a long paper with lots of advanced concepts and algorithms. The paper is a great resource for anyone interested in reinforcement learning and temporal abstraction.

Introduction

Ever since I saw (White 2022) the video lecture on subtasks by Martha White about learning tasks in parallel. However the video does not address the elephant in the room - how to discover the options.

White, Martha. 2022. “Developing Reinforcement Learning Agents That Learn Many Subtasks.” YouTube. https://www.youtube.com/watch?v=GmGL9cVfJG4&t=6s.

Figure 1: Talk at Waterloo.AI by Martha White on Developing Reinforcement Learning Agents that Learn Many Subtasks. She makes the case for the life long problem setting and discusses recent research on learning multiple tasks (options and GVFs) in parallel.

Figure 2: Talk at Cohere.AI by Marlos C. Machado on Representation-driven Option Discovery in Reinforcement Learning. He discusses the Representation-driven Option Discovery (ROD) cycle and how it can be used to discover options in reinforcement learning. The talk covers much of the material in the paper as well as some more recent follow up work.

———. 2024. “Representation-Driven Option Discovery in Reinforcement Learning.” YouTube. https://www.youtube.com/watch?v=m9gYmYEYuIs.

This is a hefty paper 70 pages with 8 algorithms many figures and citations from research spanning thirty years. It is filled to the brim with fascinating concepts that are developed by the authors but builds on lots of work by earlier researchers. It may seem to cover a niche topic but (c.f. Machado 2024, time 773) makes an eloquent argument that this paper deals with a fundamental question of where options come and if we put aside the jargon for a second we are trying to capture a form of intelingence that includes elements of generalization, planning, problem solving, learning at a level much closer what we are familiar with. And these familiar forms of mental abstractions much harder to consider in the context of Supervised or Unsupervised learning which lack the ineraction with the environment that is the hallmark of reinforcement learning.

I came about this paper by accident. I a quick summary before I realized how long it was and I put out my first pass, and I hope to flesh it including perhaps a bit of code.

I’ve been developing my own ideas regarding the creation and aggregation of options in reinforcement learning. My thinking to date has been different. I am exploring a Bayesian based tasks. I’ve considered creating shared semantics via emergent symbolic semantics and looking at a number of composability mechanisms for state, language and of options including using hierarchial bayesian models. While working on coding environments for this subjects a search led to this amazing paper!

In (reinforcement_2024?) Marlos C. Machado, has given a talk that explains many of the complex ideas within this paper. This talk is available on YouTube.

Marlos C. Machado is a good speaker and going over that paper and the video certainly helps to understand the challenges of temporal abstractions as well as the solutions that the paper proposes.

TL;DR

This paper posits that successor representations, which encode states based on the pattern of state visitation that follows them, can be seen as a natural substrate for the discovery and use of temporal abstraction like options if these are not known.

Options are a powerful form of temporal abstraction that allows agents to make predictions and to operate at different levels of abstraction within an environment in ways idiosyncratic of human approach to tackle many problems. One of the key questions has been how to discover good options. The paper presents a rather simple yet powerful answer to this.

Here is a lighthearted Deep Dive into the paper generated by notebooklm

Abstract

Reasoning at multiple levels of temporal abstraction is one of the key attributes of intelligence. In reinforcement learning, this is often modeled through temporally extended courses of actions called options. Options allow agents to make predictions and to operate at different levels of abstraction within an environment. Nevertheless, approaches based on the options framework often start with the assumption that a reasonable set of options is known beforehand. When this is not the case, there are no definitive answers for which options one should consider. In this paper, we argue that the successor representation, which encodes states based on the pattern of state visitation that follows them, can be seen as a natural substrate for the discovery and use of temporal abstractions. To support our claim, we take a big picture view of recent results, showing how the successor representation can be used to discover options that facilitate either temporally-extended exploration or planning. We cast these results as instantiations of a general framework for option discovery in which the agent’s representation is used to identify useful options, which are then used to further improve its representation. This results in a virtuous, never-ending, cycle in which both the representation and the options are constantly refined based on each other. Beyond option discovery itself, we also discuss how the successor representation allows us to augment a set of options into a combinatorially large counterpart without additional learning. This is achieved through the combination of previously learned options. Our empirical evaluation focuses on options discovered for temporally-extended exploration and on the use of the successor representation to combine them. Our results shed light on important design decisions involved in the definition of options and demonstrate the synergy of different methods based on the successor representation, such as eigenoptions and the option keyboard.

— (Machado et al. 2023)

The Review

Introduction

Figure 3: Doina Precup’s Talk at DeepHack.RL on Temporal abstraction in reinforcement learning covers both the intro and the background material on options.

In this section, the authors introduce the reinforcement learning problem and the options framework. Next they discuss the benefits of using options and highlight the option discovery problem. Next they present the successor representation (SR) as a representation learning method that is conducive to option discovery, summarizing its use cases and connecting it to neuroscience They go on to describe the paper’s focus on temporally-extended exploration and the use of eigenoptions and covering options. The finnish the introduction by highlight the paper’s evaluation methodology and the use of toy domains and navigation tasks for clarity and intuition.

In (Precup 2017) Doina precup gives a talk on temporal abstraction in reinforcement learning. This talk covers both the introduction and the background material on options and is on YouTube.

Precup, Doina. 2017. “DeepHack.RL: Temporal Abstraction in Reinforcement Learning.” YouTube. https://www.youtube.com/watch?v=GntIVgNKkCI.

Background

• Defines the reinforcement learning problem, covering Markov Decision Processes, policies, value functions, and common algorithms such as Q-learning.

• Introduces the options framework (Richard S. Sutton, Precup, and Singh 1999), (Precup and Sutton 2000), defining its components (initiation set, policy, termination condition), execution models, and potential benefits.

Sutton, Richard S., Doina Precup, and Satinder Singh. 1999. “Between MDPs and Semi-MDPs: A Framework for Temporal Abstraction in Reinforcement Learning.” Artificial Intelligence 112 (1): 181–211. https://doi.org/https://doi.org/10.1016/S0004-3702(99)00052-1.

Precup, Doina, and Richard S. Sutton. 2000. “Temporal Abstraction in Reinforcement Learning.” PhD thesis, University of Massachusetts Amherst.

An option \omega \in \Omega is a 3-tuple

\omega = <I_\omega , \pi_\omega , \beta_\omega > \qquad \tag{1}

• where
  • I_\omega ⊆ S the options’s initiation set,
  • \pi_\omega : \mathcal{S} \times \mathcal{A} \rightarrow [0, 1] the option’s policy, such that \sum_a \pi_\omega (·, a) = 1, and
  • \beta_\omega : \mathcal{S} \rightarrow [0, 1] the option’s termination condition ¹

¹ the probability that option ω will terminate at a given state.

A Framework for Option Discovery from Representation Learning

Figure 4: Representation-driven Option Discovery (ROD) cycle (Machado 2019). The option discovery algorithms discussed in this paper can be seen as instantiating this cycle. The incoming arrow to Collect samples depicts the start of the process. The arrow from Define option to Option set highlights the output generated by the ROD cycle. Note that other generated artifacts can also be used by the agent outside the ROD cycle, such as the learned representation.

Machado, Marlos C. 2019. “Efficient Exploration in Reinforcement Learning Through Time-Based Representations.” Revue De Geographie Alpine-Journal of Alpine Research. PhD thesis.

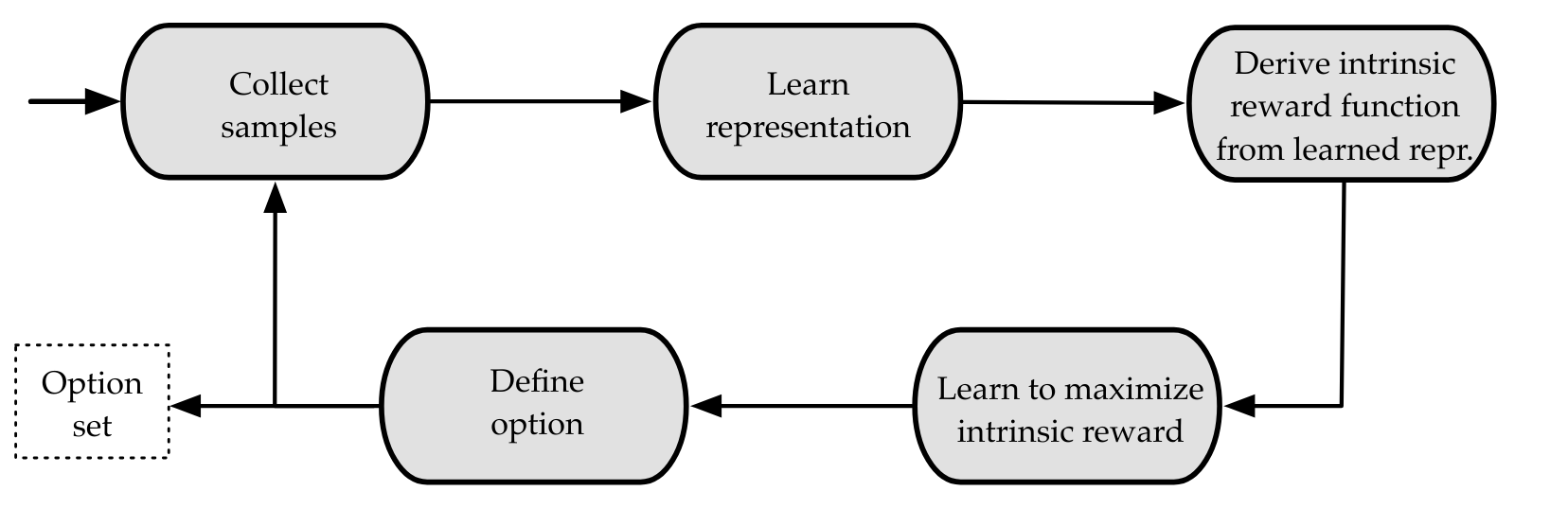
• Introduces a general framework for option discovery driven by representation learning, named the Representation-driven Option Discovery (ROD) cycle.

  • Collect samples
  • Learn a representation
  • Derive an intrinsic reward function from the representation
  • Learn to maximize intrinsic reward
  • Define option

• Presents a step-by-step explanation of the ROD cycle, outlining its iterative and constructivist nature, as depicted in the figure.

The Successor Representation

Figure 5: Example similar to Dayans 1993 of the SR, w.r.t. the uniform random policy, of state A (left). Consider a navigation task where the agent has access to its (x, y) coordinates. It is tempting to use some distance metric such as the Euclidean distance to define distance between states. However, if one considers the gray tiles to be walls, an agent in point A can reach point B much quicker than point C. The SR captures this distinction, ensuring that, in this representation, point A is closer to point B than it is to point C. The plots of the SR were generated using a discretization of the grid, where each tile is a state. Red represents larger values while blue represents smaller values (states that are temporally further away). Recall the SR of a state, in the tabular case, is an |S|-dimensional representation, thus allowing us to depict it as a heatmap over the state space.

• Presents the successor representation (SR) as a method to extract representations from observations.

• In (Machado et al. 2023, sec. 4.1) Defines the SR in the tabular setting, explaining its ability to capture environment dynamics by encoding expected future state visitation, as shown in Equation 7 and the figure.

\Psi_{\pi}(s,s') = \mathbb{E}_{\pi,p} \sum_{t=0}^\infty γ^t \mathbb{1}_{\{S_t=s'}\} | {S_0 = s } \qquad \tag{2}

Figure 6: First three PVFs in the (a) four-room domain. Gray squares represent walls and white squares represent accessible states. Four actions are available: up, down, right, and left. The transitions are deterministic and the agent is not allowed to move into a wall. (b-d) These plots depict the first, second, and third eigenvectors associated with each state. The axes are rotated for clarity. The bottom left corner of the four-room domain is the state closer to the reade

• Discusses the estimation of the SR with temporal-difference learning, its connection to general value functions ², and its relationship to the transition probability matrix Equation 9.

² “the SR can be estimated from samples with temporal-difference learning methods (Richard S. Sutton 1988), where the reward function is replaced by the state occupancy”

Sutton, Richard S. 1988. “Learning to Predict by the Methods of Temporal Differences.” Machine Learning 3: 9–44.

\Psi(S_t,j) \leftarrow \hat{\Psi}(S_t, j) + \eta [\mathbb{1}_{\{S_t=j\}} + \gamma \hat{\Psi}(S_{t+1}, j) − \hat{\Psi}(S_t, j)] \tag{3}

\Psi_\pi = \sum_{t=0}^\infty (\gamma P_\pi)^t = (I-\gamma P_\pi)^{-1}\qquad \tag{4}

• Introduces successor features (SFs) as a generalization of the SR to the function approximation setting, extending the definition of the SR to arbitrary features, as shown in Equation 11.

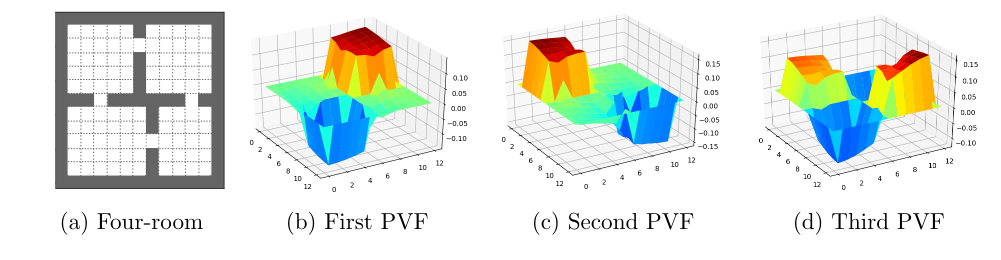
• Highlights the relationship between the SR and PVFs.

Temporally-Extended Exploration

• (Machado et al. 2023, sec. 5) discusses temporally-extended exploration with options and its potential to enhance exploration in RL.

• (Machado et al. 2023, sec. 5.1) introduces eigenoptions, which are options defined by the eigenvectors of the SR. > “Eigenoptions are options defined by the eigenvectors of the SR.2 Each eigenvector assigns an intrinsic reward to every state in the environment.”

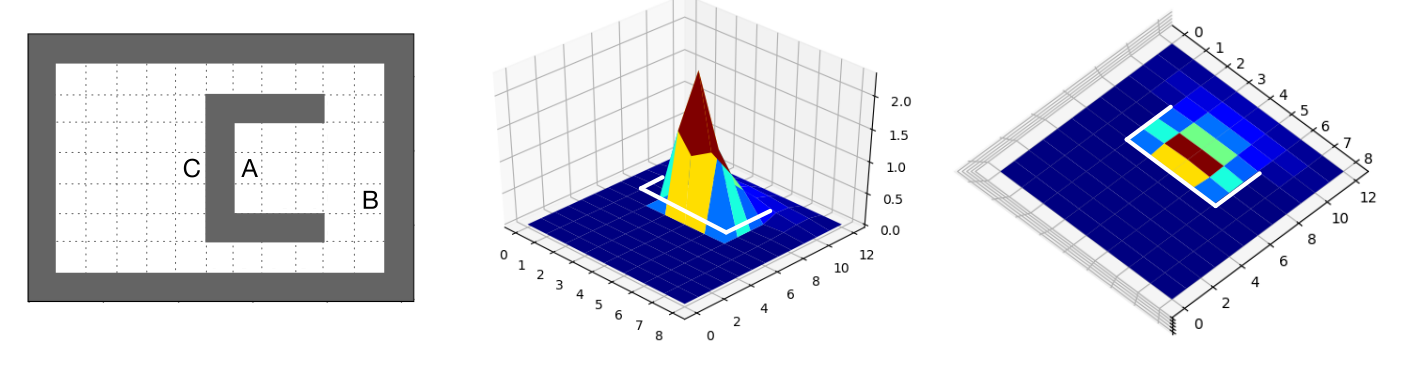
  • Explains the concept of eigenoptions using the four-room domain as an example (Figure 5).

  • Describes how to learn eigenoptions’ policies using an intrinsic reward function derived from the eigenvectors of the SR.

  • Defines the initiation set and termination condition of eigenoptions, as shown in Equation 16.

  • Presents Theorem 1, which guarantees the existence of at least one terminal state for each eigenoption.

• Introduces covering options, which are point options defined by the bottom eigenvector of the graph Laplacian and aim to minimize the environment’s cover time.

  • Explains the concept of covering options using the four-room domain (Figure 7).
  • Describes how to learn covering options’ policies using a simplified intrinsic reward function.
  • Defines the initiation set and termination condition of covering options.
  • Highlights the iterative nature of covering option discovery, where options are added one by one at each iteration.

Evaluation of Temporally-Extended Exploration with Options

• (Machado et al. 2023, sec. 6)Evaluates eigenoptions and covering options in the context of temporally-extended exploration.

• Uses the diffusion time, a task-agnostic metric, to quantify exploration effectiveness by measuring the expected number of decisions required to navigate between states.

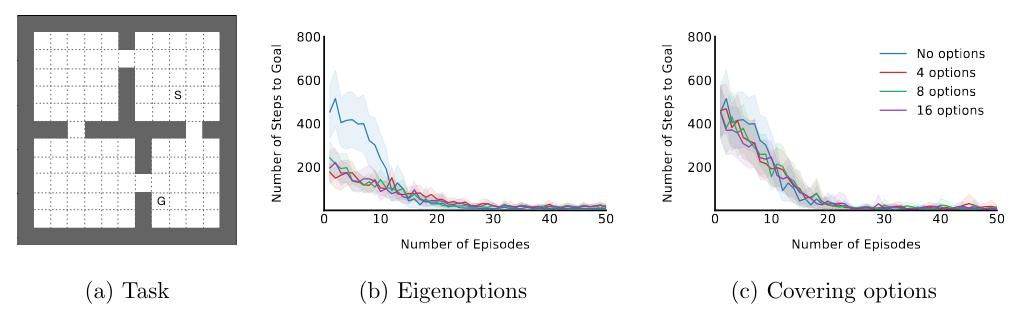
• Presents results comparing eigenoptions and covering options:

  • Shows that both approaches can reduce diffusion time in the four-room domain when computed in closed form (Figure 8).
  • Discusses the impact of different initiation set sizes, highlighting the trade-off between avoiding sink states and ensuring option availability.

• Investigates the effectiveness of eigenoptions and covering options in an online setting:

  • Demonstrates the robustness of eigenoptions to online SR estimation (Figure 11).
  • Reveals the challenges of using covering options online, particularly due to their restrictive initiation set and reliance on a single eigenvector (Figure 12).

• Explores the impact of using options on reward maximization in a fixed task:

  • Shows that eigenoptions can accelerate reward accumulation when used for temporally-extended exploration in Q-learning (Figure 9).
  • Observes that covering options do not consistently improve reward maximization in this setting, likely due to their sparse initiation set.

Figure 7: figure 9

Iterative Option Discovery with the ROD Cycle

• (Machado et al. 2023, sec. 7) introduces Covering Eigenoptions (CEO), a new algorithm that performs multiple iterations of the ROD cycle for option discovery.

• Describes the steps of CEO, emphasizing its use of eigenoptions and online SR estimation, as outlined in Algorithm 2.

• Demonstrates the benefits of multiple ROD cycle iterations with CEO, showing a significant reduction in the number of steps needed to visit all states in the four-room domain (Figure 14).

• Illustrates the behavior of CEO over multiple iterations, highlighting its ability to progressively discover more complex options (Figure 14).

• Combining Options with the Option Keyboard

• Discusses the option keyboard as a way to combine existing options to create new options without additional learning, potentially expanding the agent’s behavioral repertoire.

• Introduces Generalized Policy Evaluation (GPE) and Generalized Policy Improvement (GPI), generalizations of standard policy evaluation and improvement.

• Explains how to use GPE and GPI to synthesize options from linear combinations of rewards induced by eigenvectors of the SR, as outlined in Algorithm 3.

• Combining Eigenoptions with the Option Keyboard

• Demonstrates the synergy of eigenoptions and the option keyboard.

• Presents a qualitative analysis of options generated by combining eigenoptions with the option keyboard (Figures 16 and 17).

• Shows that the option keyboard leads to a combinatorial explosion of new options, as evidenced by the number of unique options generated (Figure 18).

• Demonstrates the diversity of options generated by the option keyboard through heatmaps showing the frequency of termination in different states (Figures 19 and 20).

• Presents a quantitative analysis of the diffusion time induced by eigenoptions combined with the option keyboard, highlighting the improvement in exploration effectiveness (Figures 21 and 22).

Machado, Marlos C., Andre Barreto, Doina Precup, and Michael Bowling. 2023. “Temporal Abstraction in Reinforcement Learning with the Successor Representation.” Journal of Machine Learning Research 24 (80): 1–69. http://jmlr.org/papers/v24/21-1213.html.

Related Work

• Discusses option discovery methods for planning and bottleneck options, including those based on spectral clustering and normalized cuts.
• Mentions other option discovery methods for temporally-extended exploration, such as diffusion options.
• Outlines extensions of the SR and option discovery methods to function approximation, including linear and non-linear function approximation techniques.
• Discusses the connection of the SR to other reinforcement learning concepts, such as proto-value functions, slow-feature analysis, and dual representations.
• Highlights the relationship of the SR to neuroscience, including its potential to model hippocampal place fields and grid cell activations.
• Mentions the SR’s application to explaining human behavior and decision-making.

Conclusion

• Highlights the potential of using the SR as the main substrate for temporal abstraction, pointing out promising directions for future work.
• Emphasizes the importance of iterative option discovery and its role in building intelligent agents capable of continual learning and complex skill acquisition.

Here are the successor representations algorithms from the paper:

Figure 8: successor representations algorithms

Next is the covering eigenoptions algorithm:

Figure 9: Covering Eigenoptions algorithm

Study guide for the paper

1. What is an option in reinforcement learning?

We actually took the definition from the paper. But here is another from the video. This is perhaps a more elegant definition. It comes from []

In reinforcement learning, an option is a temporally extended course of actions that allows an agent to operate at different levels of abstraction within an environment. Options are a form of temporal abstraction that enables agents to make predictions and execute actions over extended time horizons, providing a way to structure and organize the agent’s behavior. v_{\pi,\beta}^{c,z}(s) = \mathbb{E}_{\pi,\beta} \left[ \sum_{j=1}^K c(S_j) + \gamma^{K-1} z(S_k) | S_0 = s \right] \qquad \text{for all } s \in S

• where
  • v_{\pi,\beta}^{c,z}(s) is the value function of the option,
  • \pi is the policy,
  • \beta is the termination condition,
  • c is the extrinsic reward function, z is the intrinsic reward function,
  • S_j is the state at time j,
  • K is the duration of the option, and
  • \gamma is the discount factor.

1. How can options be used ?

• For planning: you can use eigenvectors of the SR to identify bottleneck, states that are difficult to reach under a random walk, and then use options to guide the agent to those states. c.f. (Solway et al. 2014)
• For exploration: you can use eigenoptions to encourage exploration by driving the agent toward states that are difficult to reach under a random walk.

Solway, Alec, Carlos Diuk, N. Córdova, Debbie M. Yee, A. Barto, Y. Niv, and M. Botvinick. 2014. “Optimal Behavioral Hierarchy.” PLoS Computational Biology 10.

1. Explain the successor representation

The successor representation (SR) is a method in reinforcement learning that represents states based on their expected future visits under a given policy. It captures the environment’s dynamics by encoding how likely an agent is to visit each state in the future, starting from a particular state.

• The SR is denoted as Ψ_π, where π represents the agent’s policy.
• It can be estimated online using temporal difference learning and generalized to function approximation using successor features.

The SR allows for Generalized Policy Evaluation (GPE): once the SR is learned, an agent can immediately evaluate its performance under any reward function that can be expressed as a linear combination of the features used to define the SR.

The SR offers a powerful tool for discovering and using temporal abstractions in reinforcement learning, enabling the development of more intelligent and efficient agents. It is used in option discovery methods like eigenoptions and covering options, providing a natural framework for identifying and leveraging temporally extended courses of actions.

Here is a breakdown of the mathematical definition of the SR:

Ψ_\pi (s, s') = \mathbb{E}_{π,p} [\sum^\infty_{t=0} γ^t\mathbb{1}_{S_t = s'} | S_0 = s ] \qquad \tag{5}

• Where:
  • s, s' are states in the environment.
  • \gamma is the discount factor, determining the weight of future rewards.
  • The expectation (E) is taken over the policy \pi and the transition probability kernel p.
  • \mathbb{1}_{S_t = s'} is an indicator function that equals 1 if the agent is in state s’ at time t, and 0 otherwise.

This equation calculates the expected discounted number of times the agent will visit state s’ in the future, given that it starts in state s and follows policy π. The SR matrix stores these expected visitations for all state pairs.

2. Explain what is an eigenoption a covering option and the difference

Eigenoptions and covering options are two methods for option discovery in RL that use the successor representation (SR). Options represent temporally extended courses of actions.

Eigenoptions are options defined by the eigenvectors of the SR.

• Each eigenvector of the SR assigns an intrinsic reward to every state in the environment.
• An eigenoption aims to reach the state with the highest (or lowest) value in the corresponding eigenvector.
• They encourage exploration by driving the agent toward states that are difficult to reach under a random walk.
• Eigenoptions have a broad initiation set, meaning they can be initiated from many states.
• They terminate when the agent reaches a state with a (locally) maximum value in the eigenvector, meaning the agent can’t accumulate more positive intrinsic reward.
• Eigenoptions tend to have different durations based on the eigenvalue they are derived from, allowing the agent to operate at different timescales.

Covering options are defined by the bottom eigenvector of the graph Laplacian, which is equivalent to the top eigenvector of the SR under certain conditions.

• They aim to minimize the environment’s expected cover time, which is the number of steps needed for a random walk to visit every state.
• Each covering option connects two specific states: one with the lowest value and one with the highest value in the corresponding eigenvector.
• They are discovered iteratively. After each option is discovered, the environment’s graph is updated, and the process repeats.
• Covering options have a restrictive initiation set, containing only the single state with the lowest value in the eigenvector.
• They terminate when they reach the state with the highest value in the eigenvector.

Here’s a table summarizing the key differences between eigenoptions and covering options:

Feature	Eigenoption	Covering Option
Definition	Based on any eigenvector of the SR	Based on the bottom eigenvector of the graph Laplacian (equivalent to the top eigenvector of the SR under certain conditions)
Goal	Reach states with high/low values in the corresponding eigenvector	Minimize environment’s cover time
Initiation Set	Broad (many states)	Restrictive (single state)
Termination Condition	Reaching a (local) maximum in the eigenvector	Reaching the state with the highest value in the eigenvector
Discovery Process	Can be discovered in parallel, in a single iteration	Discovered iteratively, one option at a time
Timescale	Different eigenoptions can have different durations	Generally have similar durations

Both eigenoptions and covering options can be effective for exploration, but they have different strengths and weaknesses. Eigenoptions can learn more diverse behaviors and capture different timescales, while covering options may be simpler to implement and can guarantee improvement in the environment’s cover time.

The paper

paper

Resources

There are a few blog posts that dive deeper into some of the concepts in the paper.

• The Representation-driven Option Discovery