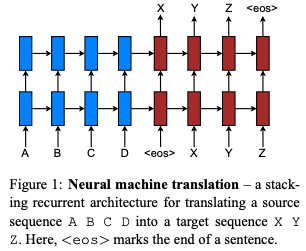
Dot-Product Attention
Dot-Product attention is the first of three attention mechanisms covered in the course and the simplest covered in this paper. Dot-Product Attention is a good fit, in an engineering sense, for a encoder-decoder architecture with tasks where the source source sequence is fully available at the start and the tasks is mapping or transformation the source sequence to an output sequence like in alignment, or translation.
The first assignment in the course using encoder decoder LSTM model with attention is so similar to the setup disused in this paper, I would not be surprised if it may well have inspired it.
This is a review of the paper in which scaled dot product attention was introduced in 2015 by Minh-Thang Luong, Hieu Pham, Christopher D. Manning in Effective Approaches to Attention-based Neural Machine Translation which is available at papers with code. In this paper they tried to take the attention mechanism being used in other tasks and to distill it to its essence and at the same time to also find a more general form.
| Global Attention | Local Attention |
|---|---|
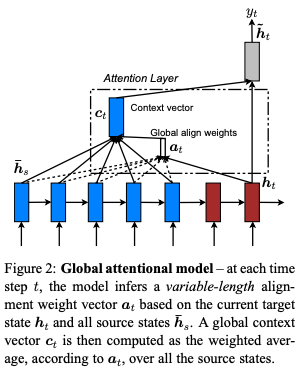 |
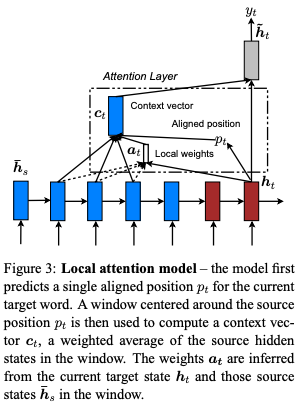 |
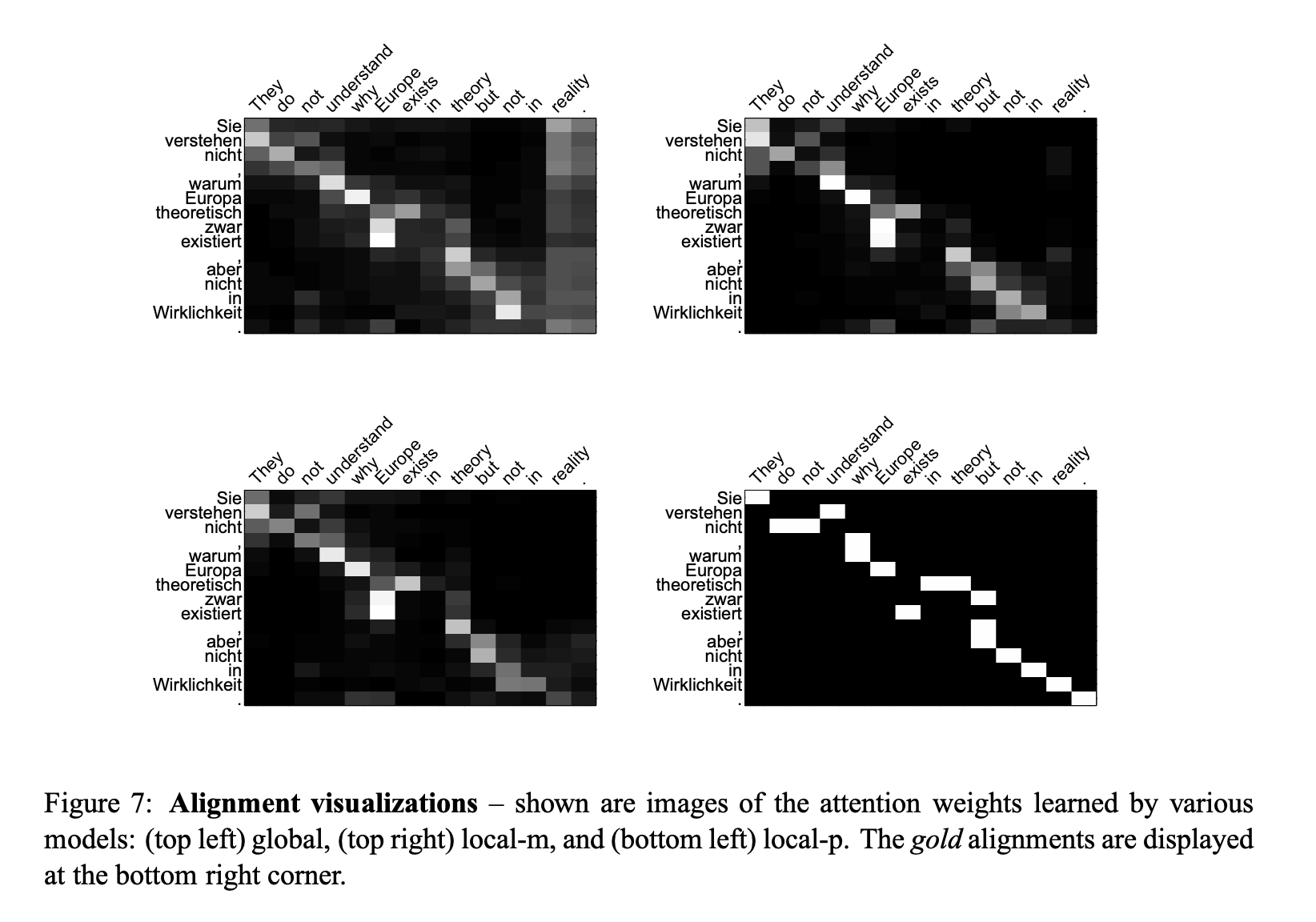
They also came up with a interesting way to visualize the alignment’s attention mechanism.
So to recap: Luong et all were focused on alignment problem in NMT. When they try to tackle it using attention as function of the content and a function of its location. They came up with a number of ways to distill and generalize the attention mechanism.
Attention was just another engineering technique to improve alignment and it had not yet taken center stage in the models, as it would in Attention Is All You Need (Vaswani et al, 2017).I find it useful to garner the concepts and intuition which inspired these researchers to adapt attention and how they come up with this form of attention.
The abstract begins with:
“An attentional mechanism has lately been used to improve neural machine translation (NMT) by selectively focusing on parts of the source sentence during translation.”
which was covered in last lesson. The abstract continues with:
“This paper examines two simple and effective classes of attentional mechanism: a global approach which always attends to all source words and a local one that only looks at a
subset of source words at a time.”
talks about
§2 Neural Machine Translation:
This section provides a summary of the the NMT task using 4 equations:
In particular they note that in the decoder the conditional probability of the target given the source is of the form:
log \space p(y \vert x) = \sum_{j=1}^m log \space p (y_j \vert y_{<j} , s)
Where x_i are the source sentence and y_i are the target sentence.
p (y_j \vert y{<j} , s) = softmax (g(h_j)) Here, h_j is the RNN hidden unit, abstractly computed as:
h_j = f(h_{j-1},s)
Our training objective is formulated as follows
J_t=\sum_{(x,y)\in D} -log \space p(x \vert y)
With D being our parallel training corpus.
§3 Overview of attention
Next they provide a recap of the attention mechanism to set their starting point:
Specifically, given the target hidden state h_t and the source-side context vector c_t, we employ a simple concatenation layer to combine the information from both vectors to produce an attentional hidden state as follows:
\bar{h}_t = tanh(W_c[c_t;h_t]) > The attentional vector \bar{h}_t is then fed through the softmax layer to produce the predictive distribution formulated as: p(y_t|y{<t}, x) = softmax(W_s\bar{h}_t)
§3.1 Global attention
This is defined in §3.1 of the paper as:
\begin{align} a_t(s) & = align(h_t,\bar{h}_s) \newline & = \frac{ e^{score(h_t,\bar{h}_s)} }{ \sum_{s'} e^{score(h_t,\bar{h}_s)} } \newline & = softmax(score(h_t,\bar{h}_s)) \end{align} where h_t and h_s are the target and source sequences and score() which is referred to as a content-based function as one of three alternative forms provided:
Dot product attention:
score(h_t,\bar{h}_s)=h_t^T\bar{h}_s
This form combines the source and target using a dot product. Geometrically this essentially a projection operation.
General attention:
score(h_t,\bar{h}_s)=h_t^TW_a\bar{h}_s
this form combines the source and target using a dot product after applying a learned attention weights to the source. Geometrically this is a projection of the target on a linear transformation of the source or scaled dot product attention as it is now known
Concatenative attention:
score(h_t,\bar{h}_s)=v_a^T tanh(W_a [h_t;\bar{h}_s])
This is a little puzzling v_a^T is not accounted for and seems to be a learned attention vector which is projected onto the linearly weighted combination of the hidden states of the encoder and decoder.
they also mention having considered using a location based function
location :
a_t = softmax(W_a h_t)
which is just a linear transform of the hidden target state h_t
§3.2 Local Attention
in §3.2 they consider a local attention mechanism. This is a resource saving modification of global attention using the simple concept of applying the mechanism within a fixed sized window.

We propose a local attentional mechanism that chooses to focus only on a small subset of the source positions per target word. This model takes inspiration from the tradeoff between the soft and hard attentional models proposed by Xu et al. (2015) to tackle the image caption generation task.
Our local attention mechanism selectively focuses on a small window of context and is differentiable. … In concrete details, the model first generates an aligned position p_t for each target word at time t. The context vector c_t
is then derived as a weighted average over the set of source hidden states within the window [p_t−D, p_t+D]; Where D is empirically selected.
The big idea here is to use a fixed window size for this step to conserve resources when translating paragraphs or documents - a laudable notion for times where LSTM gobbled up resources in proportion to the sequence length…
They also talk about monotonic alignment where p_t=t and predictive alignment
p_t=S\cdot sigmoid(v_p^Ttanh(W_ph_t))
a_t(s)=align(h_t,\bar{h}_s)e^{(-\frac{(s-p_t)^2}{s\sigma^2})}
with align() as defined above and
\sigma=\frac{D}{2}
The rest of the paper has details about the experiment and is of less interest
In §5.4 In alignment quality
some sample translations
the references

This is appendix A which shows the visualization of alignment weights.

Citation
@online{bochman2021,
author = {Bochman, Oren},
title = {Effective {Approaches} to {Attention-based} {NMT}},
date = {2021-03-21},
url = {https://orenbochman.github.io/posts/2021/2021-03-21-review-of-effective-approaches-to-attention-based-neural-machine-translation/2021-03-21-review-of-effective-approaches-to-attention-based-neural-machine-translation.html},
langid = {en}
}