Lecture 7c: A toy example of training an RNN
Clarification at 3:33: there are two input units. Do you understand what each of those two is used for?
The hidden units, in this example, as in most neural networks, are logistic. That’s why it’s somewhat reasonable to talk about binary states: those are the extreme states.
A good toy problem for a recurrent network
:::  :::
:::
- We can train a feedforward net to do binary addition, but there are obvious regularities that it cannot capture efficiently.
- We must decide in advance the maximum number of digits in each number.
- The processing applied to the beginning of a long number does not generalize to the end of the long number because it uses different weights.
- As a result, feedforward nets do not generalize well on the binary addition task.
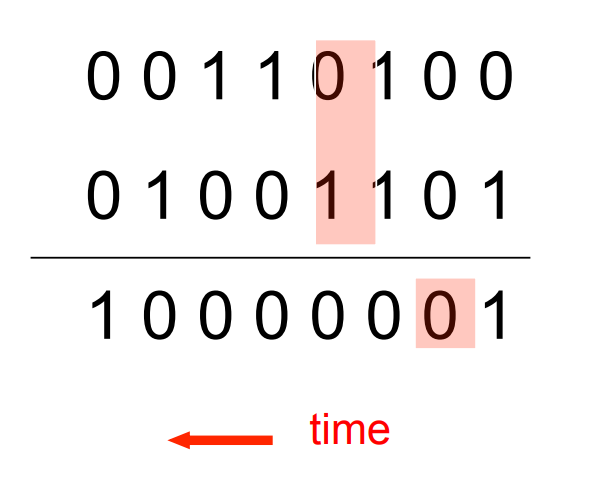
The algorithm for binary addition
This is a finite state automaton. It decides what transition to make by looking at the next column. It prints after making the transition. It moves from right to left over the two input numbers.
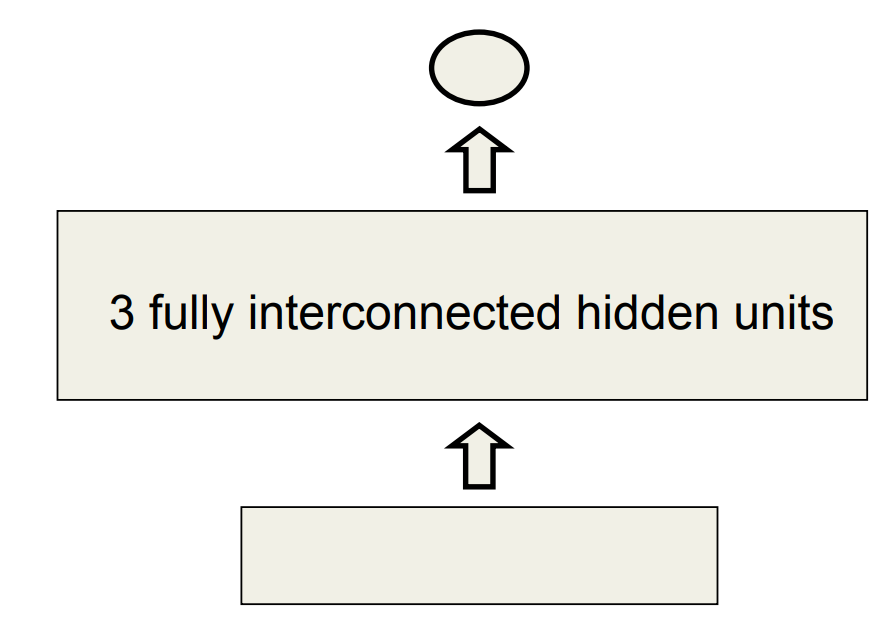
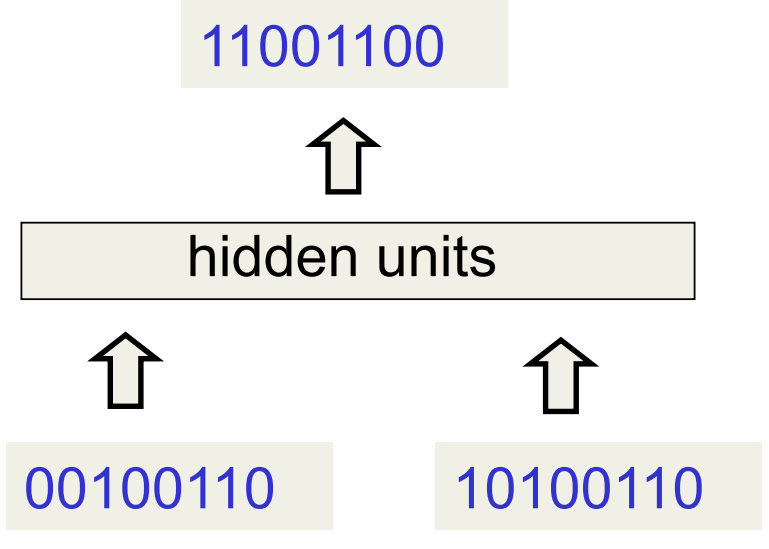
A recurrent net for binary addition
- The network has two input units and one output unit.
- It is given two input digits at each time step.
- The desired output at each time step is the output for the column that was provided as input two time steps ago.
- It takes one time step to update the hidden units based on the two input digits.
- It takes another time step for the hidden units to cause the output
The connectivity of the network
The 3 hidden units are fully interconnected in both directions. - This allows a hidden activity pattern at one time step to vote for the hidden activity pattern at the next time step. - The input units have feedforward connections that allow then to vote for the next hidden activity pattern.
What the network learns
- It learns four distinct patterns of activity for the 3 hidden units. These patterns correspond to the nodes in the finite state automaton.
- Do not confuse units in a neural network with nodes in a finite state automaton. Nodes are like activity vectors.
- The automaton is restricted to be in exactly one state at each time. The hidden units are restricted to have exactly one vector of activity at each time.
- A recurrent network can emulate a finite state automaton, but it is exponentially more powerful. With N hidden neurons it has 2^N possible binary activity vectors (but only N^2 weights)
- This is important when the input stream has two separate things going on at once.
- A finite state automaton needs to square its number of states.
- An RNN needs to double its number of units.
Reuse
Citation
@online{bochman2017,
author = {Bochman, Oren},
title = {Deep {Neural} {Networks} - {Notes} for {Lesson} 7c},
date = {2017-09-04},
url = {https://orenbochman.github.io/notes/dnn/dnn-07/l07c.html},
langid = {en}
}