Lecture 7a: Modeling sequences: A brief overview
This video talks about some advanced material that will make a lot more sense after you complete the course: it introduces some generative models for unsupervised learning (see video 1e), namely Linear Dynamical Systems and Hidden Markov Models. These are neural networks, but they’ve very different in nature from the deterministic feed forward networks that we’ve been studying so far. For now, don’t worry if those two models feel rather mysterious.
However, Recurrent Neural Networks are the next topic of the course, so make sure that you understand them.
Getting targets when modeling sequences
- When applying machine learning to sequences, we often want to turn an input sequence into an output sequence that lives in a different domain.
- E. g. turn a sequence of sound pressures into a sequence of word identities.
- When there is no separate target sequence, we can get a teaching signal by trying to predict the next term in the input sequence.
- The target output sequence is the input sequence with an advance of 1 step.
- This seems much more natural than trying to predict one pixel in an image from the other pixels, or one patch of an image from the rest of the image.
- For temporal sequences there is a natural order for the predictions.
- Predicting the next term in a sequence blurs the distinction between supervised and unsupervised learning.
- It uses methods designed for supervised learning, but it doesn’t require a separate teaching signal.
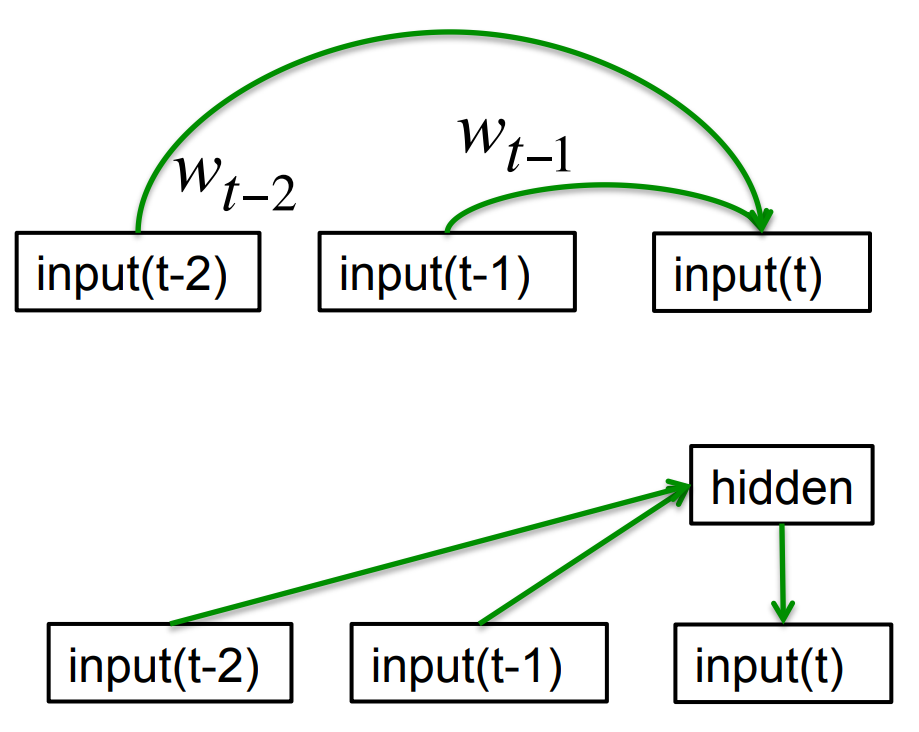
Memoryless models for sequences
- Autoregressive models Predict the next term in a sequence from a fixed number of previous terms using delay taps.
- Feed-forward neural nets These generalize autoregressive models by using one or more layers of non-linear hidden units. e.g. Bengio’s first language model.
Beyond memoryless models
- If we give our generative model some hidden state, and if we give this hidden state its own internal dynamics, we get a much more interesting kind of model.
- It can store information in its hidden state for a long time.
- If the dynamics is noisy and the way it generates outputs from its hidden state is noisy, we can never know its exact hidden state.
- The best we can do is to infer a probability distribution over the space of hidden state vectors.
- This inference is only tractable for two types of hidden state model.
- The next three slides are mainly intended for people who already know about these two types of hidden state model. They show how RNNs differ.
- Do not worry if you cannot follow the details.
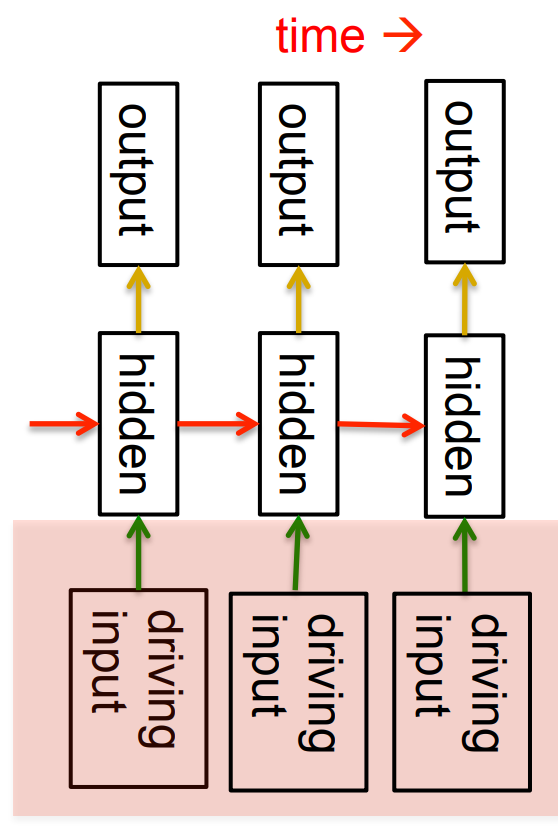
Linear Dynamical Systems (engineers love them!)
- These are generative models. They have a real valued hidden state that cannot be observed directly.
- The hidden state has linear dynamics with Gaussian noise and produces the observations using a linear model with Gaussian noise.
- There may also be driving inputs.
- To predict the next output (so that we can shoot down the missile) we need to infer the hidden state.
- A linearly transformed Gaussian is a Gaussian. So the distribution over the hidden.
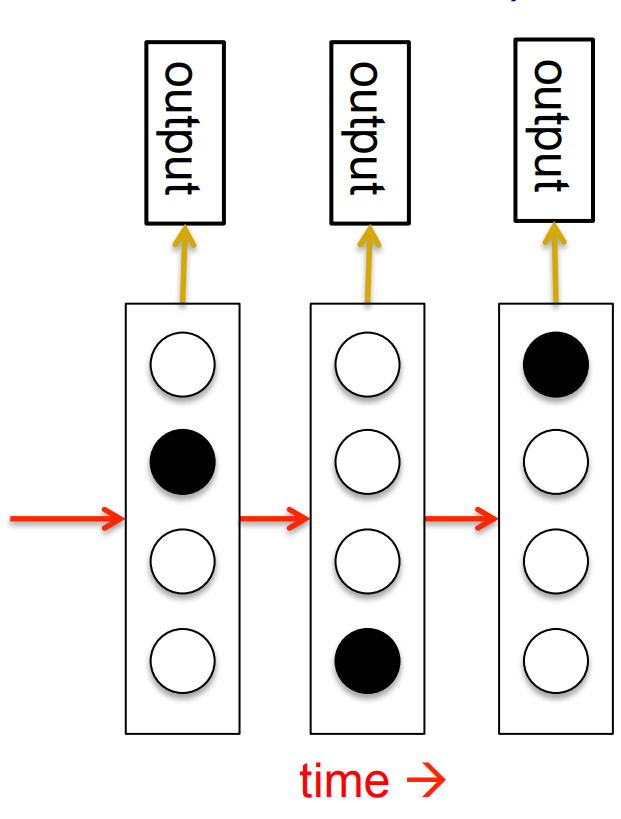
A fundamental limitation of HMMs
- Consider what happens when a hidden Markov model generates data.
- At each time step it must select one of its hidden states. So with N hidden states it can only remember log(N) bits about what it generated so far.
- Consider the information that the first half of an utterance contains about the second half:
- The syntax needs to fit (e.g. number and tense agreement).
- The semantics needs to fit. The intonation needs to fit.
- The accent, rate, volume, and vocal tract characteristics must all fit.
- All these aspects combined could be 100 bits of information that the first half of an utterance needs to convey to the second half. 2^100
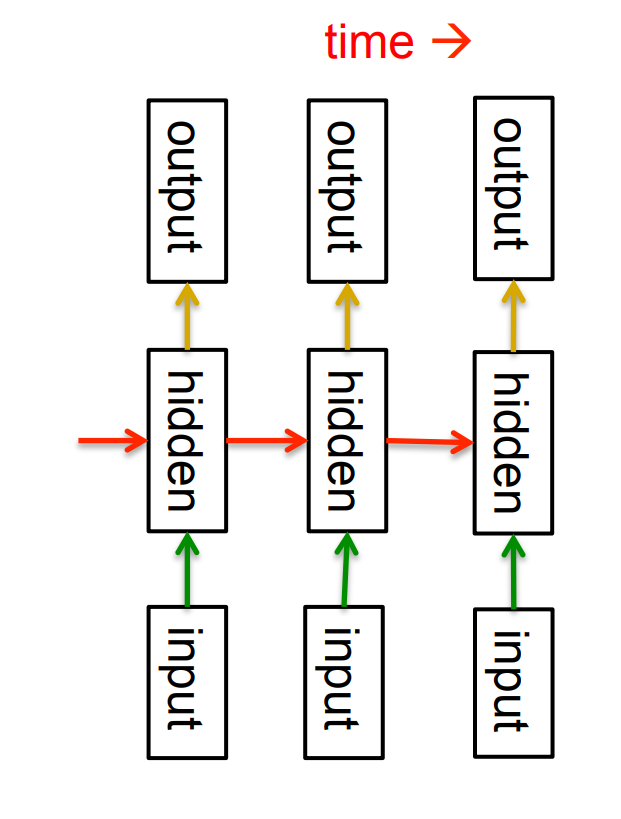
Recurrent neural networks
- RNNs are very powerful, because they combine two properties:
- Distributed hidden state that allows them to store a lot of information about the past efficiently.
- Non-linear dynamics that allows them to update their hidden state in complicated ways.
- With enough neurons and time, RNNs can compute anything that can be computed by your computer.
Do generative models need to be stochastic?
- Linear dynamical systems and hidden Markov models are stochastic models.
- But the posterior probability distribution over their hidden states given the observed data so far is a deterministic function of the data.
- Recurrent neural networks are deterministic.
- So think of the hidden state of an RNN as the equivalent of the deterministic probability distribution over hidden states in a linear dynamical system or hidden Markov model. ## Recurrent neural networks
- What kinds of behavior can RNNs exhibit?
- They can oscillate. Good for motor control?
- They can settle to point attractors. Good for retrieving memories?
- They can behave chaotically. Bad for information processing?
- RNNs could potentially learn to implement lots of small programs that each capture a nugget of knowledge and run in parallel, interacting to produce very complicated effects.
- But the computational power of RNNs makes them very hard to train.
- For many years we could not exploit the computational power of RNNs despite some heroic efforts (e.g. Tony Robinson’s speech recognizer).
Reuse
CC SA BY-NC-ND
Citation
BibTeX citation:
@online{bochman2017,
author = {Bochman, Oren},
title = {Deep {Neural} {Networks} - {Notes} for {Lesson} 7a},
date = {2017-09-02},
url = {https://orenbochman.github.io/notes/dnn/dnn-07/l07a.html},
langid = {en}
}
For attribution, please cite this work as:
Bochman, Oren. 2017. “Deep Neural Networks - Notes for Lesson
7a.” September 2, 2017. https://orenbochman.github.io/notes/dnn/dnn-07/l07a.html.