Deep Neural Networks - Notes for lecture 6a

{{< pdf lec6.pdf >}}

Lecture 6a: Overview of mini-batch gradient descent

Now we’re going to discuss numerical optimization: how best to adjust the weights and biases, using the gradient information from the backprop algorithm.

This video elaborates on the most standard neural net optimization algorithm (mini-batch gradient descent), which we’ve seen before.

We’re elaborating on some issues introduced in video 3e.

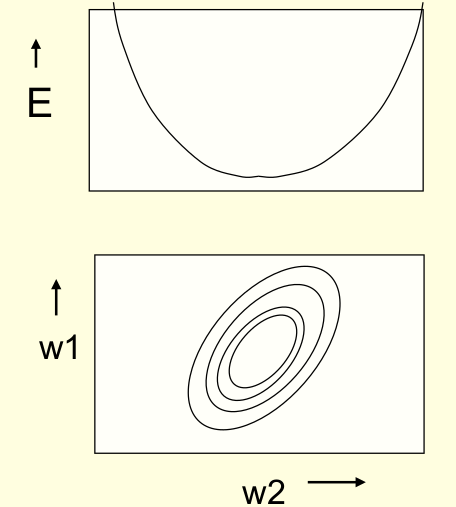
Reminder: The error surface for a linear neuron

error surface

• The error surface lies in a space with a horizontal axis for each weight and one vertical axis for the error.
  • For a linear neuron with a squared error, it is a quadratic bowl.
  • Vertical cross-sections are parabolas.
    • Horizontal cross-sections are ellipses.
• For multi-layer, non-linear nets the error surface is much more complicated.
  • But locally, a piece of a quadratic bowl is usually a very good approximation.

Convergence speed of full batch learning when the error surface is a quadratic bowl

error surface

• Going downhill reduces the error, but the direction of steepest descent does not point at the minimum unless the ellipse is a circle.
  • The gradient is big in the direction in which we only want to travel a small distance.
    
  • The gradient is small in the direction in which we want to travel a large distance.
• Even for non-linear multi-layer nets, the error surface is locally quadratic, so the same speed issues apply.

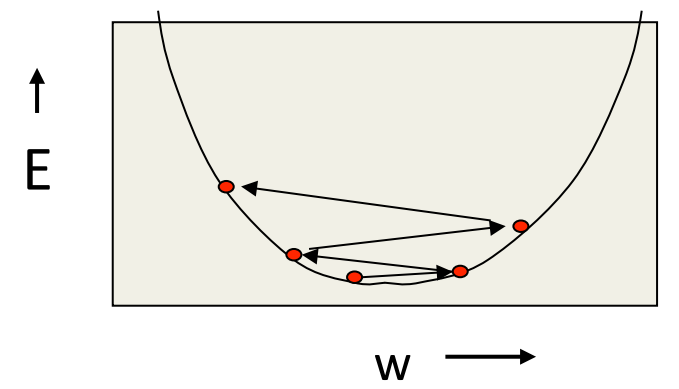
How the learning goes wrong

error surface

• If the learning rate is big, the weights slosh to and fro across the ravine.
  • If the learning rate is too big, this oscillation diverges.
• What we would like to achieve:
  • Move quickly in directions with small but consistent gradients.
  • Move slowly in directions with big but inconsistent gradients.

Stochastic gradient descent SGD

• If the dataset is highly redundant, the gradient on the first half is almost identical to the gradient on the second half.
  • So instead of computing the full gradient, update the weights using the gradient on the first half and then get a gradient for the new weights on the second half.
  • The extreme version of this approach updates weights after each case. Its called online.
• Mini-batches are usually better than online.
  • Less computation is used updating the weights.
  • Computing the gradient for many cases simultaneously uses matrix-matrix multiplies which are very efficient, especially on GPUs
• Mini-batches need to be balanced for classes

Two types of learning algorithm

• If we use the full gradient computed from all the training cases, there are many clever ways to speed up learning (e.g. non-linear conjugate gradient).
  • The optimization community has studied the general problem of optimizing smooth non-linear functions for many years.
    • Multilayer neural nets are not typical of the problems they study so their methods may need a lot of adaptation.
• For large neural networks with very large and highly redundant training sets, it is nearly always best to use mini-batch learning.
  • The mini-batches may need to be quite big when adapting fancy methods.
  • Big mini-batches are more computationally efficient.

A basic mini-batch gradient descent algorithm

• Guess an initial learning rate.
  • If the error keeps geang worse or oscillates wildly, reduce the learning rate.
  • If the error is falling fairly consistently but slowly, increase the learning rate.
    
• Write a simple program to automate this way of adjusting the learning rate.
• Towards the end of mini-batch learning it nearly always helps to turn down the learning rate.
  • This removes fluctuations in the final weights caused by the variations between minibatches.
    
• Turn down the learning rate when the error stops decreasing.
  • Use the error on a separate validation set