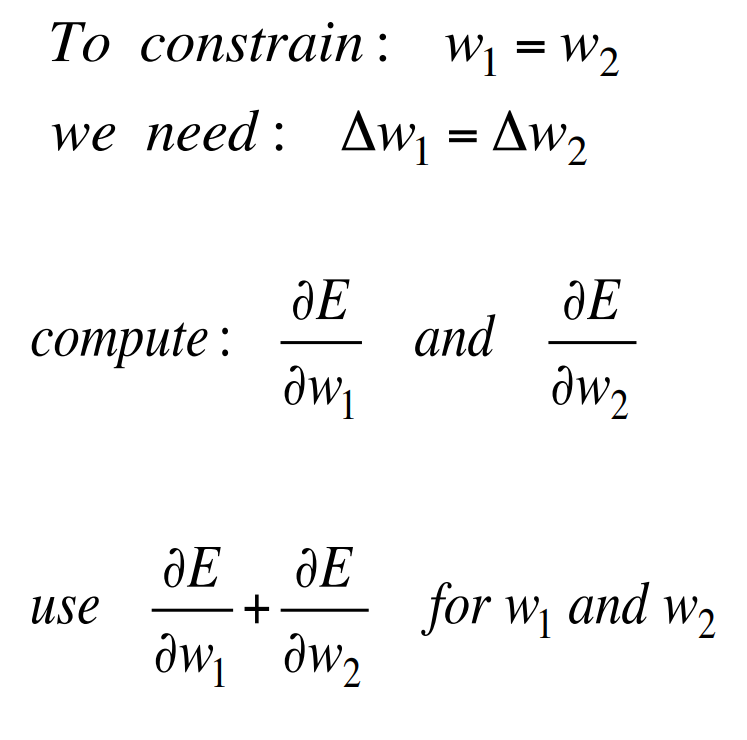Lecture 5c - Convolutional neural networks for hand-written digit recognition
Like many of the stories which we tell with the application of recognizing handwritten digits,
this one, too, is applicable to a great variety of vision tasks. It’s just that handwritten digit recognition is a standard example for neural networks - it used to be .
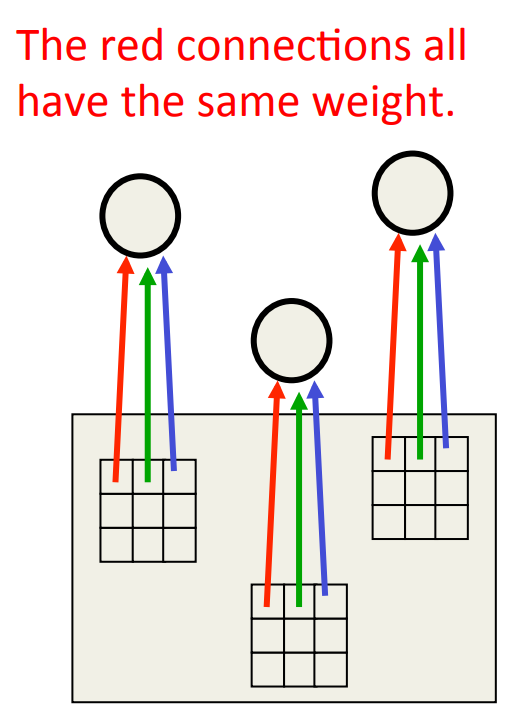
The replicated feature approach (currently the dominant approach for neural networks)
- Use many different copies of the same feature detector with different positions.
- Could also replicate across scale and orientation (tricky and expensive)
- Replication greatly reduces the number of free parameters to be learned.
- Use several different feature types, each with its own map of replicated detectors.
- Allows each patch of image to be represented in several ways.
Backpropagation with weight constraints
- It’s easy to modify the backpropagation algorithm to incorporate linear constraints between the weights.
- We compute the gradients as usual, and then modify the gradients so that they satisfy the constraints.
- So if the weights started off satisfying the constraints, they will continue to satisfy them.
What does replicating the feature detectors achieve?
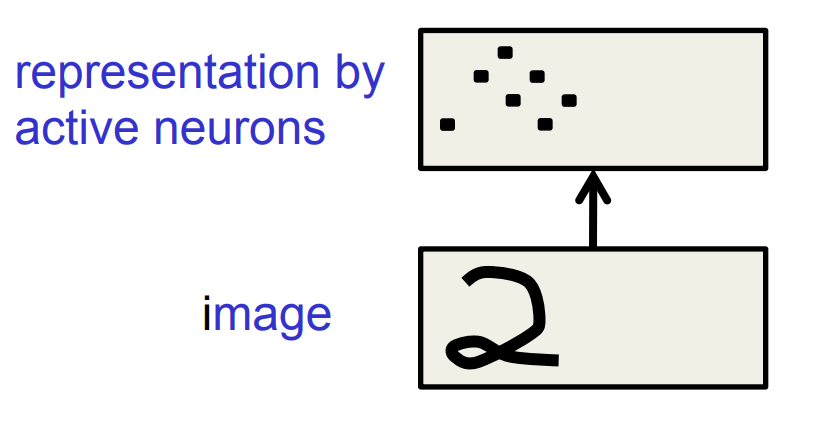
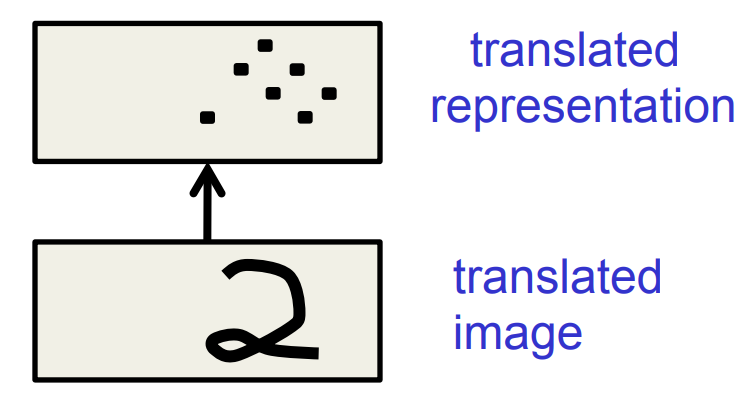
Equivariant activities: Replicated features do not make the neural activities invariant to translation. The activities are equivariant.
Invariant knowledge: If a feature is useful in some locations during training, detectors for that feature will be available in all locations during testing.
Pooling the outputs of replicated feature detectors
• Get a small amount of translational invariance at each level by averaging four neighboring replicated detectors to give a single output to the next level. – This reduces the number of inputs to the next layer of feature extraction, thus allowing us to have many more different feature maps. – Taking the maximum of the four works slightly better. • Problem: After several levels of pooling, we have lost information about the precise positions of things. – This makes it impossible to use the precise spatial relationships between high-level parts for recognition
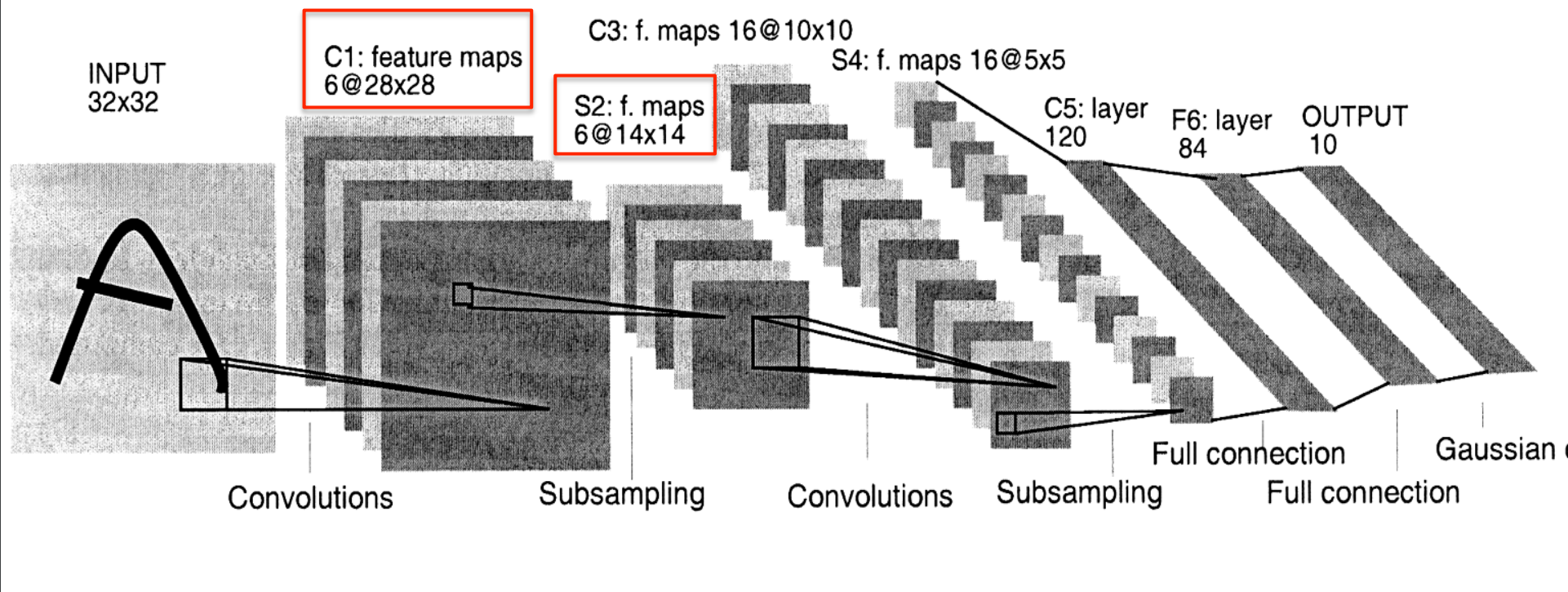
Le Net
- Yann LeCun and his collaborators developed a really good recognizer for handwriHen digits by using backpropagation in a feedforward net with:
- Many hidden layers
- Many maps of replicated units in each layer.
- Pooling of the outputs of nearby replicated units.
- A wide net that can cope with several characters at once even if they overlap.
- A clever way of training a complete system, not just a recognizer.
- This net was used for reading ~10% of the checks in North America.
- Look the impressive demos of LENET at demos
The architecture of LeNet5
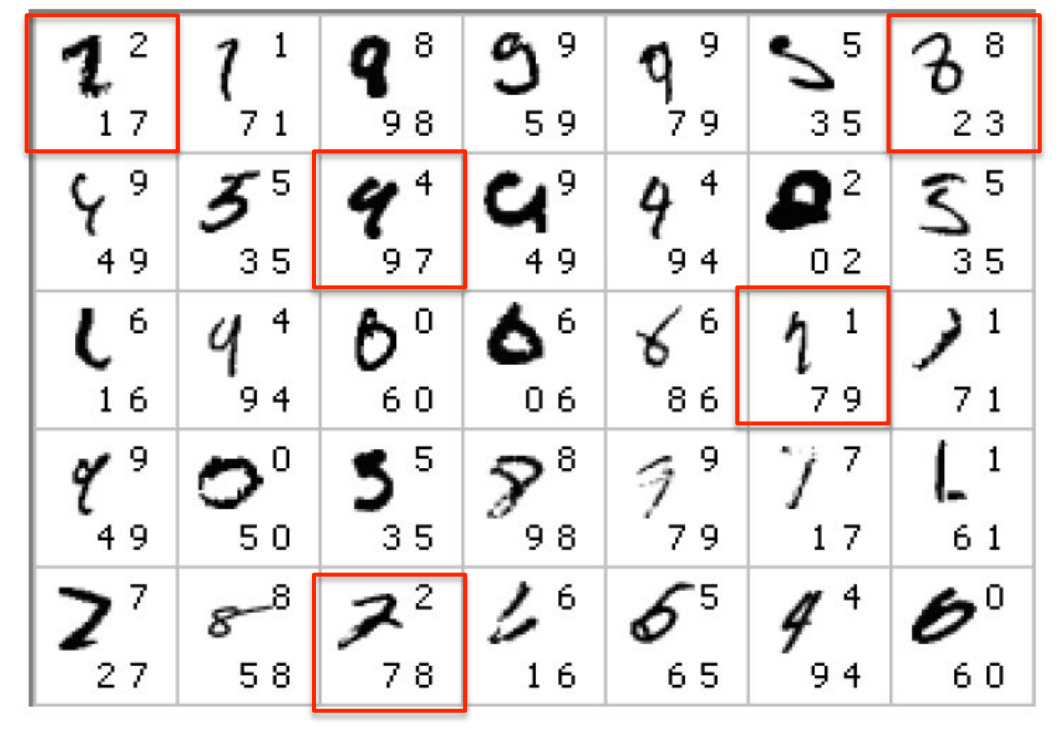
The 82 errors made by LeNet5
Notice that most of the errors are cases that people find quite easy.
The human error rate is probably 20 to 30 errors but nobody has had the patience to measure it.
Priors and Prejudice
- We can put our prior knowledge about the task into the network by designing appropriate:
- Connectivity.
- Weight constraints.
- Neuron activation functions
- This is less intrusive than handdesigning the features.
- But it still prejudices the network towards the particular way of solving the problem that we had in mind.
- Alternatively, we can use our prior knowledge to create a whole lot more training data.
- This may require a lot of work (Hofman&Tresp, 1993)
- It may make learning take much longer.
- It allows optimization to discover clever ways of using the multi-layer network that we did not think of.
- And we may never fully understand how it does it.
The brute force approach
- LeNet uses knowledge about the invariances to design:
- the local connectivity
- the weight-sharing
- the pooling.
- This achieves about 80 errors.
- This can be reduced to about 40 errors by using many different transformations of the input and other tricks (Ranzato 2008)
- Ciresan et. al. (2010) inject knowledge of invariances by creating a huge amount of carefully designed extra training data:
- For each training image, they produce many new training examples by applying many different transformations.
- They can then train a large, deep, dumb net on a GPU without much overfitting.
- They achieve about 35 errors.
The errors made by the Ciresan et. al. net
The top printed digit is the right answer. The bottom two printed digits are the network’s best two guesses.
The right answer is almost always in the top 2 guesses.
With model averaging they can now get about 25 errors.
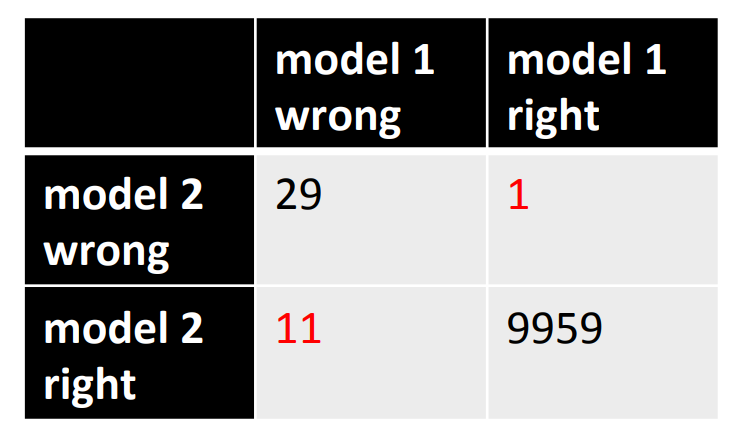
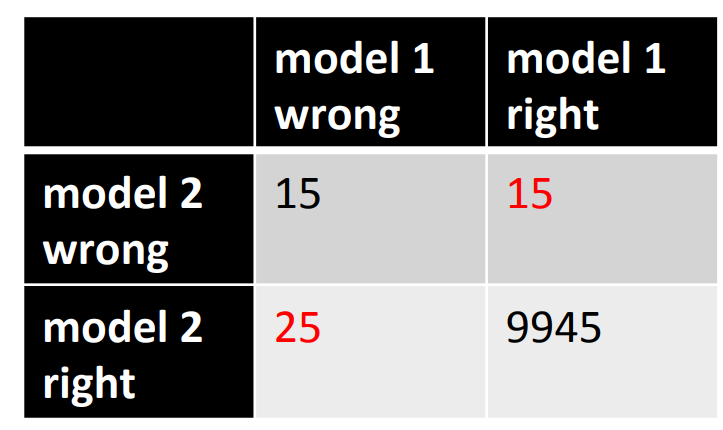
How to detect a significant drop in the error rate
- Is 30 errors in 10,000 test cases significantly beHer than 40 errors?
- It all depends on the particular errors!
- The McNemar test uses the particular errors and can be much more powerful than a test that just uses the number of errors.
Reuse
Citation
@online{bochman2017,
author = {Bochman, Oren},
title = {Deep {Neural} {Networks} - {Notes} for Lecture 5c},
date = {2017-08-20},
url = {https://orenbochman.github.io/notes/dnn/dnn-05/l05c.html},
langid = {en}
}