Deep Neural Networks - Notes for lecture 4e

Lecture 4e: Ways to deal with the large number of possible outputs

When softmax is very big it becomes hard to train and store.

1. A serial architecture, based on trying candidate next words, using feature vectors (like in the family example). This means fewer parameters, but still a lot of work.
2. Using a binary tree.
3. Collobert & Weston’s search for good feature vectors for words, without trying to predict the next word in a sentence.

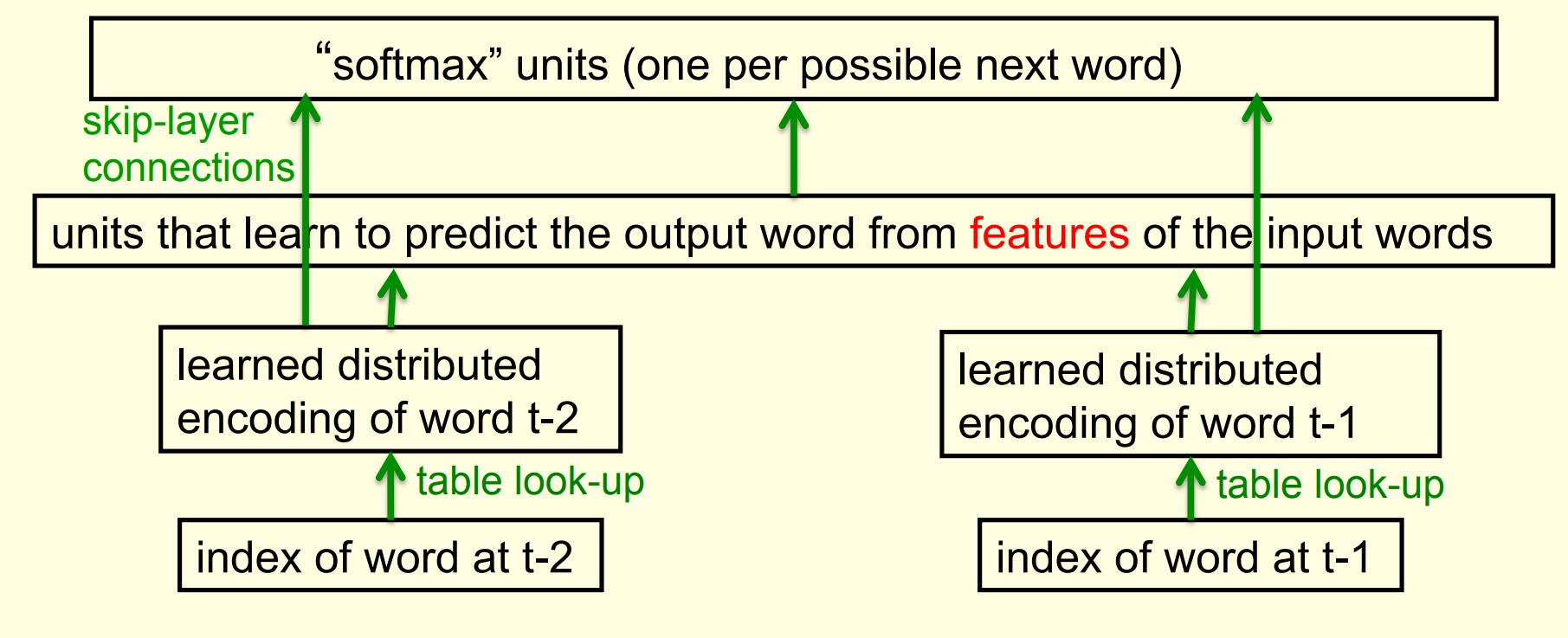
Bengio’s neural net for predicting the next word

A serial architecture

• Surprise this uses the same architecture

A serial architecture

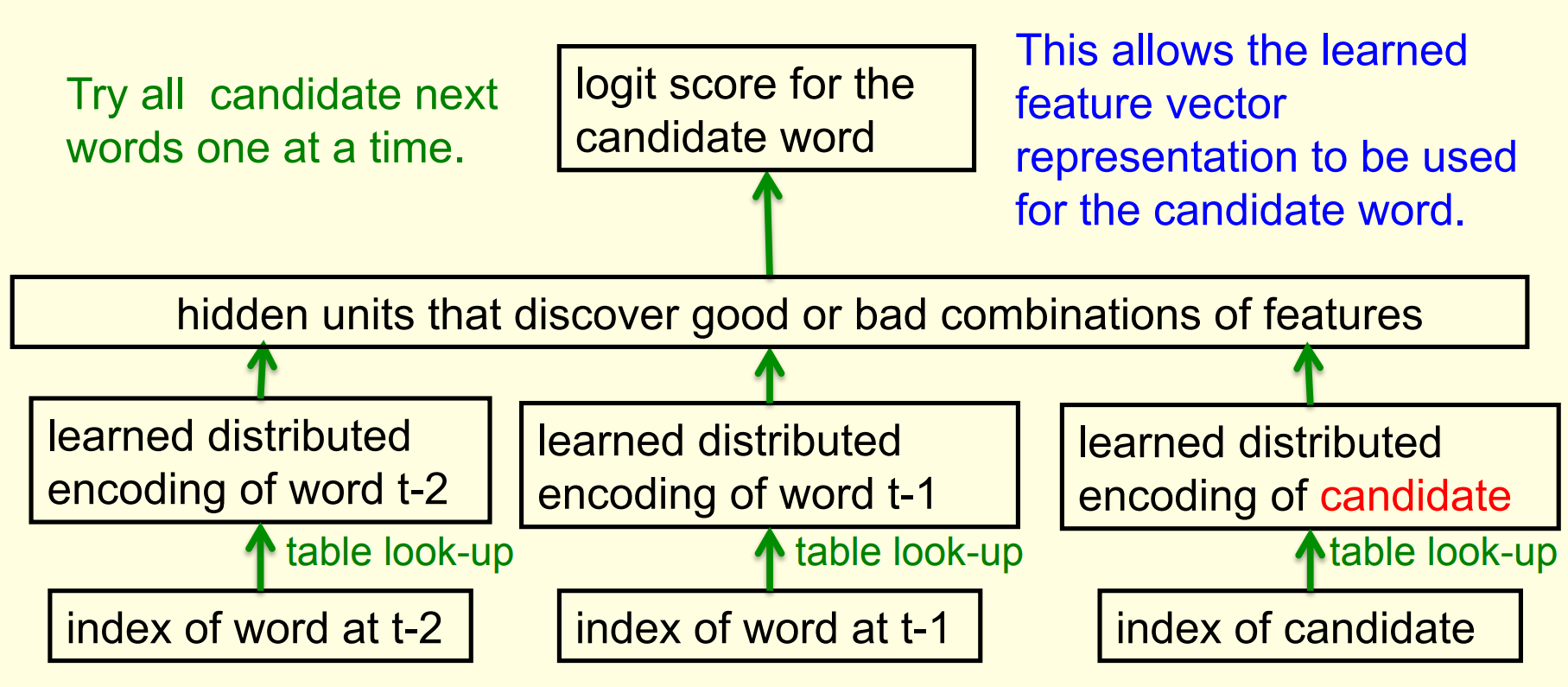
A serial architecture

• No Surprise this to uses basicaly the same architecture - only we are looking back.

Learning in the serial architecture

• After computing the logit score for each candidate word, use all of the logits in a softmax to get word probabilities.
• The difference between the word probabilities and their target probabilities gives cross-entropy error derivatives.
  • The derivatives try to raise the score of the correct candidate and lower the scores of its high-scoring rivals.
• We can save a lot of time if we only use a small set of candidates suggested by some other kind of predictor.
  • For example, we could use the neural net to revise the probabilities of the words that the trigram model thinks are likely.

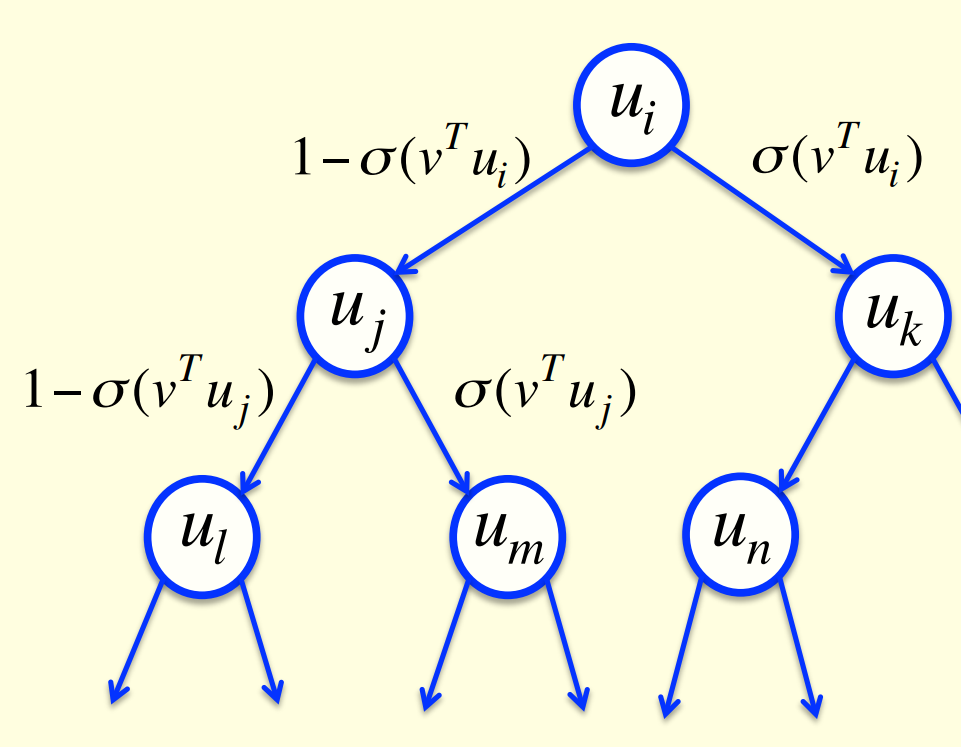
Learning to predict the next word by predicting a path through a tree

In Mnih, Yuecheng, and Hinton (2009) the authors show how to improve a state-of-the-art neural network language model that converts the previous “context” words into feature vectors and combines these feature vectors linearly to predict the feature vector of the next word.

Significant improvements in predictive accuracy are achieved by using a non-linear subnetwork to modulate the effects of the context words or to produce a non-linear correction term when predicting the feature vector.

Softmax as a tree

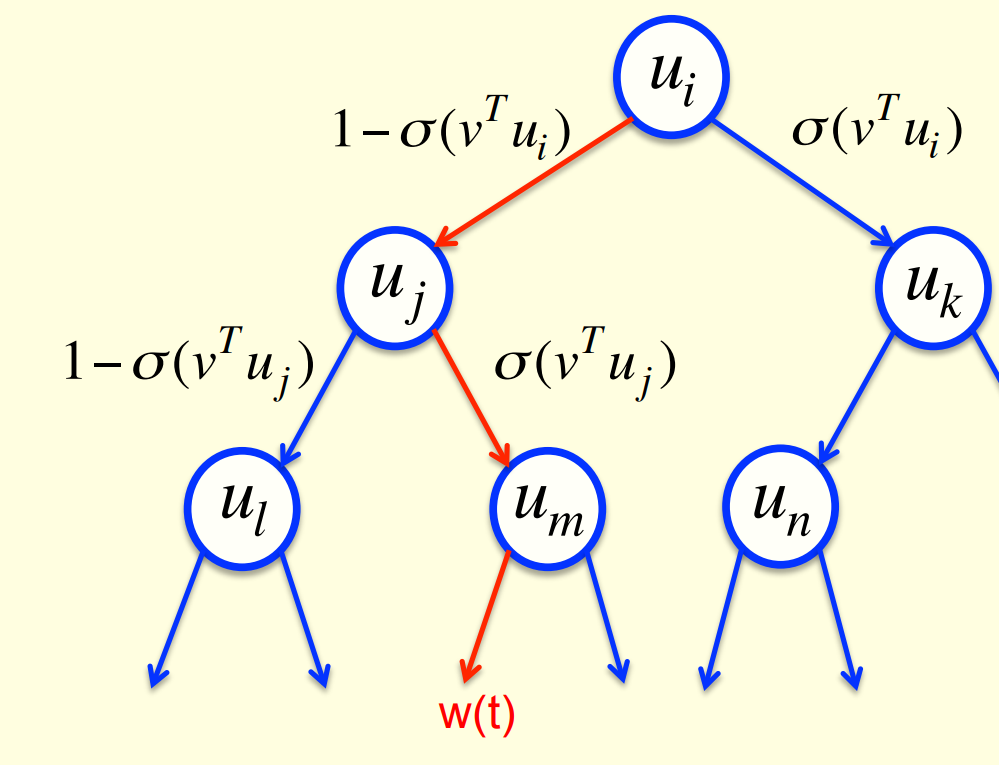
• Arrange all the words in a binary tree with words as the leaves.
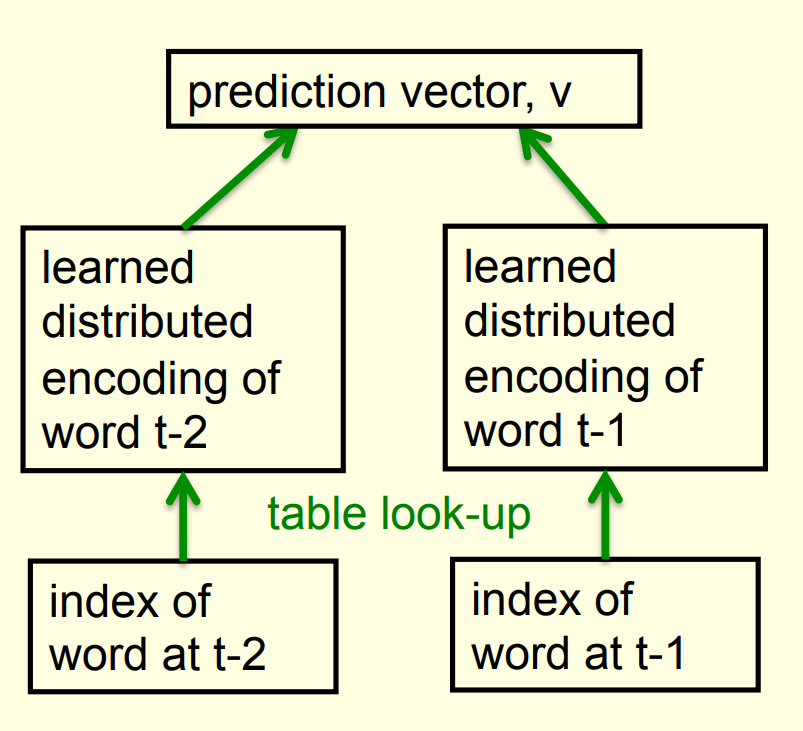
• Use the previous context to generate a prediction vector, v.
  • Compare v with a learned vector, u, at each node of the tree.
  • Apply the logistic function to the scalar product of u and v to predict the probabilities of taking the two branches of the tree.

A picture of the learning

A convenient decomposition

• Maximizing the log probability of picking the target word is equivalent to maximizing the sum of the log probabilities of taking all the branches on the path that leads to the target word.
  • So during learning, we only need to consider the nodes on the correct path. This is an exponential win: log(N) instead of N.
  • For each of these nodes, we know the correct branch and we know the current probability of taking it so we can get derivatives for learning both the prediction vector v and that node vector u.
• Unfortunately, it is still slow at test time.

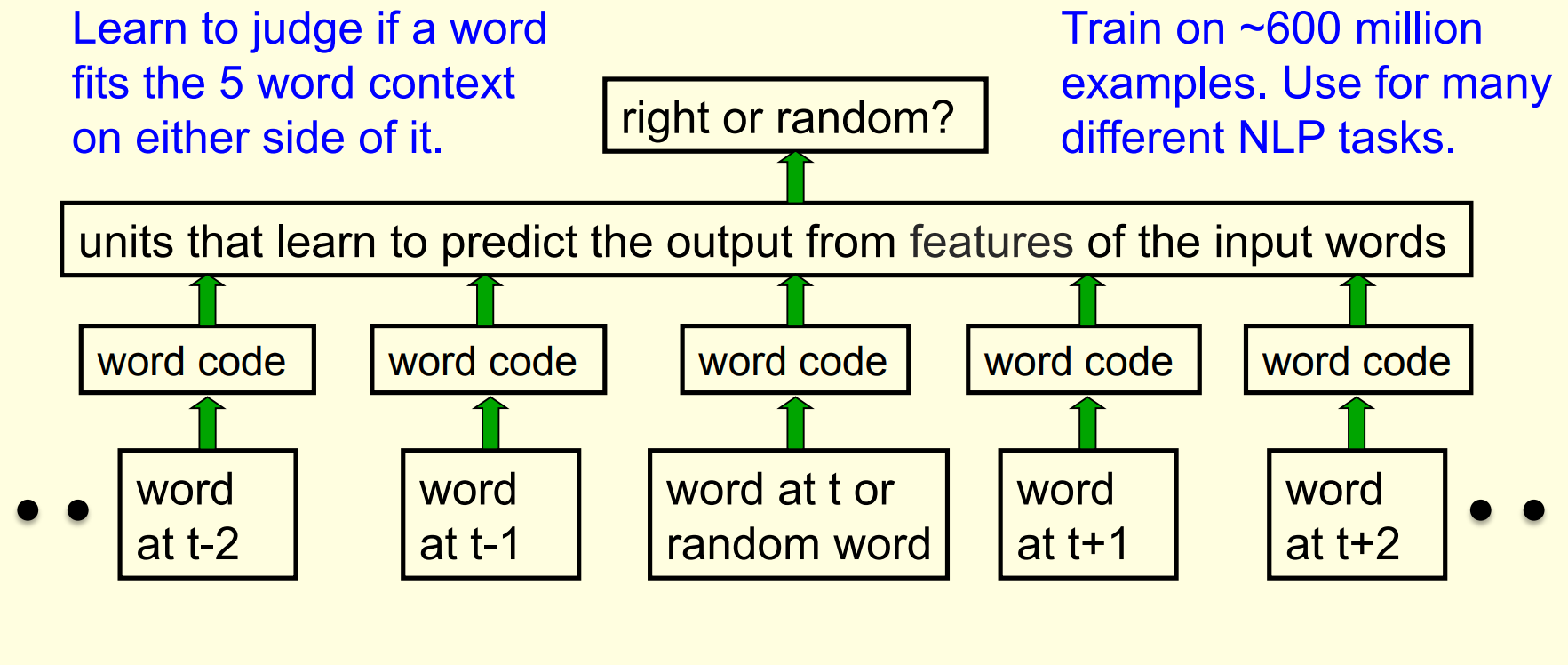
A simpler way to learn feature vectors for words

This method comes from the paper (Collobert and Weston 2008)

Displaying the learned feature vectors in a 2-D map

• We can get an idea of the quality of the learned feature vectors by displaying them in a 2-D map.
  • Display very similar vectors very close to each other.
  • Use a multi-scale method called “t-sne” that also displays similar clusters near each other.
• The learned feature vectors capture lots of subtle semantic distinctions, just by looking at strings of words.
  • No extra supervision required.
  • The information is all in the contexts that the word is used in.
  • Consider “She scrommed him with the frying pan.”

Part of a 2-D map of the 2500 most common words

tsne_output

tsne_output

tsne_output

References

Collobert, Ronan, and Jason Weston. 2008. “A Unified Architecture for Natural Language Processing: Deep Neural Networks with Multitask Learning.” In Proceedings of the 25th International Conference on Machine Learning, 160–67. ICML ’08. New York, NY, USA: Association for Computing Machinery. https://doi.org/10.1145/1390156.1390177.

Mnih, Andriy, Zhang Yuecheng, and Geoffrey Hinton. 2009. “Improving a Statistical Language Model Through Non-Linear Prediction.” Neurocomputing 72 (7-9): 1414–18. https://doi.org/https://doi.org/10.1016/j.neucom.2008.12.025.