Deep Neural Networks - Notes for lecture 4c

Lecture 4c: Another diversion: The Softmax output function

A Softmax cost function is a general-purpose ML component/technique for combining binary discriminators into a probability distribution to construct a classifier We’ve seen binary threshold output neurons and logistic output neurons. This video presents a third type.

This one only makes sense if we have multiple output neurons.

Problems with squared error

• The squared error measure has some drawbacks:
  • If the desired output is 1 and the actual output is 0.00000001 there is almost no gradient for a logistic unit to fix up the error.
  • If we are trying to assign probabilities to mutually exclusive class labels, we know that the outputs should sum to 1, but we are depriving the network of this knowledge.
• Is there a different cost function that works better?
  • Yes: Force the outputs to represent a probability distribution across discrete alternatives

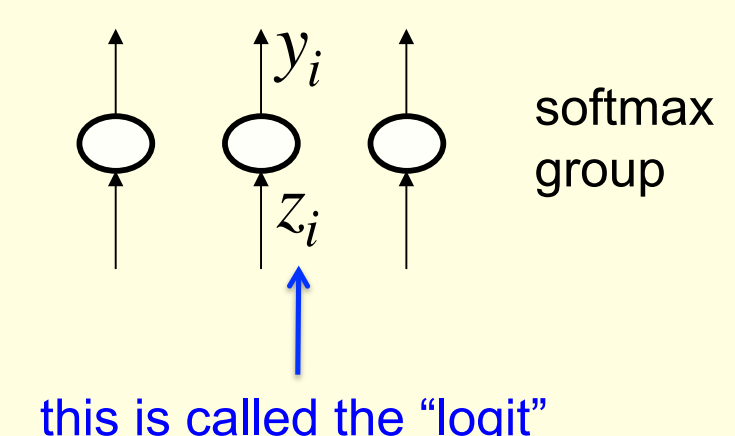
Softmax

The output units in a softmax group use a non-local non-linearity:

y_i = \frac{e^{z_i}}{\sum_{j\in group} e^{z_i}}

\frac{\partial y_i}{\partial z_i} = y_i(1-y_i)

Cross-entropy: the right cost function to use with SoftMax

C=-\sum_j t_j \log y_i \frac {\partial C}{\partial z_i} = - \sum_j t_j \frac {\partial C}{\partial y_i} \frac {\partial y_u}{\partial z_i} = y_i -t_i

• The right cost function is the negative log probability of the right answer.
• C has a very big gradient when the target value is 1 and the output is almost zero.
  • A value of 0.000001 is much better than 0.000000001
  • The steepness of dC/dy exactly balances the flatness of dy/dz

the cross entropy cost function - is the correct cost function to use with SoftMax

Architectural Note:

SoftMax unit +Cross-Entropy loss function => for classification