Deep Neural Networks - Notes for lecture 3e

Lecture 3e: Using the derivatives computed by backpropagation

• The backpropagation algorithm is an efficient way of computing the error derivative \frac{dE}{dw} for every weight on a single training case. There are many decisions needed on how to derive new weights using there derivatives.

  • Optimization issues: How do we use the error derivatives on individual cases to discover a good set of weights? (lecture 6)
  • Generalization issues: How do we ensure that the learned weights work well for cases we did not see during training? (lecture 7)

• We now have a very brief overview of these two sets of issues.

• How often to update weights ?

  • Online - after every case.
  • Mini Batch - after a small sample of training cases.
  • Full Batch - after a full sweep of training data.

• How much to update? (c.f. lecture 6)

  • fixed learning rate
  • adaptable global learning rate
  • adaptable learning rate per weight
  • don’t use steepest descent (velocity/momentum/second order methods)

Overfitting: The downside of using powerful models

• Regularization - How to ensure that learned weights work well for cases we did not see during training?
  
• The training data contains information about the regularities in the mapping from input to output. But it also contains two types of noise.
  • The target values may be unreliable (usually only a minor worry).
  • There is sampling error. There will be accidental regularities just because of the particular training cases that were chosen.
• When we fit the model, it cannot tell which regularities are real and which are caused by sampling error.
  • So it fits both kinds of regularity.
  • If the model is very flexible it can model the sampling error really well. This is a disaster.

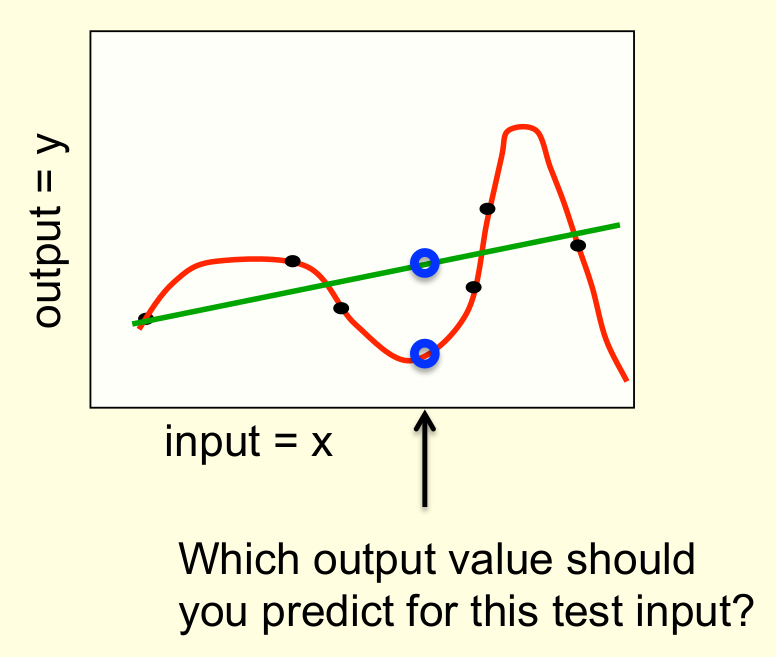
A simple example of overfitting

overfitting

• Which output value should you predict for this test input?
• Which model do you trust?
  • The complicated model fits the data better.
  • But it is not economical.
• A model is convincing when it fits a lot of data surprisingly well.
  • It is not surprising that a complicated model can fit a small amount of data well.
  • Models fit both signal and noise.

How to reduce overfitting

• A large number of different methods have been developed to reduce overfitting.
  • Weight-decay
  • Weight-sharing - reduce model flexibility by adding constraints on weights
  • Early stopping - stop training when by monitoring the Test error.
  • Model averaging - use an ensemble of models
  • Bayesian fitting of neural nets - like averaging but weighed
  • Dropout - (hide data from half the net)
  • Generative pre-training - (more data)
• Many of these methods will be described in lecture 7.