Deep Neural Networks - Notes for lecture 3d

Lecture 3d: The back-propagation algorithm

Here, we start using hidden layers. To train them, we need the back propagation algorithm. Hidden layers, and this algorithm, are very important. They are the layers between the input layer and the output.

The story of training by perturbations also makes an appearance in the course by David MCcay, serving primarily as motivation for the back propagation algorithm.

This computation, just like the forward propagation, can be vectorized across multiple units in every layer, and multiple training cases.

Learning with hidden units (again)

• Networks without hidden units are very limited in the input-output mappings they can model.
• Adding a layer of hand-coded features (as in a Perceptrons) makes them much more powerful but the hard bit is designing the features.
  • We would like to find good features without requiring insights into the task or repeated trial and error where we guess some features and see how well they work.
• We need to automate the loop of designing features for a particular task and seeing how well they work.

Learning by perturbing weights

• Randomly perturb one weight and see if it improves performance. If so, save the change.
  • This is a form of reinforcement learning.
  • Very inefficient. We need to do multiple forward passes on a representative set of training cases just to change one weight. Back propagation is much better.
  • Towards the end of learning, large weight perturbations will nearly always make things worse, because the weights need to have the right relative values. (so we should adapt a decreasing learning rate).
• We could randomly perturb all the weights in parallel and correlate the performance gain with the weight changes.
  • Not any better because we need lots of trials on each training case to “see” the effect of changing one weight through the noise created by all the changes to other weights.
• A better idea: Randomly perturb the activities of the hidden units.
  • Once we know how we want a hidden activity to change on a given training case, we can compute how to change the weights.
  • There are fewer activities than weights, but backpropagation still wins by a factor of the number of neurons.

The idea behind backpropagation

• We don’t know what the hidden units ought to do, but we can compute how fast the error changes as we change a hidden activity.
  • Instead of using desired activities to train the hidden units, use error derivatives w.r.t. hidden activities.
  • Each hidden activity can affect many output units and can therefore have many separate effects on the error. These effects must be combined.
• We can compute error derivatives for all the hidden units efficiently at the same time.
  • Once we have the error derivatives for the hidden activities, its easy to get the error derivatives for the weights going into a hidden unit.

Sketch of back propagation on a single case

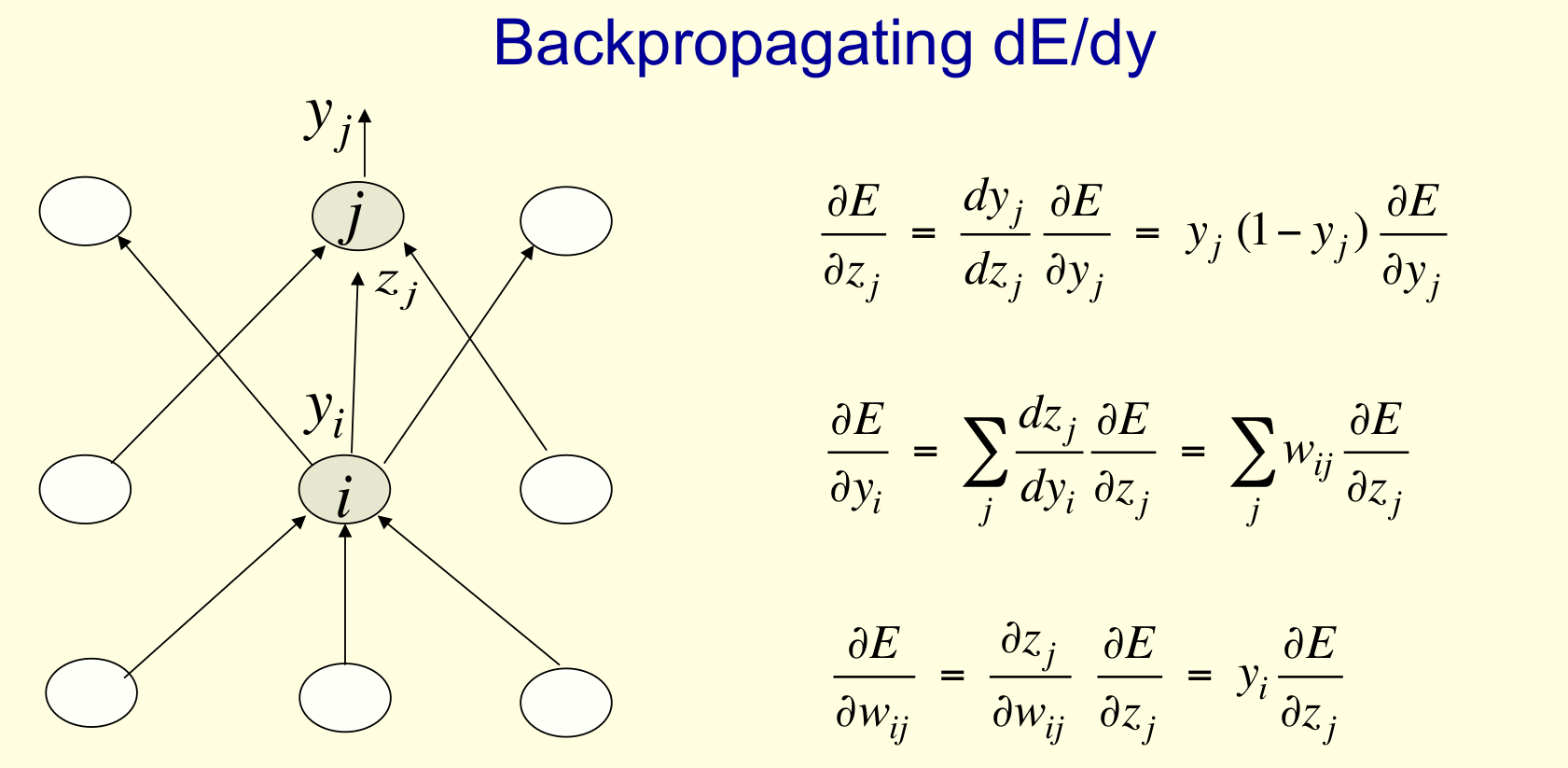
1. First convert the discrepancy between each output and its target value into an error derivative.
2. Then compute error derivatives in each hidden layer from error derivatives in the layer above.
3. Then use error derivatives w.r.t. activities to get error derivatives w.r.t. the incoming weights. E =\frac{1}{2}(t_i-y_i)^2

\frac{\partial E}{\partial y_j}=-(t_j-y_j)

back proogations of errors

backpropagating the error derivative