Lecture 3b: The error surface for a linear neuron

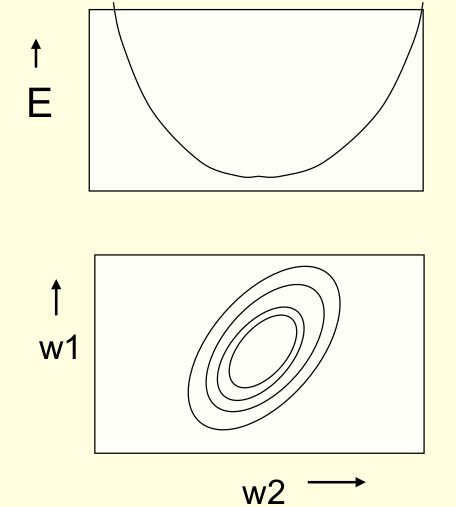
The error surface lies in a space with a horizontal axis for each weight and one vertical axis for the error.
- For a linear neuron with a squared error, it is a quadratic bowl.
- Vertical cross-sections are parabolas.
- Horizontal cross-sections are ellipses.
For multi-layer, non-linear nets the error surface is much more complicated.

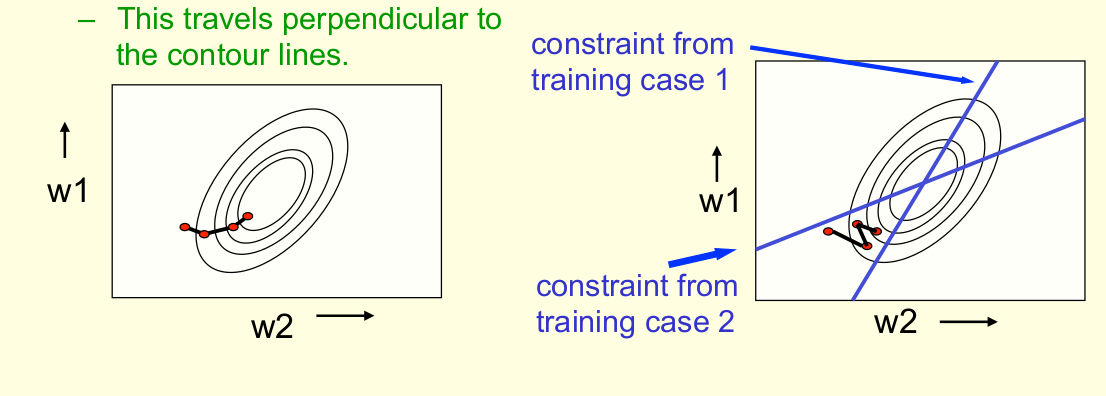
Online versus batch learning

Why learning can be slow

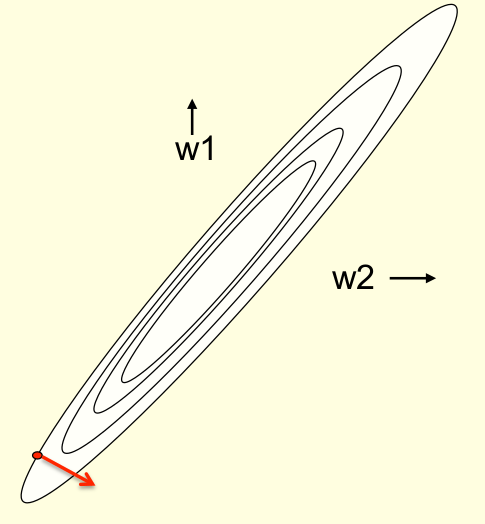
When the ellipse is elongated, the direction of steepest descent is almost perpendicular to the direction towards the minimum!
The red gradient vector has a large component along the short axis of the ellipse and a small component along the long axis of the ellipse.
This is just the opposite of what we want.

Reuse

CC SA BY-NC-ND

Citation

BibTeX citation:

@online{bochman2017,
  author = {Bochman, Oren},
  title = {Deep {Neural} {Networks} - {Notes} for Lecture 3b},
  date = {2017-08-03},
  url = {https://orenbochman.github.io/notes/dnn/dnn-03/l03b.html},
  langid = {en}
}

For attribution, please cite this work as:

Bochman, Oren. 2017. “Deep Neural Networks - Notes for Lecture 3b.” August 3, 2017. https://orenbochman.github.io/notes/dnn/dnn-03/l03b.html.