Deep Neural Networks - Notes for lecture 3a

Lecture 3a: Learning the weights of a linear neuron

Lecure video

Why the perceptron learning procedure cannot be generalised to hidden layers?

• Recall: by convexity, the Perceptron convergence algorithm guarantees that each time the weights change, they get closer to every generously feasible set of weights. 😄
  • This guarantee cannot be extended to more complex networks which wights are non-convex, i.e. the average of two good solutions may be a bad solution. ¹ 😢
• multi-layer neural networks cannot use the perceptron learning procedure.
  • They should never have been called multi-layer perceptrons. ²

A different way to show that a learning procedure makes progress

• Instead of showing the weights get closer to a good set of weights, show that the actual output values get closer the target values.
  • This can be true even for non-convex problems in which there are many quite different sets of weights that work well and averaging two good sets of weights may give a bad set of weights.
  • It is not true for perceptron learning.
• The simplest example is a linear neuron with a squared error measure.

Linear neurons

• Called linear filters in electrical engineering and linear transforms in linear algebra and can be represented by martracies
• We don’t use linear neurons in practice:
  • Without a non-linearity in the unit, a stack of N layers can be replaced by a single layer ³
  • This lecture just demonstrates the analysis we will use with non-linear units.
• The neuron’s output is the real valued weighted sum of its inputs
• The goal of learning is to minimize the total error over all training cases.
  • Here error is the squared difference between the desired output and the actual output.

{\color{green}{\overbrace{y}^{\text{output}}}} = \sum_{n \in train} {\color{red}{\overbrace{w_i}^{\text{weights}}}} {\color{blue}{\underbrace{x_i}_{\text{inputs}}}}= \vec{w}^T\cdot\vec{x} where:

• y is the neuron’s estimate of the desired output
• x is the input vector
• w is the weight vector

Why don’t we solve it analytically?

• It is straight-forward to write down a set of equations, one per training case, and to solve for the best set of weights.
• This is the standard engineering approach so why don’t we use it?
• Scientific answer: We want a method that real neurons could use.
• Engineering answer: We want a method that can be generalized to multi-layer, non-linear neural networks.
• The analytic solution relies on it being linear and having a squared error measure.
• Iterative methods are usually less efficient but they are much easier to generalize.

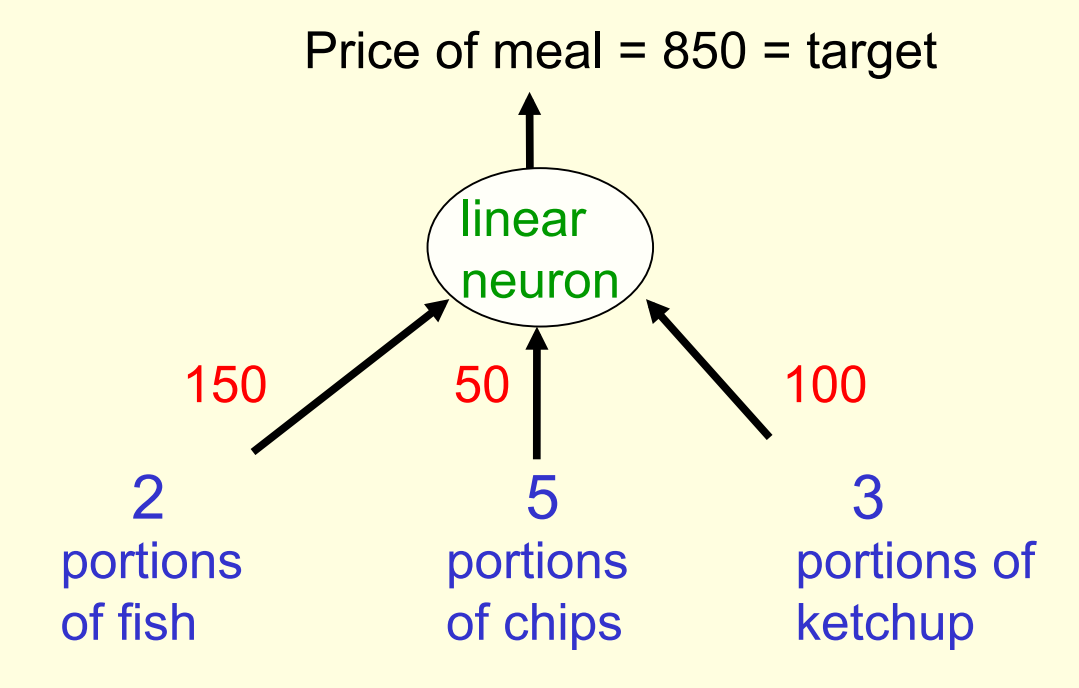
A toy example

• Each day you get lunch at the cafeteria.
  • Your diet consists of fish, chips, and ketchup.
  • You get several portions of each.
• The cashier only tells you the total price of the meal
  • After several days, you should be able to figure out the price of each portion.
• The iterative approach: Start with random guesses for the prices and then adjust them to get a better fit to the observed prices of whole meals.

Solving the equations iteratively

• Each meal price gives a linear constraint on the prices of the portions: \text{price} = X_\text{fish} W_\text{fish} + X_\text{chips} W_\text{chips} + X_\text{ketchup}W_\text{ketchup}
  • The prices of the portions are like the weights in of a linear neuron. W = (w_\text{fish} , W_\text{ chips} , W_\text{ketchup} )
  • We will start with guesses for the weights and then adjust the guesses slightly to give a better fit to the prices given by the cashier.

The true weights used by the cashier

the true weights

• We will start with guesses for the weights and then adjust the guesses slightly to give a better fit to the prices given by the cashier.

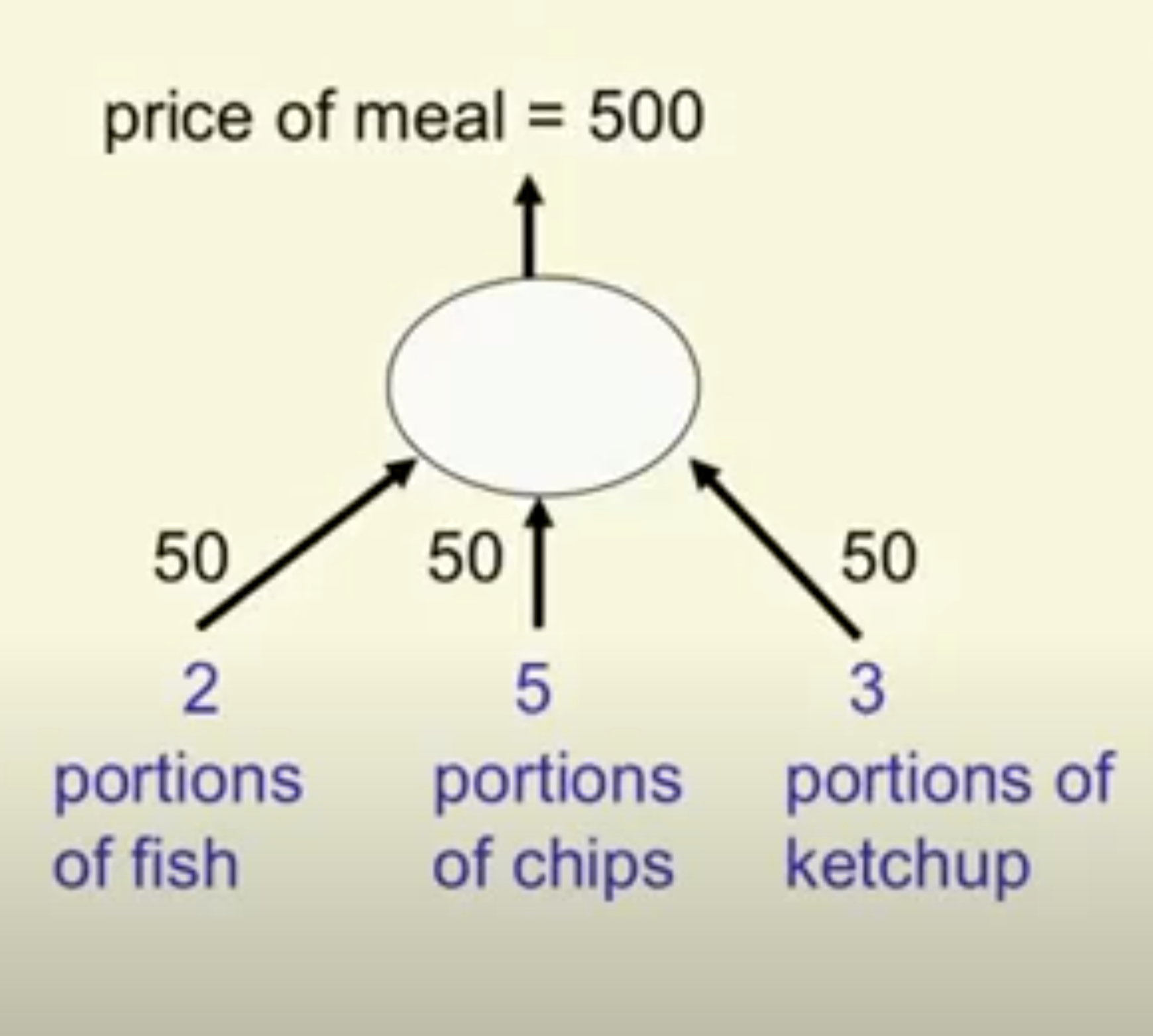
A model of the cashier with arbitrary initial weights

a toy problem

• Residual error = 350
• The “delta-rule” for learning is: \Delta w_i = \epsilon x_i (t - y)
• With a learning rate \epsilon of 1/35, the weight changes are:+20, +50, +30
• This gives new weights of: 70, 100, 80.
• The weight for chips got worse, but over all the weights are better

y reducing errors, individual weight estimate may be getting worse

Calculating the change in the weights:

calculate our output using forward propagation

Deriving the delta rule

y = \sum_{n \in train} w_i x_i= \vec{w}^T\vec{x} Define the error as the squared residuals summed over all training cases:

E = \frac{1}{2}\sum_{n \in train} (t_n−y_n)^2

use the chain rule to get error derivatives for weights

\frac{d E}{\partial w_i}=\frac{1}{2}\sum_{n \in train}\frac{\partial y^n}{\partial w_i} \frac{dE}{dy^n}=\frac{1}{2}\sum_{n \in train}x_i^n(t^n−y^n)

the batch delta rule changes the weight in proportion to their error derivative summed on all training cases times the learning rate

\Delta w_i = −\epsilon \frac{d E}{\partial w_i} = \sum_{n \in train} \epsilon x_i^n (t^n−y^n)

Behaviour of the iterative learning procedure

• Does the learning procedure eventually get the right answer?
  • There may be no perfect answer.
  • By making the learning rate small enough we can get as close as we desire to the best answer.
• How quickly do the weights converge to their correct values?
  • It can be very slow if two input dimensions are highly correlated. If you almost always have the same number of portions of ketchup and chips, it is hard to decide how to divide the price between ketchup and chips

The relationship between the online delta-rule and the learning rule for perceptrons

• In perceptron learning, we increment or decrement the weight vector by the input vector.
  • But we only change the weights when we make an error.
• In the online version of the delta-rule we increment or decrement the weight vector by the input vector scaled by the residual error and the learning rate.
  • So we have to choose a learning rate. This is annoying

residual error

it’s the amount by which we got the answer wrong.

A very central concept is introduced without being made very explicit: we use derivatives for learning, i.e. for making the weights better. Try to understand why those concepts are indeed very related.

on-line learning

means that we change the weights after every training example that we see, and we typically cycle through the collection of available training examples.

Footnotes

1. a convex set includes all weighted sums

2. no one calls them that anymore

3. think multiplying N-matracies just gives a single matrix