Now we consider why we don’t use Perceptrons
namely their short comings
Lecture 2e: What Perceptrons can not do
The limitations of Perceptrons
- If you are allowed to choose the features by hand and if you use enough features, you can do almost anything.
- For binary input vectors, we can have a separate feature unit for each of the exponentially many binary vectors and so we can make any possible discrimination on binary input vectors.
- This type of table look-up won’t generalize.
- But once the hand-coded features have been determined, there are very strong limitations on what a perceptron can learn.
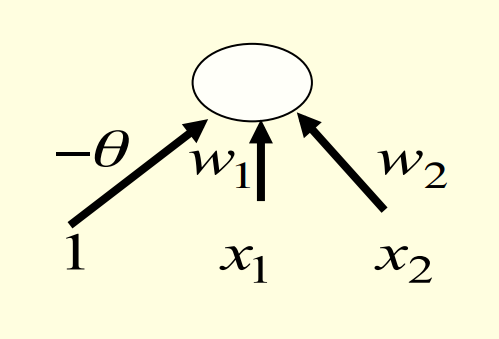
What binary threshold neurons cannot do
- A binary threshold output unit cannot even tell if two single bit features are the same!
| case | map | map |
|---|---|---|
| Positive cases (same) | (1,1) \to 1 | (0,0) \to 1 |
| Negative cases (different) | (1,0) \to 0 | (0,1) \to 0 |
The four input-output pairs give four inequalities that are impossible to satisfy:
w_1+w_2 \ge \theta \qquad \theta \ge 0
w_1 < \theta \qquad w_2 < \theta
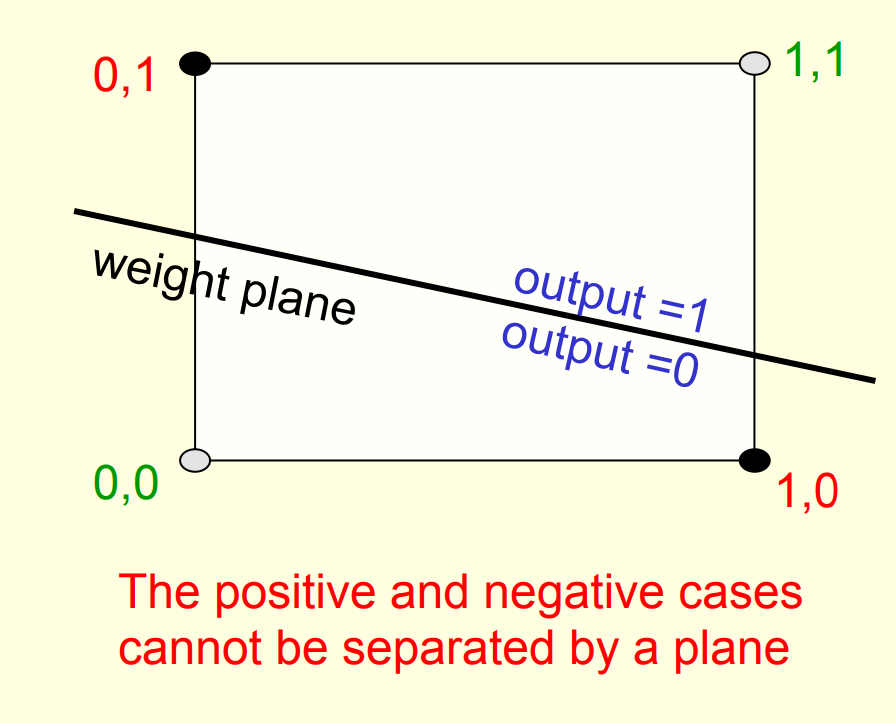
A geometric view of what binary threshold neurons cannot do
Imagine “data-space” in which the axes correspond to components of an input vector.
- Each input vector is a point in this space.
- A weight vector defines a plane in data-space.
- The weight plane is perpendicular to the weight vector and misses the origin by a distance equal to the threshold.
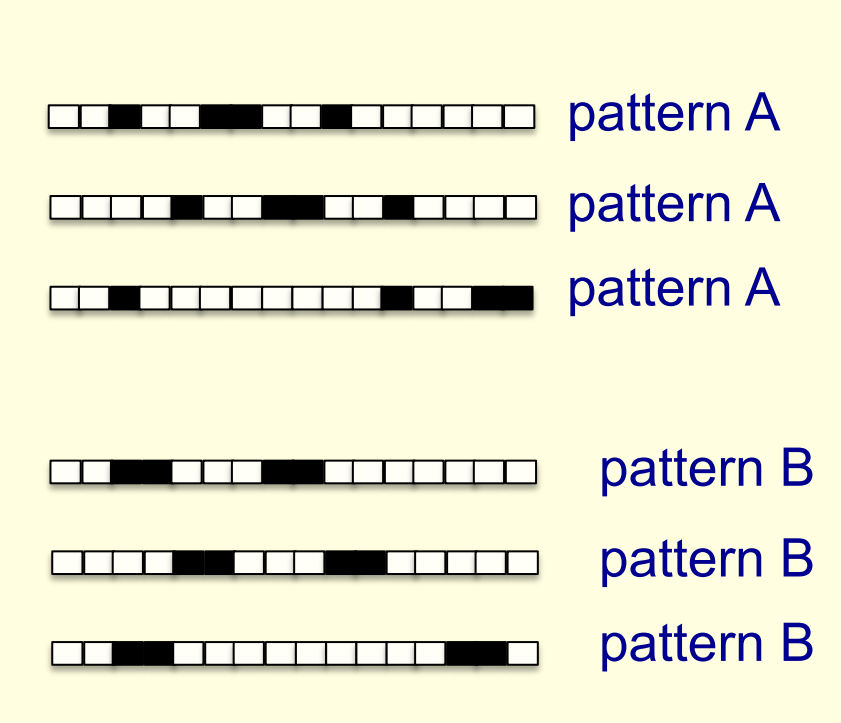
Discriminating simple patterns under translation with wrap-around
- Suppose we just use pixels as the features.
- Can a binary threshold unit discriminate between different patterns that have the same number of on pixels?
- Not if the patterns can translate with wrap-around!
Sketch of a proof that a binary decision unit cannot discriminate patterns with the same number of on pixels (assuming translation with wraparound)
- For pattern A, use training cases in all possible translations.
- Each pixel will be activated by 4 different translations of pattern A.
- So the total input received by the decision unit over all these patterns will be four times the sum of all the weights.
- For pattern B, use training cases in all possible translations.
- Each pixel will be activated by 4 different translations of pattern B.
- So the total input received by the decision unit over all these patterns will be four times the sum of all the weights.
- But to discriminate correctly, every single case of pattern A must provide more input to the decision unit than every single case of pattern B.
- This is impossible if the sums over cases are the same.
Why this result was devastating for Perceptrons
- The whole point of pattern recognition is to recognize patterns despite transformations like translation.
- In thier book Minsky and Papert (1969) the authors Marvin Minsky and Seymour Papert proove the Group Invariance Theorem which says that the part of a Perceptron that learns cannot learn to do this if the transformations form a group.
- Translations with wrap-around form a group.
- To deal with such transformations, a Perceptron needs to use multiple feature units to recognize transformations of informative sub-patterns.
- So the tricky part of pattern recognition must be solved by the hand-coded feature detectors, not the learning procedure.
References
Minsky, Marvin, and Seymour Papert. 1969. Perceptrons: An Introduction to Computational Geometry. Cambridge, MA, USA: MIT Press.
Reuse
CC SA BY-NC-ND
Citation
BibTeX citation:
@online{bochman2017,
author = {Bochman, Oren},
title = {Deep {Neural} {Networks} - {Notes} for Lecture 2e},
date = {2017-07-21},
url = {https://orenbochman.github.io/notes/dnn/dnn-02/l02e.html},
langid = {en}
}
For attribution, please cite this work as:
Bochman, Oren. 2017. “Deep Neural Networks - Notes for Lecture
2e.” July 21, 2017. https://orenbochman.github.io/notes/dnn/dnn-02/l02e.html.