Deep Neural Networks - Notes for lecture 2d

In this lecture we try to explain intuitively why the perceptron algorithm works

Also we consider why it may fail.

Lecture 2d: Why the learning works?

Why the learning procedure works (first attempt)

idea of the proof

we want to get closer all the feasible solution

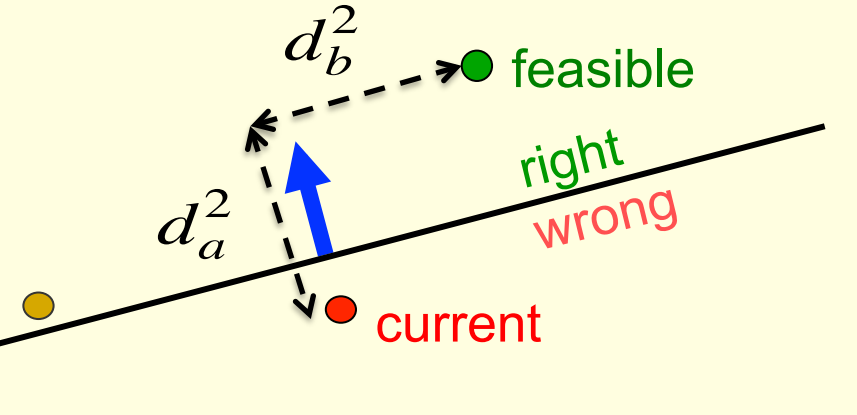
Consider the squared distance d_a^2+d_b^2 between any feasible weight vector and the current weight vector. – Hopeful claim: Every time the perceptron makes a mistake, the learning algorithm moves the current weight vector closer to all feasible weight vectors

We look at the geometrical interpretation which is the proof for the convergence of the Perceptron learning algorithm works. We are trying to find a decision surface by solving a convex optimization problem.

The surface is a hyper-plane represented by a line where on side is the correct set and the other is incorrect. The weight vectors form a cone:

• This means that wights are closed under addition and positive scaler product.
• At zero it is zero.

fixing it up

we now use a generously feasible sub-cone of the feasible cone shown in a dotted line

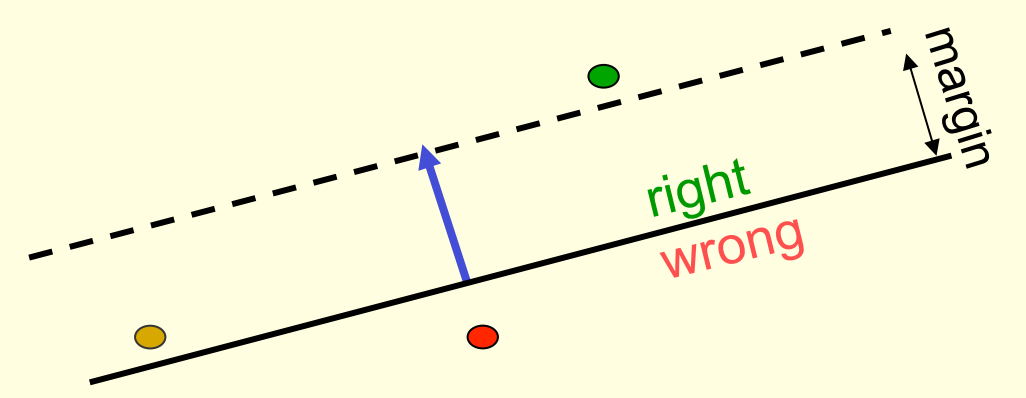
• So consider “generously feasible” weight vectors that lie within the feasible region by a margin at least as great as the length of the input vector that defines each constraint plane.
  • Every time the perceptron makes a mistake, the squared distance to all of these generously feasible weight vectors is always decreased by at least the squared length of the update vector.

Informal sketch of proof of convergence

• Each time the perceptron makes a mistake, the current weight vector moves to decrease its squared distance from every weight vector in the “generously feasible” region.
• The squared distance decreases by at least the squared length of the input vector.
• So after a finite number of mistakes, the weight vector must lie in the feasible region if this region exists.