Deep Neural Networks - Notes for lecture 2c

Lecture 2c: A geometrical view of perceptrons

Warning!

• For non-mathematicians, this is going to be tougher than the previous material.
• You may have to spend a long time studying the next two parts.
• If you are not used to thinking about hyper-planes in high-dimensional spaces, now is the time to learn.
• To deal with hyper-planes in a 14-dimensional space, visualize a 3-D space and say “fourteen” to yourself very loudly. Everyone does it. :-)
  • But remember that going from 13-D to 14-D creates as much extra complexity as going from 2-D to 3-D.

Geometry review

• A point (a.k.a. location) and an arrow from the origin to that point, are often used interchangeably.
• A hyperplane is the high-dimensional equivalent of a plane in 3-D.
• The scalar product or inner product between two vectors
  • sum of element-wise products.
  • The scalar product between two vectors that have an angle of less than 90 degrees between them is positive.
  • For more than 90 degrees it’s negative.

Weight-space

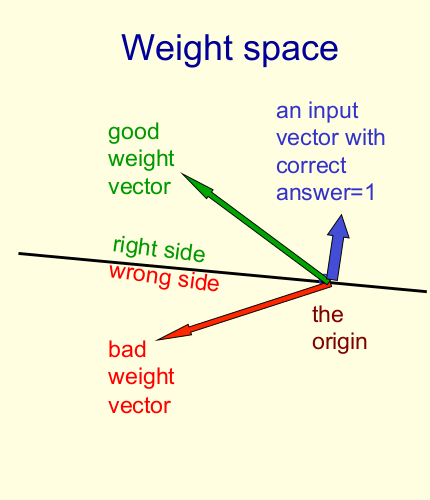
Weight-space

• This space has one dimension per weight.
• A point in the space represents a particular setting of all the weights.
• Assuming that we have eliminated the threshold, each training case can be represented as a hyperplane through the origin.
  • The weights must lie on one side of this hyper-plane to get the answer correct.
• Each training case defines a plane (shown as a black line)
  • The plane goes through the origin and is perpendicular to the input vector.
  • On one side of the plane the output is wrong because the scalar product of the weight vector with the input vector has the wrong sign.

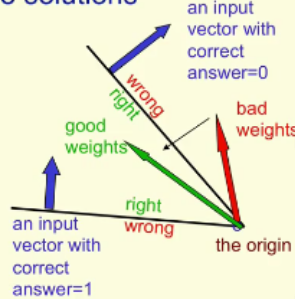
The cone of feasible solutions

Cone of feasable soulutions

• To get all training cases right we need to find a point on the right side of all the planes.
  • There may not be any such point!
• If there are any weight vectors that get the right answer for all cases, they lie in a hyper-cone with its apex at the origin.
  • So the average of two good weight vectors is a good weight vector.
    • The problem is convex.

This is not a very good explanation - unless we also take a convex optimization course in which we define a hyperplane and a cone.