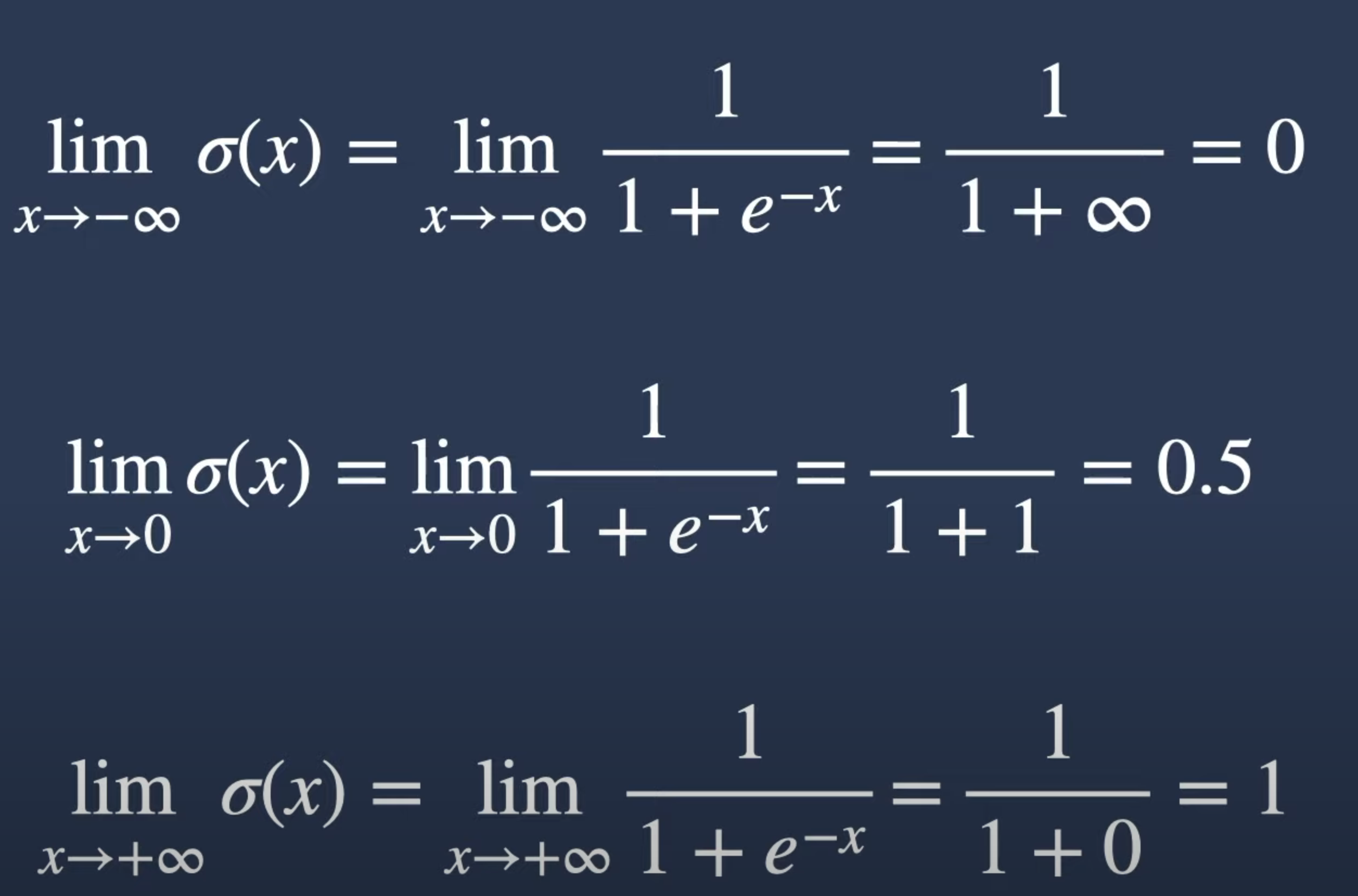Whate’er the theme, the Maiden sang
As if her song could have no ending;
I saw her singing at her work,
And o’er the sickle bending;—
I listened, motionless and still;
And, as I mounted up the hill,
The music in my heart I bore,
Long after it was heard no more.– The Solitary Reaper by William Wordsworth.
- Just when we think that the transformer rules supreme the RNN makes a comeback with a refreshing new look at the LSTMs.
- This paper brings new architectures to the LSTM that are fully parallelizable and can scale to billions of parameters.
- They demonstrate on synthetic tasks and language modeling benchmarks that these new xLSTMs can outperform state-of-the-art Transformers and State Space Models.
Introduction
So this is my first review of the RNN papers. I found that since the courses covering LSTM seemed to be over simplified and confusing, I should go back to the source. Since time is limited, it helps to review the papers in reverse chronological order. Each new papers explains the limitations that are generally not apparent when the paper is first published. The authors of the later papers also have the benefit of hindsight which they share in the obligatory literature review wherein they provide lots of context we cannot get by reading the original papers. Given all that there is also a benefit to reading the original paper - the real innovators while harder to understand are remarkable thinkers and often reveal motivations and deep insights that elude later interlocutors.
Podcast & Other Reviews
This paper is a bit heavy on the technical side. But if we are still here, we may enjoy this podcast reviewing the paper. Though AI generated I found it quite useful to get oriented with the paper and understand that the experiments the authors run to validate this new architectures.
We also cover something I found absent from the Course on sequence models . The limitations of LSTMs as viewed by the authors when considered in the context of transformers and Mamba.
Although this paper is recent there are a number of other people who cover it.
- In Video 2 Yannic Kilcher covers the paper in his youtube channel. He does a great job of explaining the paper in a way that is easy to understand. Kilcher is all too human, he makes many mistakes, stresses opinions over facts. If we don’t mind all that he is a great resource for understanding the paper. I find he rubs me the wrong way but at least I find this motivating to do better in my own reviews!
xLSTM has the potential to considerably impact other fields like Reinforcement Learning, Time Series Prediction, or the modeling of physical systems. – (Beck et al. 2024)
In his book Understanding Media (McLuhan 1988) Marshal McLuhan introduced his Tetrad. The Tetrad is a mental model for understanding how a technological innovation like the xLSTM might disrupt society. To work the model we ask the following four questions that can be applied to any new technology to understand its impact. The four questions in this instance are:
- What does the xLSTM enhance or amplify?
The xLSTM enhances the LSTM by introducing exponential gating and novel memory structures, boosting its capabilities to perform favorably when compared to state-of-the-art Transformers and State Space Models.
- What does the xLSTM make obsolete or replace?
The xLSTM makes the traditional LSTM obsolete by addressing its limitations, such as the inability to revise storage decisions, limited storage capacities, and lack of parallelizability.
- What does the xLSTM retrieve that was previously obsolesced?
The xLSTM retrieves the LSTM’s relevance in large-scale language modeling by scaling it to billions of parameters and integrating modern LLM techniques while mitigating known limitations. 4. What does the xLSTM reverse or flip into when pushed to its limits?
The xLSTM, when pushed to its limits, can compete with current Large Language Models based on Transformer technology, offering a competitive alternative for sequence modeling tasks.
The xLSTM paper by (Beck et al. 2024) is a great example of the tetrad in action. The authors take the LSTM, a technology that has stood the test of time, and enhance it with exponential gating and novel memory structures. They address the limitations of traditional LSTMs and push the technology to new limits, creating a new architecture that can compete with state-of-the-art Transformers and State Space Models. Recent work by (Chen et al. 2024) suggest that Transformers and The State Space Models are actually limited in their own ways.
Abstract
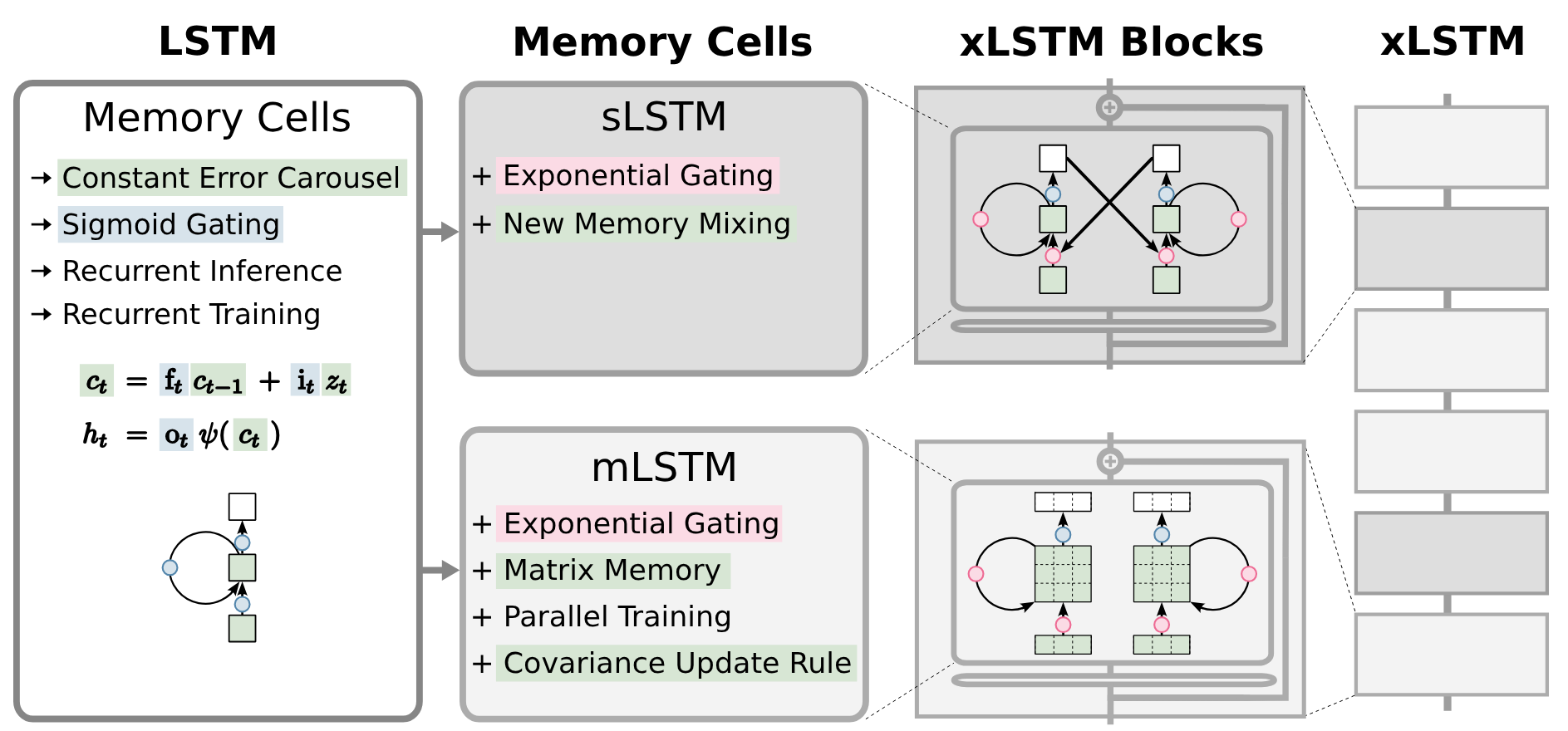
In the 1990s, the constant error carousel and gating were introduced as the central ideas of the Long Short-Term Memory (LSTM). Since then, LSTMs have stood the test of time and contributed to numerous deep learning success stories, in particular they constituted the first Large Language Models (LLMs). However, the advent of the Transformer technology with parallelizable self-attention at its core marked the dawn of a new era, outpacing LSTMs at scale. We now raise a simple question: How far do we get in language modeling when scaling LSTMs to billions of parameters, leveraging the latest techniques from modern LLMs, but mitigating known limitations of LSTMs? Firstly, we introduce exponential gating with appropriate normalization and stabilization techniques. Secondly, we modify the LSTM memory structure, obtaining:
- sLSTM with a scalar memory, a scalar update, and new memory mixing,
- mLSTM that is fully parallelizable with a matrix memory and a covariance update rule.
Integrating these LSTM extensions into residual block backbones yields xLSTM blocks that are then residually stacked into xLSTM architectures. Exponential gating and modified memory structures boost xLSTM capabilities to perform favorably when compared to state-of-the-art Transformers and State Space Models, both in performance and scaling. — (Beck et al. 2024)
1. The original LSTM memory cell with constant error carousel and gating.
2. New sLSTM and mLSTM memory cells that introduce exponential gating. sLSTM offers a new memory mixing technique. mLSTM is fully parallelizable with a novel matrix memory cell state and new covariance update rule.
3. mLSTM and sLSTM in residual blocks yield xLSTM blocks.
4. Stacked xLSTM blocks give an xLSTM
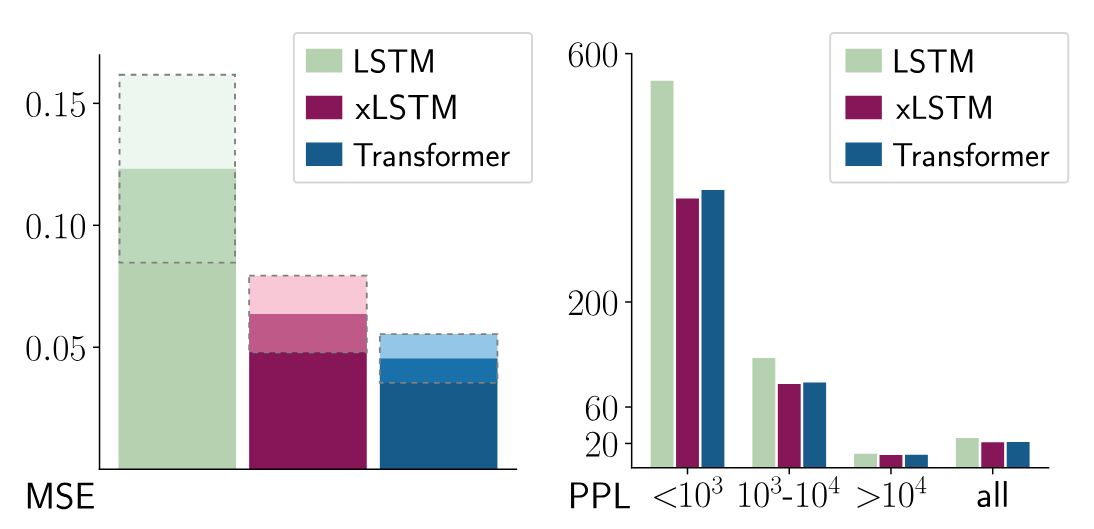
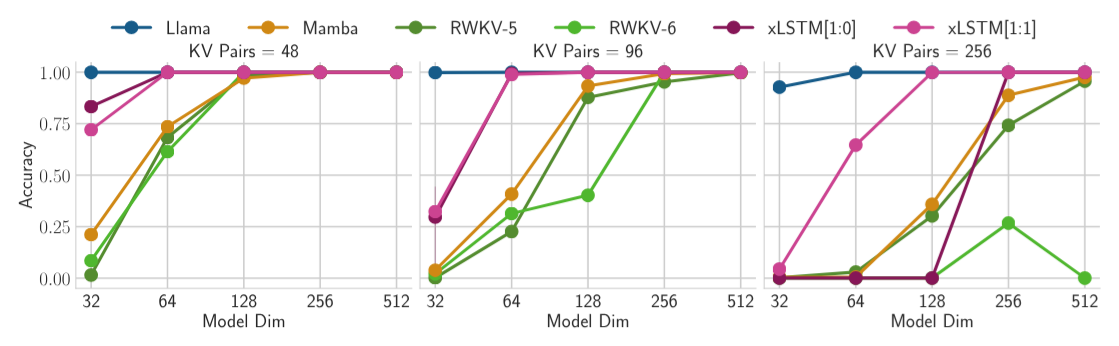
- Left: Nearest Neighbor Search problem in terms of mean squared error (MSE). Given a reference vector, a sequence is scanned sequentially for the most similar vector with the objective to return its attached value at sequence end. LSTM struggles to revise a stored value when a more similar vector is found. Our new xLSTM overcomes this limitation by exponential gating. - Right: Rare Token Prediction. The perplexity (PPL) of token prediction on Wikitext-103, in partitions of token frequency. LSTM performs worse on predicting rare tokens because of its limited storage capacities, whereas our new xLSTM solves this problem via a matrix memory.
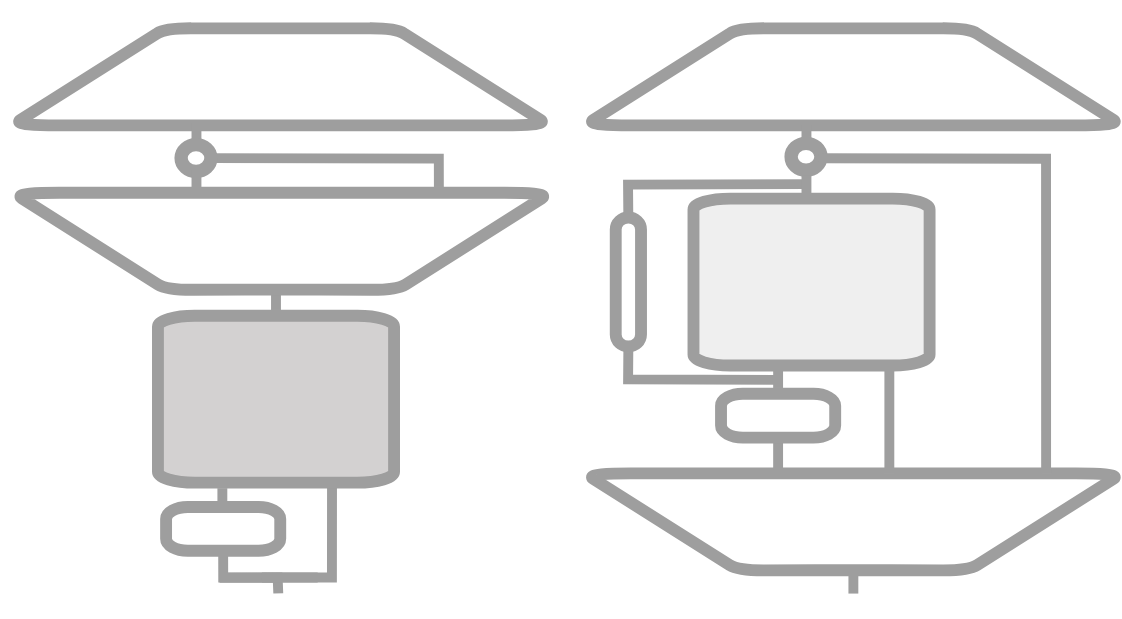
Left: A residual sLSTM block with post up-projection (like Transformers): The input is fed into an sLSTM — with an optional convolution — followed by a gated MLP.
Right: A residual mLSTM block with pre up-projection (like State Space models): mLSTM is wrapped inside two MLPs, via a convolution, a learnable skip connection, and an output gate that acts componentwise.
Left: A residual sLSTM block with post up-projection (like Transformers): The input is fed into an sLSTM — with an optional convolution — followed by a gated MLP.
Right: A residual mLSTM block with pre up-projection (like State Space models): mLSTM is wrapped inside two MLPs, via a convolution, a learnable skip connection, and an output gate that acts componentwise.
Left: A residual sLSTM block with post up-projection (like Transformers): The input is fed into an sLSTM — with an optional convolution — followed by a gated MLP.
Right: A residual mLSTM block with pre up-projection (like State Space models): mLSTM is wrapped inside two MLPs, via a convolution, a learnable skip connection, and an output gate that acts componentwise.
Paper Outline
- Introduction
- Describes the constant error carousel and gating mechanisms of Long Short-Term Memory (LSTM). > “In the 1990s, the constant error carousel and gating were introduced as the central ideas of the Long Short-Term Memory (LSTM). Since then, LSTMs have stood the test of time and contributed to numerous deep learning success stories…”
- Discusses three main limitations of LSTMs:
- The inability to revise storage decisions.
- Limited storage capacities.
- Lack of parallelizability due to memory mixing.
- Highlights the emergence of Transformers in language modeling due to these limitations. > Transformer Era: The rise of Transformers with parallelizable self-attention has largely overshadowed LSTMs due to their superior scalability.
- Extended Long Short-Term Memory
- Introduces Extended Long Short-Term Memory (xLSTM), which incorporates exponential gating and novel memory structures.
- Presents two new LSTM variants:
- sLSTM with a scalar memory, a scalar update, and new memory mixing.
- mLSTM with a matrix memory and a covariance update rule, which is fully parallelizable.
- Describes the integration of these LSTM variants into residual block modules, resulting in xLSTM blocks.
- Presents xLSTM architectures that residually stack xLSTM blocks.
- Related Work:
- Mentions various linear attention methods to overcome the quadratic complexity of Transformer attention.
- Notes the popularity of State Space Models (SSMs) for language modeling.
- Highlights the use of Recurrent Neural Networks (RNNs) as a replacement for Transformers.
- Mentions the use of gating in recent RNN and SSM approaches.
- Notes the use of covariance update rules1 to enhance storage capacities in various models.
- Experiments
- Presents the experimental evaluation of xLSTM compared to existing methods with a focus on language modeling.
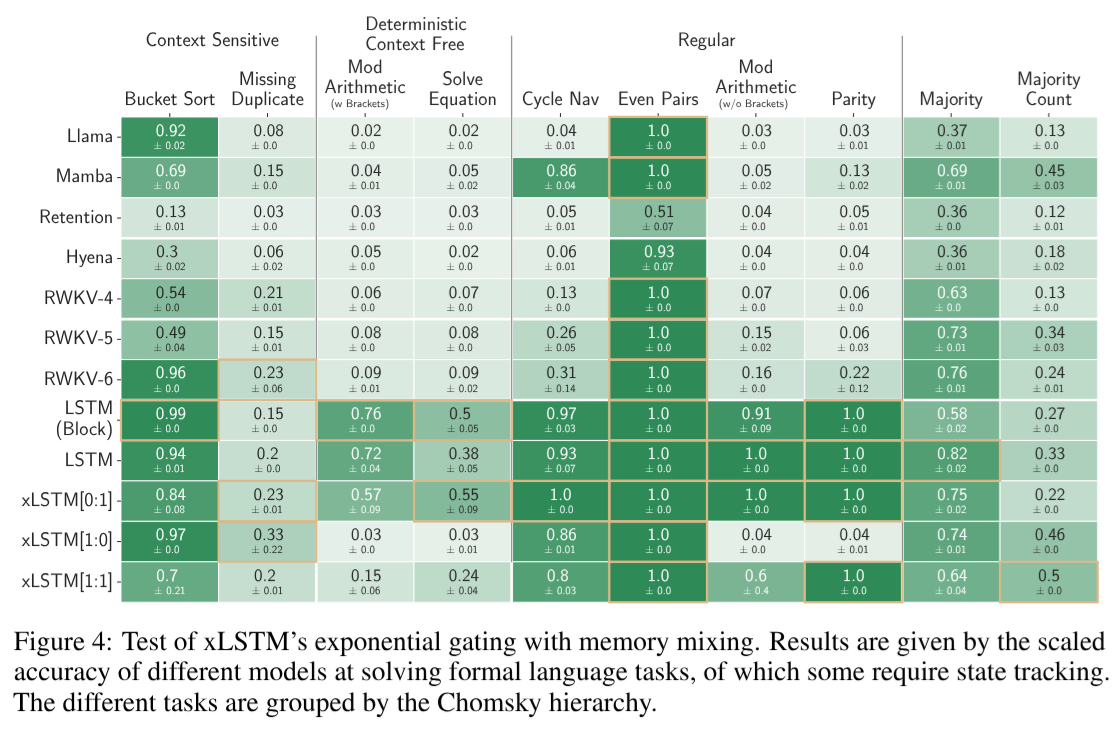
- Discusses the effectiveness of xLSTM on synthetic tasks, including:
- Formal languages.
- Multi-Query Associative Recall.
- Long Range Arena tasks.
- Presents a method comparison and ablation study, where different models are trained on 15 billion tokens from the SlimPajama dataset.
- Assesses the scaling behavior of different methods based on validation perplexity.
- Conducts a large-scale language modeling experiment:
- Training different model sizes on 300B tokens from SlimPajama.
- Evaluating models on length extrapolation.
- Assessing models on validation perplexity and performance on downstream tasks.
- Evaluating models on 571 text domains of the PALOMA language benchmark dataset.
- Assessing the scaling behavior with increased training data.
- Limitations
- Highlights limitations of xLSTM, including:
- Lack of parallelizability for sLSTM due to memory mixing.
- Unoptimized CUDA kernels for mLSTM.
- High computational complexity of mLSTM’s matrix memory.
- Memory overload for longer contexts due to the independence of mLSTM’s memory from sequence length.
- Highlights limitations of xLSTM, including:
- Conclusion
- Concludes that xLSTM performs favorably in language modeling compared to Transformers and State Space Models.
- Suggests that larger xLSTM models will be competitive with current Large Language Models based on Transformer technology.
- Notes the potential impact of xLSTM on other deep learning fields such as reinforcement learning, time series prediction, and physical system modeling.
1 explain covariance
Briefing : xLSTM - Extended Long Short-Term Memory
Introduction and Motivation:
LSTM’s Legacy: The Long Short-Term Memory (LSTM), introduced in the 1990s, has been a cornerstone of deep learning, especially in sequence modeling and early Large Language Models (LLMs). LSTMs are known for their “constant error carousel” and gating mechanisms, designed to combat vanishing gradients in recurrent neural networks.
“In the 1990s, the constant error carousel and gating were introduced as the central ideas of the Long Short-Term Memory (LSTM). Since then, LSTMs have stood the test of time and contributed to numerous deep learning success stories…”
Transformer Era: The rise of Transformers with parallelizable self-attention has largely overshadowed LSTMs due to their superior scalability.
“However, the advent of the Transformer technology with parallelizable self-attention at its core marked the dawn of a new era, outpacing LSTMs at scale.” xLSTM Question: This research aims to explore the capabilities of LSTMs when scaled to billions of parameters, by integrating modern LLM techniques while addressing known limitations.
“We now raise a simple question: How far do we get in language modeling when scaling LSTMs to billions of parameters, leveraging the latest techniques from modern LLMs, but mitigating known limitations of LSTMs?”
Key Limitations of Traditional LSTMs:
The paper identifies three major limitations of traditional LSTMs:
- Inability to Revise Storage Decisions: LSTMs struggle to update previously stored information when more relevant information arrives later in the sequence. The paper uses a “Nearest Neighbor Search” task to demonstrate this.
“LSTM struggles to revise a stored value when a more similar vector is found…”
- Limited Storage Capacity: LSTMs store information in scalar cell states, which can lead to information compression and loss. This impacts performance on tasks requiring detailed memory, like predicting rare tokens.
“LSTM performs worse on predicting rare tokens because of its limited storage capacities…”
- Lack of Parallelizability: LSTMs process data sequentially due to the recurrent connections between hidden states, hindering parallel computation.
“Lack of parallelizability due to memory mixing, i.e., the hidden-hidden connections between hidden states from one time step to the next, which enforce sequential processing.”
- xLSTM Innovations:
The paper introduces Extended Long Short-Term Memory (xLSTM), designed to address the above limitations, by modifying the original LSTM using two main approaches:
Exponential Gating:Implemented to allow for better revision of storage decisions. Normalization and stabilization techniques are used to avoid overflows in calculations due to the exponential function.
“To empower LSTMs with the ability to revise storage decisions, we introduce exponential gates (red) together with normalization and stabilization.” Novel Memory Structures: Two new LSTM variants are created with these structures:
sLSTM: A scalar memory LSTM with a scalar update and new memory mixing technique (within heads, not across). Features multiple memory cells and multiple heads, with memory mixing within each head.
“The new sLSTM (see Section 2.2) with a scalar memory, a scalar update, and memory mixing…”
mLSTM: A matrix memory LSTM, fully parallelizable, with a covariance update rule for storing key-value pairs. Does not have memory mixing between cells or heads.
“the new mLSTM (see Section 2.3) with a matrix memory and a covariance (outer product) update rule, which is fully parallelizable.”
- sLSTM Details:
- Exponential Gates: Introduces exponential activation functions for input and forget gates with normalization and a stabilizer state to prevent overflow.
- Normalizer State: A state used to normalize the hidden state output by accumulating a weighted sum of input and forget gates.
- Memory Mixing: sLSTM allows memory mixing between cells, and also introduces a new form of memory mixing through multiple heads, mixing between cells within a head, but not across heads.
“The new sLSTM can have multiple heads with memory mixing within each head but not across heads. The introduction of heads for sLSTM together with exponential gating establishes a new way of memory mixing.”
- mLSTM Details:
Matrix Memory: Replaces the scalar cell state with a matrix, increasing storage capacity.
Key-Value Storage: The mLSTM memory is based around a key-value storage system inspired by Bidirectional Associative Memories (BAMs) using covariance updates, where keys and values are updated via an outer product.
“At time t, we want to store a pair of vectors, the key k_t ∈ R^d and the value v_t ∈ R^d… The covariance update rule… for storing a key-value pair…”
Parallelization: mLSTM is fully parallelizable due to abandoning hidden-hidden recurrent connections and memory mixing. Computations can be performed efficiently on GPUs using standard matrix operations.
“…the mLSTM… which is fully parallelizable.”
- xLSTM Architecture:
xLSTM Blocks: The sLSTM and mLSTM variants are integrated into residual blocks.
sLSTM blocks use post up-projection (like Transformers).
mLSTM blocks use pre up-projection (like State Space Models).
“Integrating these new LSTM variants into residual block modules results in xLSTM blocks…”
Residual Stacking: xLSTM architectures are created by residually stacking these blocks, using pre-LayerNorm backbones similar to current LLMs.
“An xLSTM architecture is constructed by residually stacking build-ing blocks…” Cover’s Theorem: Used to justify mapping information into a higher-dimensional space for better separation of histories or contexts.
“We resort to Cover’s Theorem (Cover, 1965), which states that in a higher dimensional space non-linearly embedded patterns can more likely be linearly separated than in the original space.”
- Performance and Scaling:
Linear Computation & Constant Memory: Unlike Transformers, xLSTM networks have linear computation and constant memory complexity with respect to sequence length.
“Contrary to Transformers, xLSTM networks have a linear computation and a constant memory complexity with respect to the sequence length.”
Synthetic Tasks: xLSTM showed improved performance over regular LSTMs on “Nearest Neighbor Search” and “Rare Token Prediction” synthetic tasks.
SlimPajama Experiments: The xLSTM models were trained on 15B and 300B tokens from the SlimPajama dataset for language modelling evaluation.
Competitive Performance: xLSTMs demonstrate competitive performance against state-of-the-art Transformers and State Space Models on language modelling benchmarks, both in terms of next token prediction perplexity and downstream tasks.
“Exponential gating and modified memory structures boost xLSTM capabilities to perform favorably when compared to state-of-the-art Transformers and State Space Models, both in performance and scaling.”
Ablation studies show importance of gating techniques.
- Memory & Speed:
sLSTM: Not parallelizable due to memory mixing, although the authors have created a fast CUDA implementation (less than twice as slow as mLSTM).
“While mLSTM is parallelizable analog to FlashAttention… sLSTM is not parallelizable due to the memory mixing…”
mLSTM: Parallelizable, but currently slower than FlashAttention or Mamba due to non-optimized CUDA kernels. Matrix memory is computationally complex but does not require parameters and can be parallelized.
“The memory of mLSTM does not require parameters but is computationally expensive through its d×d matrix memory and d× d update… the computations can be done in parallel on GPUs, therefore these computations have only a minor effect on the wall clock time.”
- Limitations:
sLSTM Parallelization: sLSTM’s memory mixing is non-parallelizable.
“(i) In contrast to mLSTM, memory mixing of the sLSTM prohibits parallelizable operations, and therefore does not allow a fast parallel implementation.”
mLSTM CUDA Optimization: The mLSTM CUDA kernels are not fully optimized.
“(ii) The CUDA kernels for mLSTM are not optimized, and therefore the current implementation is about 4 times slower than FlashAttention or the scan used in Mamba.”
mLSTM Matrix Memory: High computational complexity for mLSTM due to matrix memory operations.
Forget Gate Initialization: Careful initialization of the forget gates is needed.
Long Context Memory: The matrix memory is independent of sequence length, and might overload memory for long context sizes.
“(v) Since the matrix memory is independent of the sequence length, increasing the sequence length might overload the memory for longer context sizes.”
Hyperparameter Optimization: xLSTM is not yet fully optimized due to computational load, indicating further performance gains are possible.
“(vi) Due to the expensive computational load for large language experiments, we did neither fully optimize the architecture nor the hyperparameters, especially for larger xLSTM architectures.”
- Related Work:
The paper highlights connections of its ideas with the following areas:
Gating: Many recent models such as HGRN, GLA, Gated State Space models, Mamba, and others also utilize gating mechanisms. Covariance Update Rule: The covariance update rule used in mLSTM is related to other methods such as Fast Weight Programmers, Retention, and Linear Transformers.
- Conclusion:
The xLSTM presents a compelling alternative to Transformers in sequence modeling, especially in contexts where memory efficiency and longer sequences are required. By combining insights from the original LSTM with exponential gating and novel memory structures, the paper shows that LSTMs can be competitive at scale. While limitations exist in terms of parallelization and hyperparameter tuning, the research shows promising potential for further development. The authors posit further research and improvements could allow xLSTM to reach its full potential.
My Thoughts
- How does the constant error carousel mitigate the vanishing gradient problem in the LSTM?
- The constant error carousel is a way to keep the error constant over time. This helps to prevent the vanishing gradient problem in the LSTM.
- How are the gates in the original LSTM binary?
- Sigmoid, saturation and a threshold at 0.5
- What is the long term memory in the LSTM?
- the cell state c_{t-1}
- What is the short term memory in the LSTM?
- the hidden state h_{t-1}
- How far do we get in language modeling when scaling LSTMs to billions of parameters, leveraging the latest techniques from modern LLMs, but mitigating known limitations of LSTMs
Binary nature of non exponential Gating Mechanisms
If we try to understand why are the gating mechanisms in the original LSTM is described here as binary?
It helps to the properties of the sigmoid functions that are explained in Video 4.
Supplementary Figure 1 shows that The sigmoid function has a domain of \mathbb{R} and a range of (0,1). This means that the sigmoid function can only output values between 0 and 1.
It has a very sharp gradient around 0 if the bias is set to 0. This means that the sigmoid function acts as a binary function around 0.
The Sigmoid function tends to saturate. Now sigmoid function around 0 isn’t quite quite binary but outside of (-6,+6) it becomes saturated and acts very much as a binary function.
If we use it as a loss function or a decision function, the sigmoid function is used with a threshold of 0.5. This means that if the output of the sigmoid function is greater than 0.5, the decision is 1, and if it is less than 0.5, the decision is 0. That is how the sigmoid function can become binary.
Note that we can use thresholding during inference to make the decision binary and we can keep them as continuous values during training so we can have a smooth gradient for back-propagation.
Even without thresholding the sigmoid function can become binary this is due to the saturation of the sigmoid function. I recall that Hinton in his Coursera course on Neural Networks and Deep Learning mentioned that activation function that become saturated are problematic. I can say that at last I think I understand what he meant:
I see that that sigmoid functions can fall off the manifold of the data and this can be a problem. This is why the ReLU function is used in the Gated Recurrent Unit (GRU) and the Transformer. Falling off the manifold of the data means that the sigmoid function becomes saturated (above 6 and below -6). At this point the back-propagation steps are no longer able to change the weight or bias since the gradient is effectively so learning stops.
This becomes a is a problem in two senses. The sigmoid unit is likely to be stuck in a setting that only representative of part of the training data. The rest of the network which is not stuck now has to learn to compensate for this.
This issues may well be the root cause LSTM limitation number 1 - the inability to revise storage decisions. It seems that the authors decided to use the exponential gating function to address this issues.
This is why the gating mechanisms in the original LSTM are binary. The sigmoid function is used to control the flow of information in the LSTM by deciding which information to keep and which to discard. The sigmoid function is used to decide how much of the new input information should be added to the cell state and how much of the old cell state should be retained. This binary nature of the sigmoid function is what allows the LSTM to control the flow of information and decide what to remember and what to forget.
The Paper
References
The paper on open review has some additional insights from the authors
XLSTM — Extended Long Short-Term Memory Networks By Shrinivasan Sankar — May 20, 2024
References
Citation
@online{bochman2025,
author = {Bochman, Oren},
title = {xLSTM: {Extended} {Long} {Short-Term} {Memory}},
date = {2025-02-03},
url = {https://orenbochman.github.io/notes-nlp/reviews/paper/2025-xLSTM/},
langid = {en}
}