My notes for Week 1 of the Natural Language Processing with Probabilistic Models Course in the Natural Language Processing Specialization Offered by DeepLearning.AI on Coursera
- Word probabilities
- Dynamic programming
- Minimum edit distance
- Autocorrect
Overview
We use auto-correct everyday. When we send your friend a text message, or when we make a mistake in a query, there is an autocorrect behind the scenes that corrects the sentence for you. This week we are also going to learn about minimum edit distance, which tells we the minimum amount of edits to change one word into another. In doing that, we will learn about dynamic programming which is an important programming concept which frequently comes up in interviews and could be used to solve a lot of optimization problems.
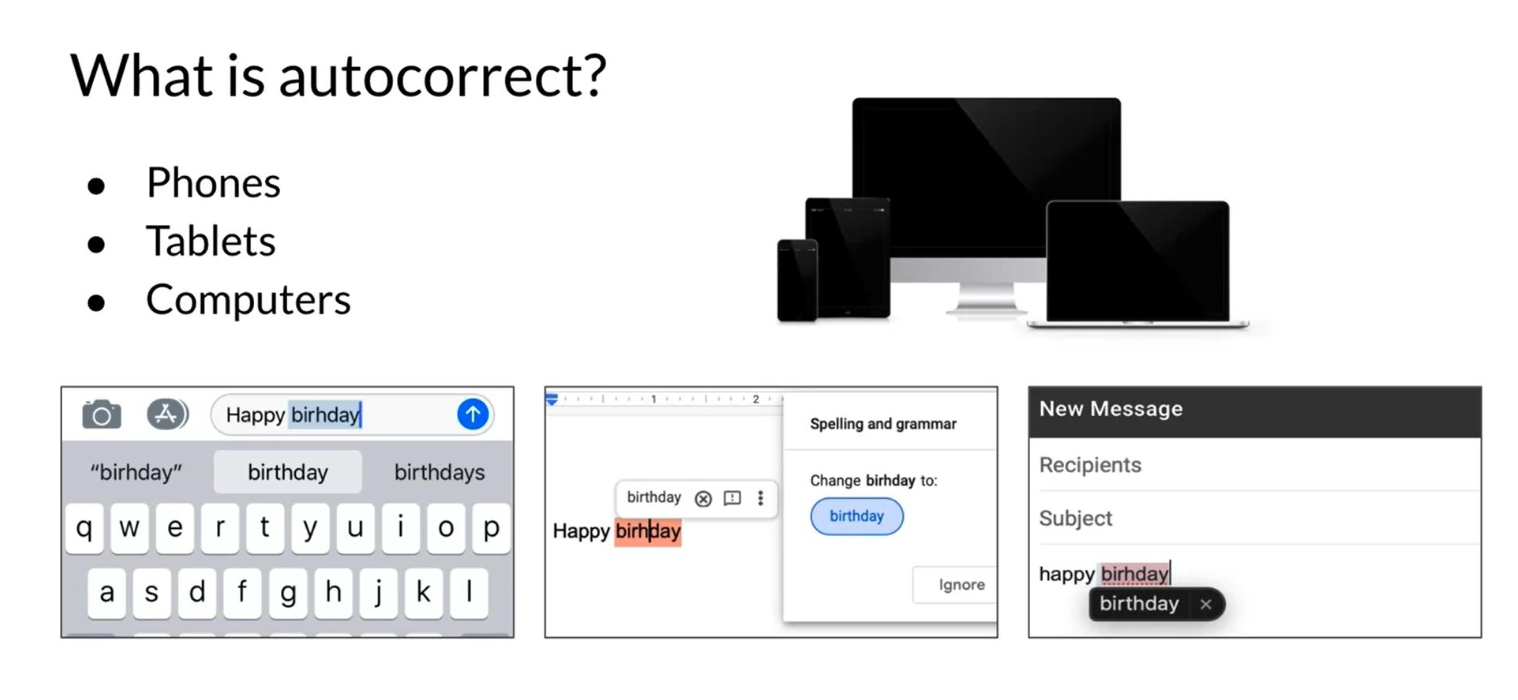
Autocorrect
Autocorrects are used everywhere. We use them in your phones, tablets, and computers.
To implement autocorrect in this week’s assignment, we have to follow these steps:
- Identify a misspelled word
- Find strings n edit distance away: (these could be random strings)
- Filter candidates: (keep only the real words from the previous steps)
- Calculate word probabilities: (choose the word that is most likely to occur in that context)
Building the model:
- Identify the misspelled word
- When identifying the misspelled word, we can check whether it is in the vocabulary. If we don’t find it, then it is probably a typo.
- Find strings n edit distance away
- Filter candidates
- In this step, we want to take all the words generated above and then only keep the actual words that make sense and that we can find in your vocabulary.
Lab: Building the vocabulary
Building the model II
- Calculating word probabilities
Note that we are storing the count of words and then we can use that to generate the probabilities. For this week, we will be counting the probabilities of words occurring. If we want to build a slightly more sophisticated auto-correct we can keep track of two words occurring next to each other instead. We can then use the previous word to decide. For example which combo is more likely, there friend or their friend? For this week however we will be implementing the probabilities by just using the word frequencies.
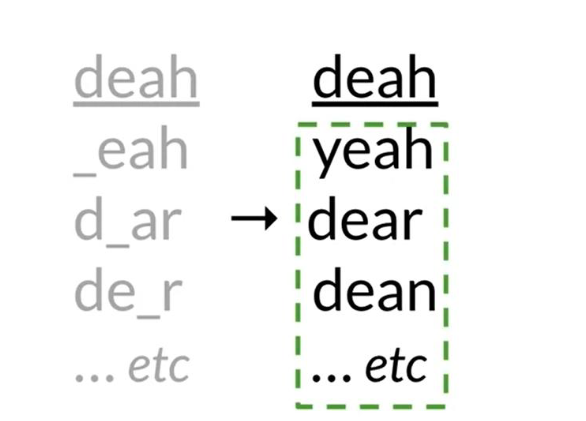
Here is a summary of everything we have seen before in the previous two videos.
Lab: Candidates from Edits
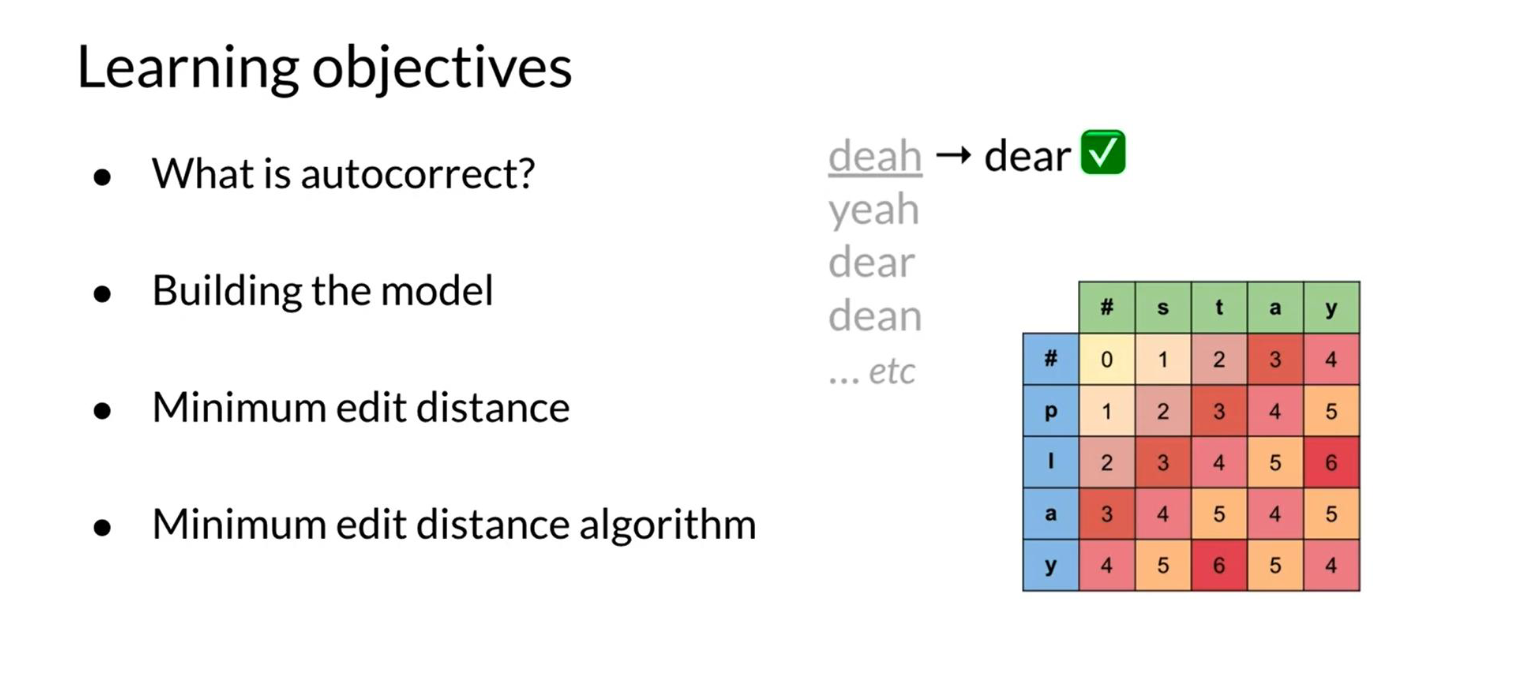
Minimum edit distance
Minimum edit distance allows we to:
- Evaluate similarity between two strings
- Find the minimum number of edits between two strings
- Implement spelling correction, document similarity, machine translation, DNA sequencing, and more
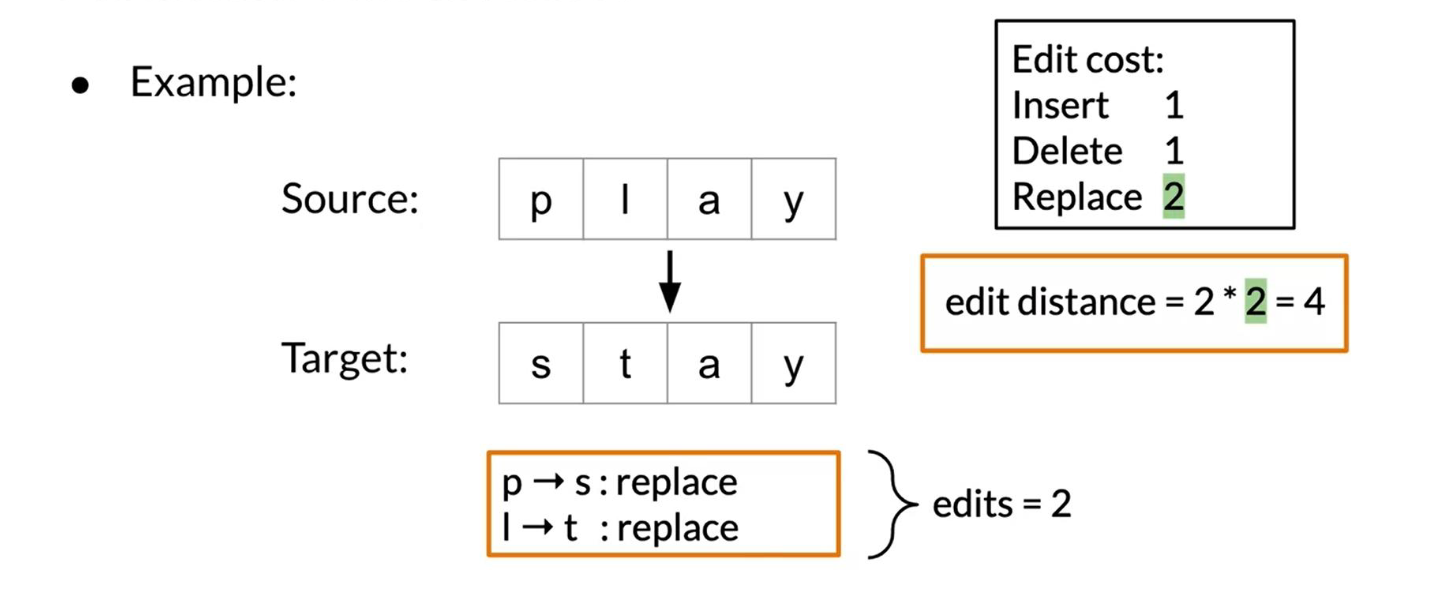
Remember that the edits include:
- Insert (add a letter) ‘to’: ‘top’, ‘two’ …
- Delete (remove a letter) ‘hat’: ‘ha’, ‘at’, ‘ht’
- Replace (change 1 letter to another) ‘jaw’: ‘jar’, ‘paw’, …
Here is a concrete example where we calculate the cost (i.e. edit distance) between two strings.
Note that as your strings get larger it gets much harder to calculate the minimum edit distance. Hence we will now learn about the minimum edit distance algorithm!
Minimum edit distance algorithm
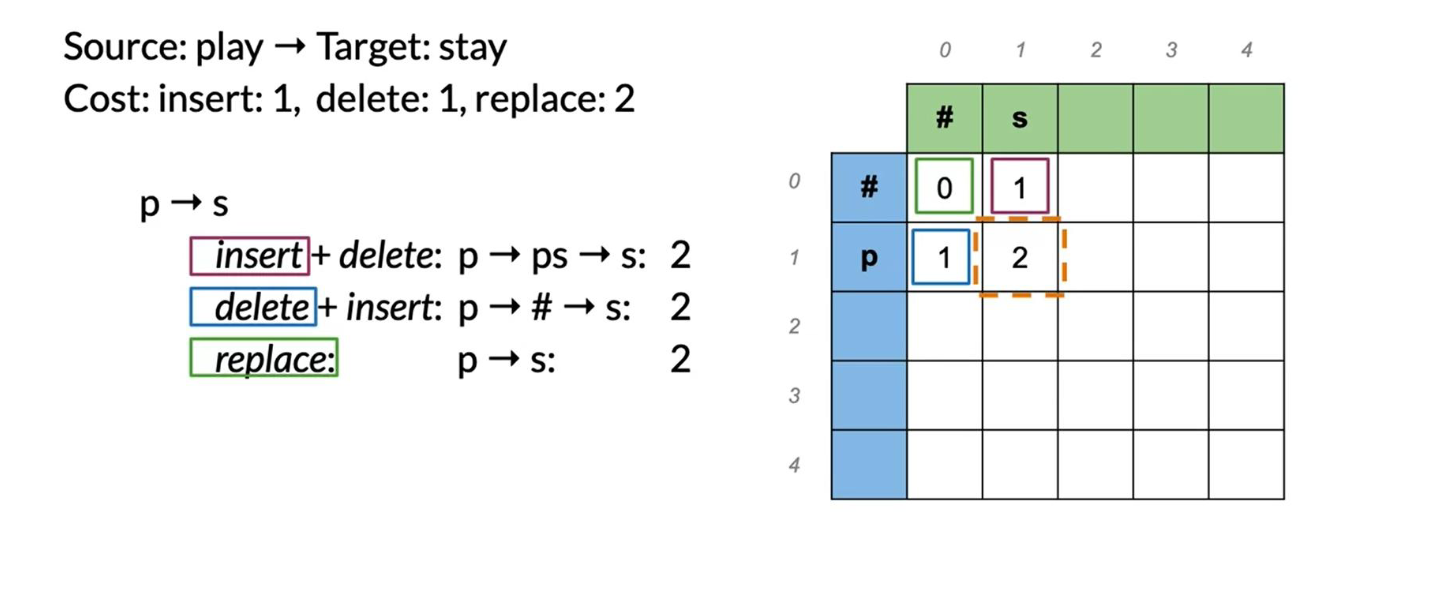
When computing the minimum edit distance, we would start with a source word and transform it into the target word. Let’s look at the following example:
To go:
- from # → # has a cost of 0
- from p → # has a cost of 1, because that is the cost of a delete.
- from p → s has a cost of 2, delete p and insert s.
We can keep going this way by populating one element at a time, but it turns out there is a faster way to do this.
Wee will learn about it next.
Minimum edit distance algorithm II
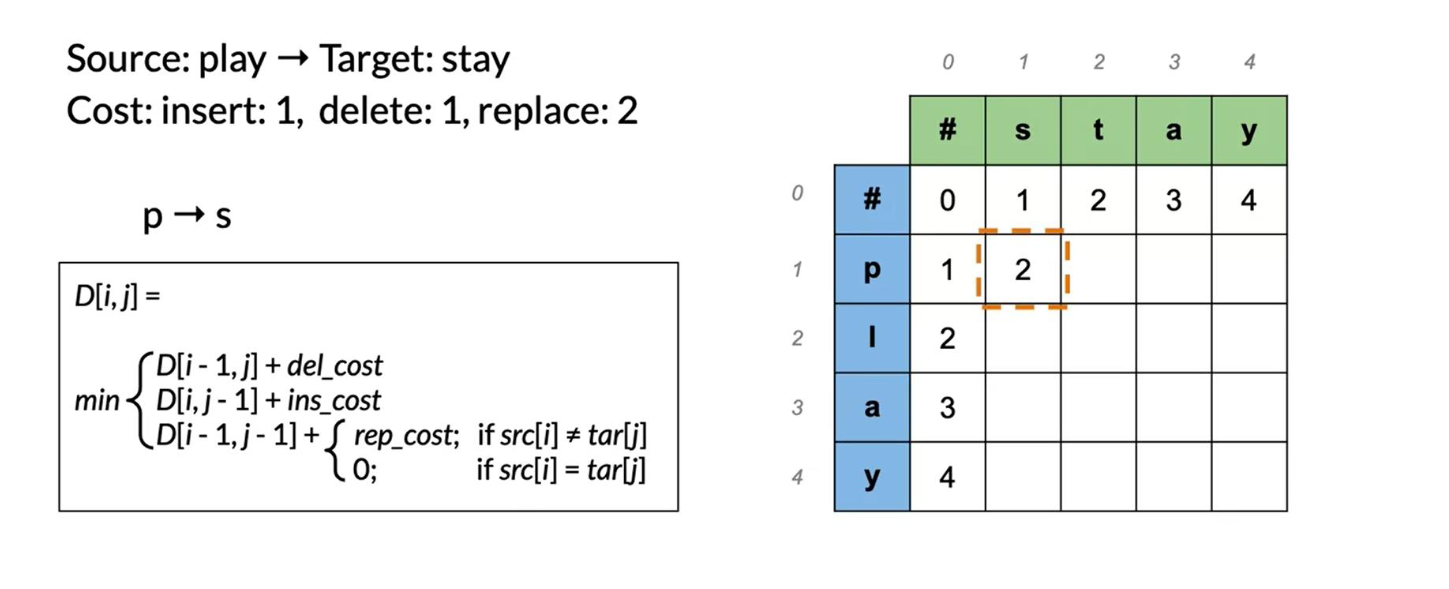
To populate the following table:
There are three equations:
D[i,j] = D[i-1, j] + del_cost: this indicates we want to populate the current cell (i,j) by using the cost in the cell found directly above.
D[i,j] = D[i, j-1] + ins_cost: this indicates we want to populate the current cell (i,j) by using the cost in the cell found directly to its left.
D[i,j] = D[i-1, j-1] + rep_cost: the rep cost can be 2 or 0 depending if we are going to actually replace it or not.
At every time step we check the three possible paths where we can come from and we select the least expensive one. Once we are done, we get the following:
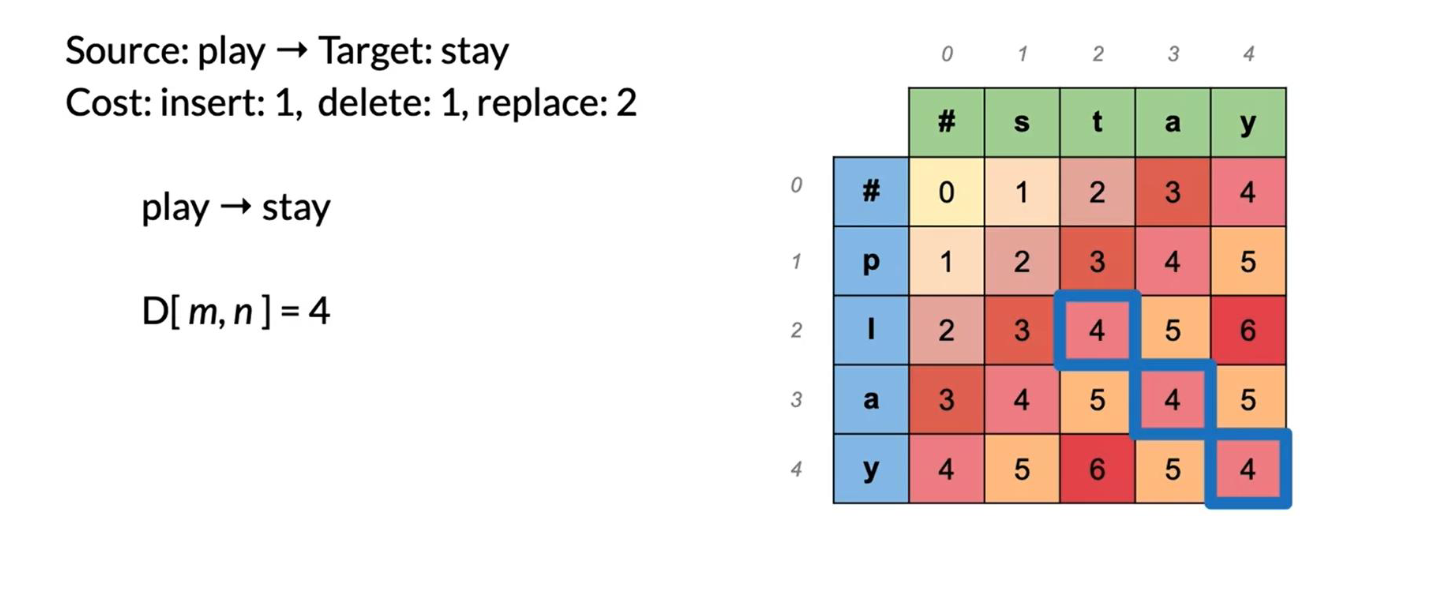
Minimum edit distance III
To summarize, we have seen the levenshtein distance which specifies the cost per operation. If we need to reconstruct the path of how we got from one string to the other, we can use a backtrace. We should keep a simple pointer in each cell letting we know where we came from to get there. So we know the path taken across the table from the top left corner, to the bottom right corner. We can then reconstruct it.
This method for computation instead of brute force is a technique known as dynamic programming. We first solve the smallest subproblem first and then reusing that result we solve the next biggest subproblem, saving that result, reusing it again, and so on. This is exactly what we did by populating each cell from the top right to the bottom left. It’s a well-known technique in computer science!
Citation
@online{bochman2020,
author = {Bochman, Oren},
title = {Autocorrect and Minimum Edit Distance},
date = {2020-10-15},
url = {https://orenbochman.github.io/notes-nlp/notes/c2w1/},
langid = {en}
}