Chapter 11: Survival Analysis - Lab Part 1

Survival Analysis

• In this lab, we perform survival analyses on three separate data sets. In Section 1.1 we analyze the BrainCancer data that was first described in Section~.
• In part 2, we examine the Publication data from Section~.
• Finally, in part 3 we explore a simulated call-center data set.

We begin by importing some of our libraries at this top level. This makes the code more readable, as scanning the first few lines of the notebook tell us what libraries are used in this notebook.

from matplotlib.pyplot import subplots
import numpy as np
import pandas as pd
from ISLP.models import ModelSpec as MS
from ISLP import load_data

We also collect the new imports needed for this lab.

from lifelines import KaplanMeierFitter, CoxPHFitter
from lifelines.statistics import logrank_test, multivariate_logrank_test
from ISLP.survival import sim_time

km = KaplanMeierFitter()
coxph = CoxPHFitter

Brain Cancer Data

We begin with the BrainCancer data set, contained in the ISLP package.

BrainCancer = load_data('BrainCancer')
BrainCancer.columns

Index(['sex', 'diagnosis', 'loc', 'ki', 'gtv', 'stereo', 'status', 'time'], dtype='object')

The rows index the 88 patients, while the 8 columns contain the predictors and outcome variables. We first briefly examine the data.

BrainCancer['sex'].value_counts()

sex
Female    45
Male      43
Name: count, dtype: int64

BrainCancer['diagnosis'].value_counts()

diagnosis
Meningioma    42
HG glioma     22
Other         14
LG glioma      9
Name: count, dtype: int64

BrainCancer['status'].value_counts()

status
0    53
1    35
Name: count, dtype: int64

Before beginning an analysis, it is important to know how the status variable has been coded. Most software uses the convention that a status of 1 indicates an uncensored observation (often death), and a status of 0 indicates a censored observation. But some scientists might use the opposite coding. For the BrainCancer data set 35 patients died before the end of the study, so we are using the conventional coding.

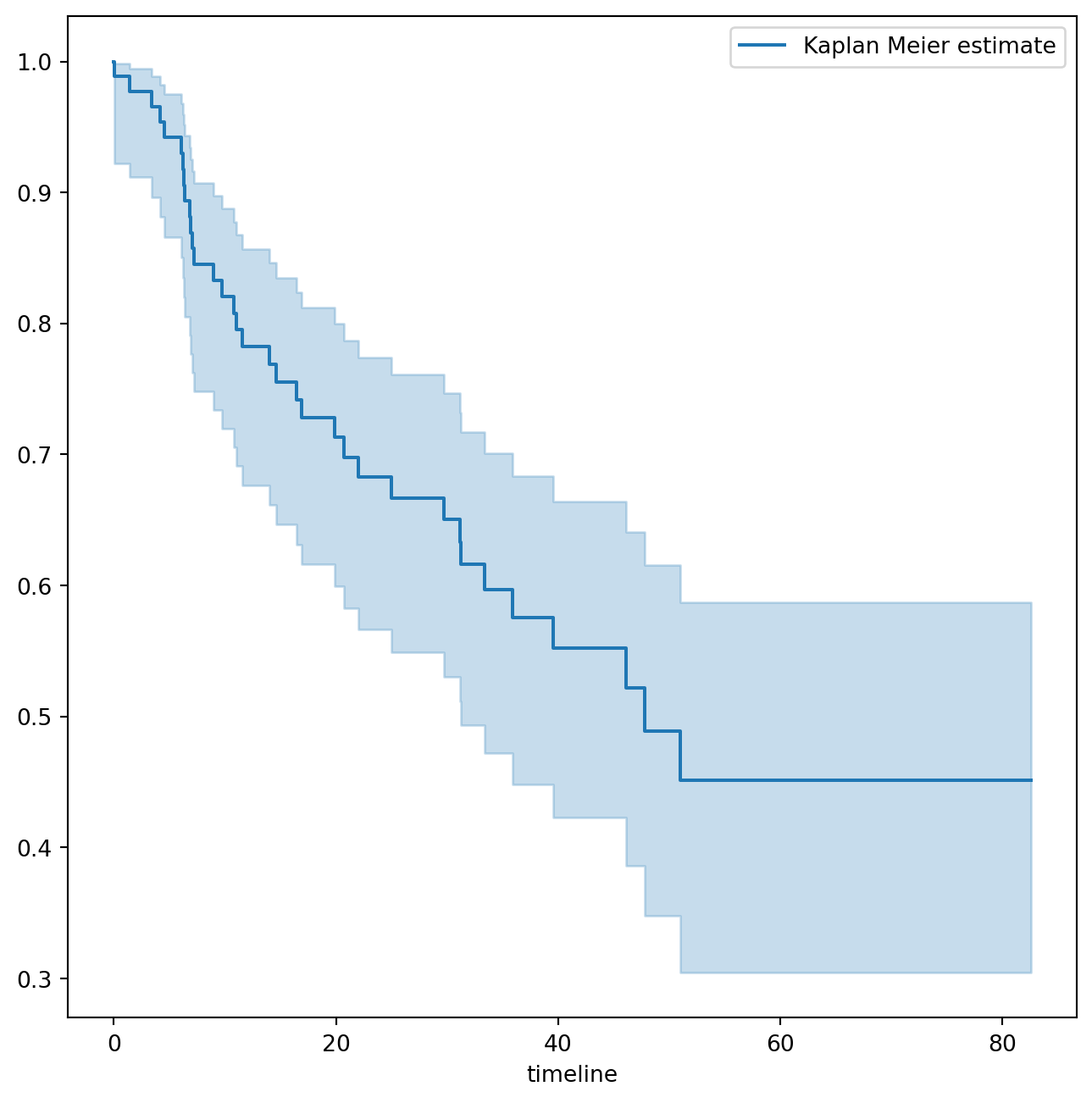
To begin the analysis, we re-create the Kaplan-Meier survival curve shown in Figure~. The main package we will use for survival analysis is lifelines. The variable time corresponds to y_i, the time to the ith event (either censoring or death). The first argument to km.fit is the event time, and the second argument is the censoring variable, with a 1 indicating an observed failure time. The plot() method produces a survival curve with pointwise confidence intervals. By default, these are 90% confidence intervals, but this can be changed by setting the alpha argument to one minus the desired confidence level.

fig, ax = subplots(figsize=(8,8))
km = KaplanMeierFitter()
km_brain = km.fit(BrainCancer['time'], BrainCancer['status'])
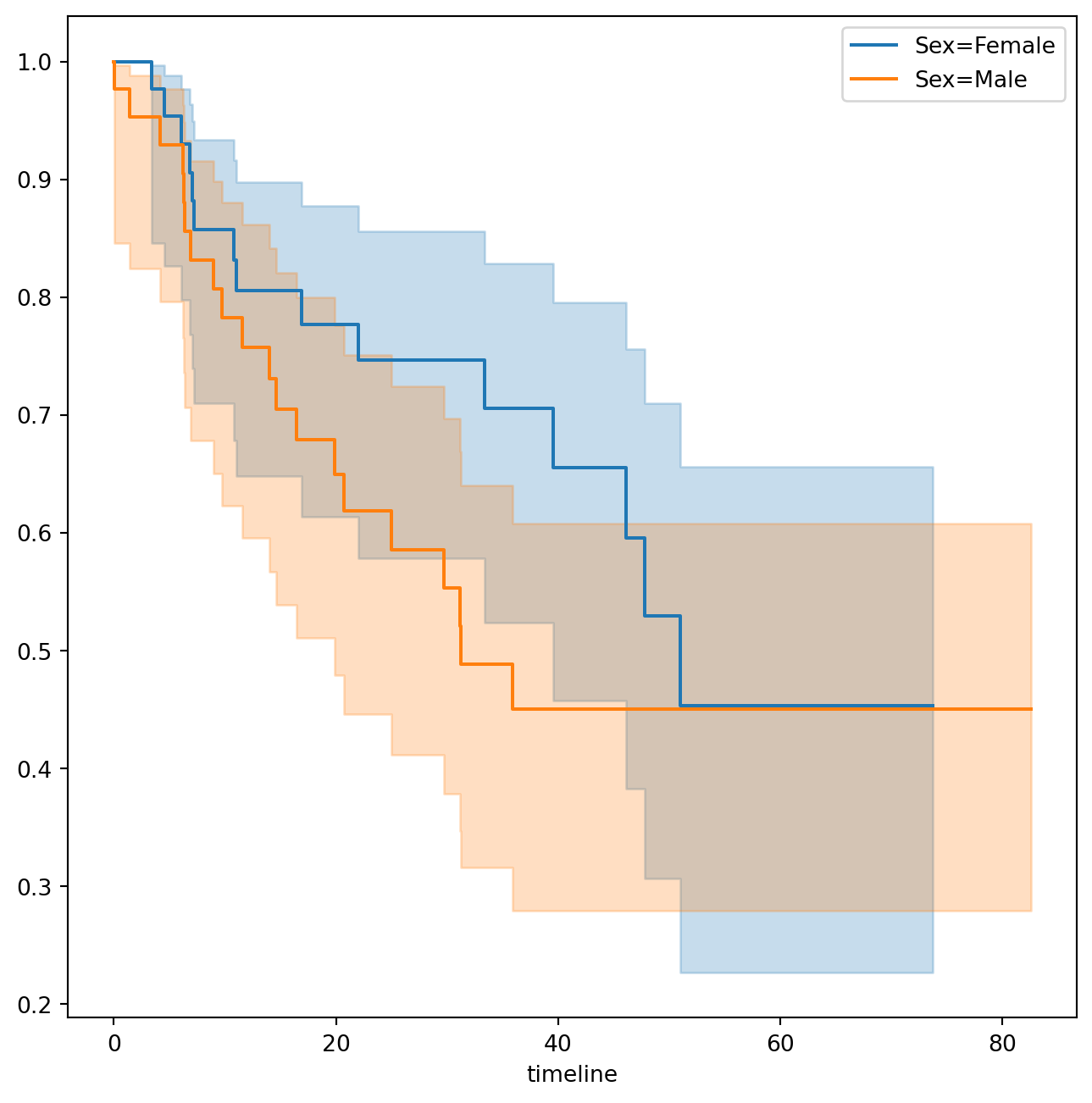
km_brain.plot(label='Kaplan Meier estimate', ax=ax)

Next we create Kaplan-Meier survival curves that are stratified by sex, in order to reproduce Figure~. We do this using the groupby() method of a dataframe. This method returns a generator that can be iterated over in the for loop. In this case, the items in the for loop are 2-tuples representing the groups: the first entry is the value of the grouping column sex while the second value is the dataframe consisting of all rows in the dataframe matching that value of sex. We will want to use this data below in the log-rank test, hence we store this information in the dictionary by_sex. Finally, we have also used the notion of string interpolation to automatically label the different lines in the plot. String interpolation is a powerful technique to format strings — Python has many ways to facilitate such operations.

fig, ax = subplots(figsize=(8,8))
by_sex = {}
for sex, df in BrainCancer.groupby('sex'):
    by_sex[sex] = df
    km_sex = km.fit(df['time'], df['status'])
    km_sex.plot(label='Sex=%s' % sex, ax=ax)

/tmp/ipykernel_1616988/3279415391.py:3: FutureWarning: The default of observed=False is deprecated and will be changed to True in a future version of pandas. Pass observed=False to retain current behavior or observed=True to adopt the future default and silence this warning.
  for sex, df in BrainCancer.groupby('sex'):

As discussed in Section~, we can perform a log-rank test to compare the survival of males to females. We use the logrank_test() function from the lifelines.statistics module. The first two arguments are the event times, with the second denoting the corresponding (optional) censoring indicators.

logrank_test(by_sex['Male']['time'],
             by_sex['Female']['time'],
             by_sex['Male']['status'],
             by_sex['Female']['status'])

t_0	-1
null_distribution	chi squared
degrees_of_freedom	1
test_name	logrank_test

	test_statistic	p	-log2(p)
0	1.44	0.23	2.12

The resulting p-value is 0.23, indicating no evidence of a difference in survival between the two sexes.

Next, we use the CoxPHFitter() estimator from lifelines to fit Cox proportional hazards models. To begin, we consider a model that uses sex as the only predictor.

coxph = CoxPHFitter # shorthand
sex_df = BrainCancer[['time', 'status', 'sex']]
model_df = MS(['time', 'status', 'sex'],
              intercept=False).fit_transform(sex_df)
cox_fit = coxph().fit(model_df,
                      'time',
                      'status')
cox_fit.summary[['coef', 'se(coef)', 'p']]

	coef	se(coef)	p
covariate
sex[Male]	0.407668	0.342004	0.233262

The first argument to fit should be a data frame containing at least the event time (the second argument time in this case), as well as an optional censoring variable (the argument status in this case). Note also that the Cox model does not include an intercept, which is why we used the intercept=False argument to ModelSpec above. The summary() method delivers many columns; we chose to abbreviate its output here. It is possible to obtain the likelihood ratio test comparing this model to the one with no features as follows:

cox_fit.log_likelihood_ratio_test()

null_distribution	chi squared
degrees_freedom	1
test_name	log-likelihood ratio test

	test_statistic	p	-log2(p)
0	1.44	0.23	2.12

Regardless of which test we use, we see that there is no clear evidence for a difference in survival between males and females. As we learned in this chapter, the score test from the Cox model is exactly equal to the log rank test statistic!

Now we fit a model that makes use of additional predictors. We first note that one of our diagnosis values is missing, hence we drop that observation before continuing.

cleaned = BrainCancer.dropna()
all_MS = MS(cleaned.columns, intercept=False)
all_df = all_MS.fit_transform(cleaned)
fit_all = coxph().fit(all_df,
                      'time',
                      'status')
fit_all.summary[['coef', 'se(coef)', 'p']]

	coef	se(coef)	p
covariate
sex[Male]	0.183748	0.360358	0.610119
diagnosis[LG glioma]	-1.239530	0.579555	0.032455
diagnosis[Meningioma]	-2.154566	0.450524	0.000002
diagnosis[Other]	-1.268870	0.617672	0.039949
loc[Supratentorial]	0.441195	0.703669	0.530665
ki	-0.054955	0.018314	0.002693
gtv	0.034293	0.022333	0.124661
stereo[SRT]	0.177778	0.601578	0.767597

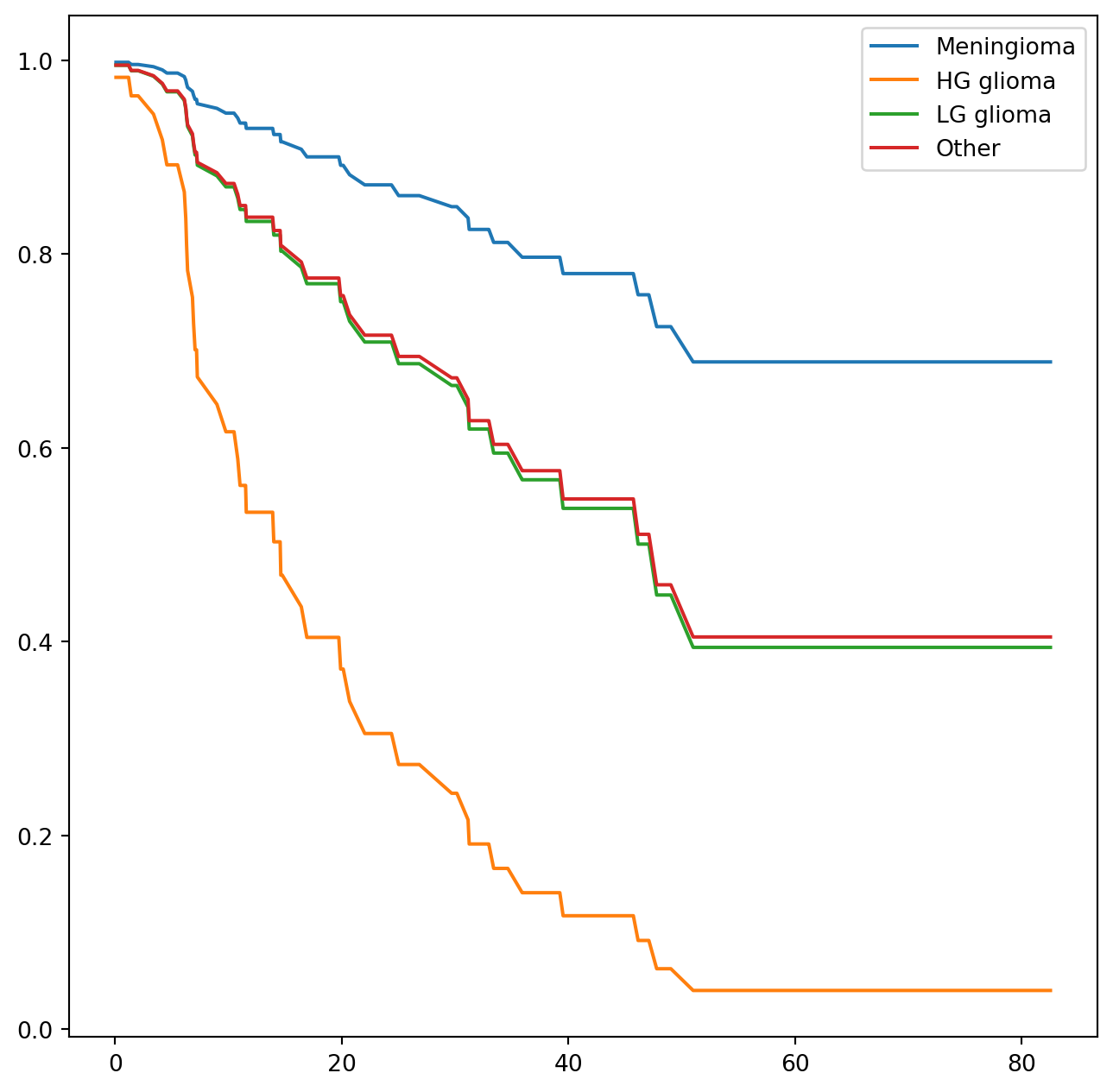
The diagnosis variable has been coded so that the baseline corresponds to HG glioma. The results indicate that the risk associated with HG glioma is more than eight times (i.e. e^{2.15}=8.62) the risk associated with meningioma. In other words, after adjusting for the other predictors, patients with HG glioma have much worse survival compared to those with meningioma. In addition, larger values of the Karnofsky index, ki, are associated with lower risk, i.e. longer survival.

Finally, we plot estimated survival curves for each diagnosis category, adjusting for the other predictors. To make these plots, we set the values of the other predictors equal to the mean for quantitative variables and equal to the mode for categorical. To do this, we use the apply() method across rows (i.e. axis=0) with a function representative that checks if a column is categorical or not.

levels = cleaned['diagnosis'].unique()
def representative(series):
    if hasattr(series.dtype, 'categories'):
        return pd.Series.mode(series)
    else:
        return series.mean()
modal_data = cleaned.apply(representative, axis=0)

We make four copies of the column means and assign the diagnosis column to be the four different diagnoses.

modal_df = pd.DataFrame(
              [modal_data.iloc[0] for _ in range(len(levels))])
modal_df['diagnosis'] = levels
modal_df

	sex	diagnosis	loc	ki	gtv	stereo	status	time
0	Female	Meningioma	Supratentorial	80.91954	8.687011	SRT	0.402299	27.188621
0	Female	HG glioma	Supratentorial	80.91954	8.687011	SRT	0.402299	27.188621
0	Female	LG glioma	Supratentorial	80.91954	8.687011	SRT	0.402299	27.188621
0	Female	Other	Supratentorial	80.91954	8.687011	SRT	0.402299	27.188621

We then construct the model matrix based on the model specification all_MS used to fit the model, and name the rows according to the levels of diagnosis.

modal_X = all_MS.transform(modal_df)
modal_X.index = levels
modal_X

	sex[Male]	diagnosis[LG glioma]	diagnosis[Meningioma]	diagnosis[Other]	loc[Supratentorial]	ki	gtv	stereo[SRT]	status	time
Meningioma	0.0	0.0	1.0	0.0	1.0	80.91954	8.687011	1.0	0.402299	27.188621
HG glioma	0.0	0.0	0.0	0.0	1.0	80.91954	8.687011	1.0	0.402299	27.188621
LG glioma	0.0	1.0	0.0	0.0	1.0	80.91954	8.687011	1.0	0.402299	27.188621
Other	0.0	0.0	0.0	1.0	1.0	80.91954	8.687011	1.0	0.402299	27.188621

We can use the predict_survival_function() method to obtain the estimated survival function.

predicted_survival = fit_all.predict_survival_function(modal_X)
predicted_survival

	Meningioma	HG glioma	LG glioma	Other
0.07	0.997947	0.982430	0.994881	0.995029
1.18	0.997947	0.982430	0.994881	0.995029
1.41	0.995679	0.963342	0.989245	0.989555
1.54	0.995679	0.963342	0.989245	0.989555
2.03	0.995679	0.963342	0.989245	0.989555
...	...	...	...	...
65.02	0.688772	0.040136	0.394181	0.404936
67.38	0.688772	0.040136	0.394181	0.404936
73.74	0.688772	0.040136	0.394181	0.404936
78.75	0.688772	0.040136	0.394181	0.404936
82.56	0.688772	0.040136	0.394181	0.404936

85 rows × 4 columns

This returns a data frame, whose plot methods yields the different survival curves. To avoid clutter in the plots, we do not display confidence intervals.

fig, ax = subplots(figsize=(8, 8))
predicted_survival.plot(ax=ax);