Better SPLOM

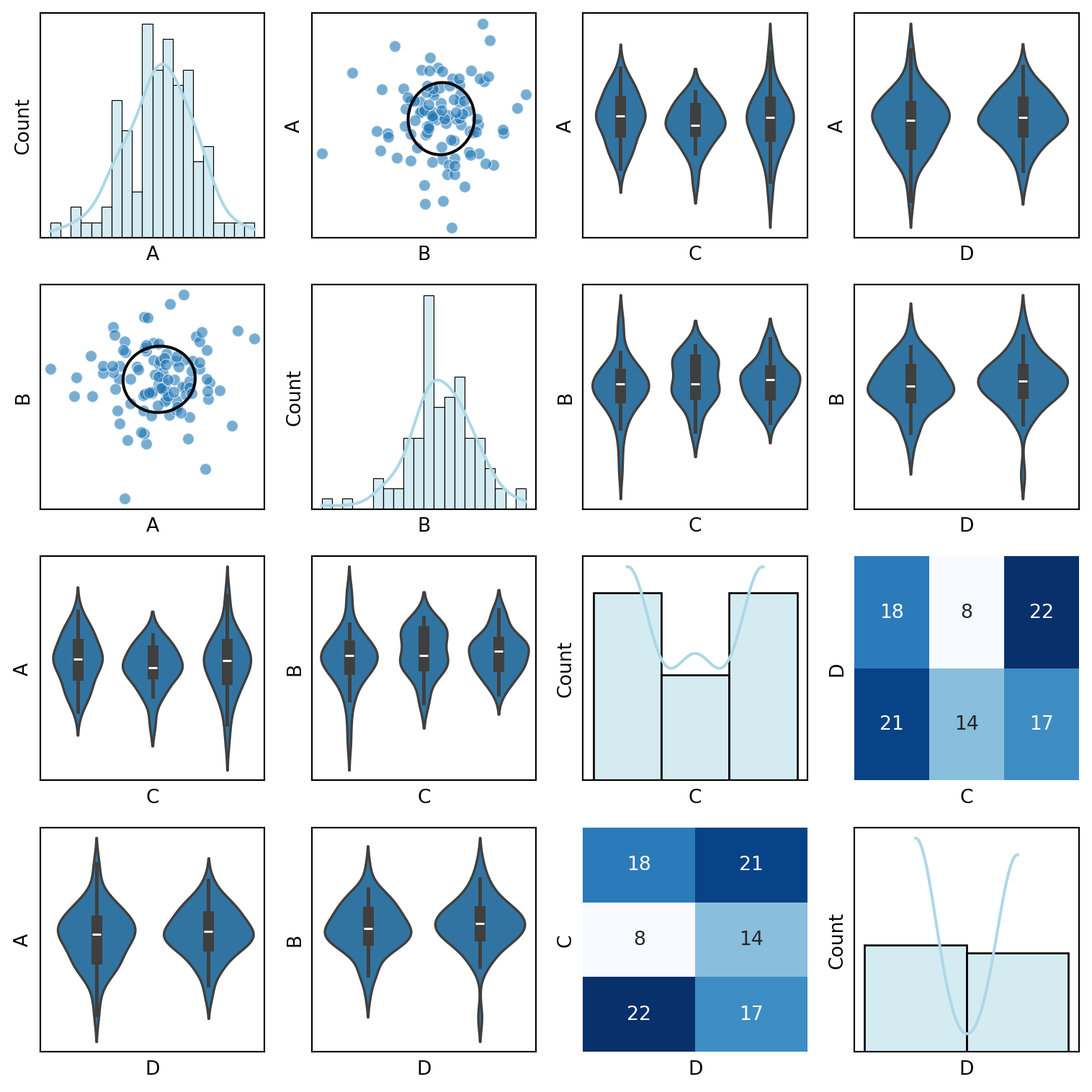
In the notes on I had some ideas about making a better SPLOMs. A splom is a scatterplot matrix.

The first batch of ideas involve making scatterplot more infomative by pickinga more suitable plot type based on the data types of the variables being plotted.

1. for a continuous vs continuous variable pairs plot a scatter plot.
2. for a continuous vs discrete variable pairs plot a violin plot.
3. for a discrete vs discrete variable pairs plot a heatmap.
4. on the diagonal plot histograms with a density plot overlay.
5. for the lower triangle of the plot, plot correlation ellipses. And the correlation ellipses can be overlayed with a number for the correlation coefficient.

The second batch of ideas involve making the plot more useful for understanding effects in the data and potential regression issues like outliers and high leverage points, heteroscedasticity, and non-linear relationships. And one more issue that I came across is how to handle zero inflation arising from one or the other variable….

Another thought about SPLOM is to make the cells of the plot three dimensional so we could see the two predictors vs the response variable when we move off the first collumn.

6. Highlight effects in these plots. using a regression line or a loess line for the main effects.
7. For the second order effects, we might show the fit a 3d quadratic spline or loess for the two predictors as a surface in a 3d plot. If we were interactive we might also show
   • The residuals
   • Error surfaces above and below the fit surface. A sort of confidence interval for the fit
   • The outliers and high leverage points for the interaction terms. Perhaps as bubbles for the residuals and as points for the outliers and high leverage points.
   • The zero inflation points. Perhaps as a different color for the residuals.
8. highlight hetroscedasticity by a residual from a normal distribution….
9. make the
10. make it interactive.

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from sklearn.preprocessing import LabelEncoder

def correlation_ellipse(ax, x, y, data, **kwargs):
    """Plot correlation ellipses like R's circles package."""
    cov = np.cov(data[x], data[y])
    eigvals, eigvecs = np.linalg.eig(cov)
    
    angle = np.degrees(np.arctan2(*eigvecs[:, 0][::-1]))
    
    ellipse = Ellipse(
        xy=(data[x].mean(), data[y].mean()),
        width=2 * np.sqrt(eigvals[0]),
        height=2 * np.sqrt(eigvals[1]),
        angle=angle,
        edgecolor='black',
        facecolor='none',
        linewidth=1.5
    )
    ax.add_patch(ellipse)

def custom_pair_plot(df):
    """Generate a pair plot with scatter plots for continuous variables,
    violin plots for discrete variables, and correlation ellipses."""
    continuous_vars = df.select_dtypes(include=['float64', 'int64']).columns
    discrete_vars = df.select_dtypes(include=['object', 'category']).columns

    label_encoders = {col: LabelEncoder().fit(df[col]) for col in discrete_vars}
    df_encoded = df.copy()
    
    # Encode categorical variables
    for col in discrete_vars:
        df_encoded[col] = label_encoders[col].transform(df[col])

    num_vars = df_encoded.shape[1]
    fig, axes = plt.subplots(num_vars, num_vars, figsize=(2*num_vars, 2*num_vars))
    
    for i, var1 in enumerate(df_encoded.columns):
        for j, var2 in enumerate(df_encoded.columns):
            ax = axes[i, j]
            if i == j:
                sns.histplot(df[var1], ax=ax, kde=True, bins=20, color="lightblue")
            elif var1 in continuous_vars and var2 in continuous_vars:
                sns.scatterplot(x=df[var2], y=df[var1], ax=ax, alpha=0.6)
                correlation_ellipse(ax, var2, var1, df_encoded)
            elif var1 in discrete_vars and var2 in continuous_vars:
                sns.violinplot(x=df[var1], y=df[var2], ax=ax)
            elif var1 in continuous_vars and var2 in discrete_vars:
                sns.violinplot(x=df[var2], y=df[var1], ax=ax)
            else:
                sns.heatmap(pd.crosstab(df[var2], df[var1]), annot=True, fmt="d", cmap="Blues", ax=ax, cbar=False)

            ax.set_xticks([])
            ax.set_yticks([])

    plt.tight_layout()
    plt.show()

# Example usage
df = pd.DataFrame({
    'A': np.random.randn(100),
    'B': np.random.randn(100) * 2,
    'C': np.random.choice(['Low', 'Medium', 'High'], 100),
    'D': np.random.choice(['Yes', 'No'], 100)
})

custom_pair_plot(df)

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from sklearn.preprocessing import LabelEncoder, MinMaxScaler

def correlation_ellipse(ax, x, y, data, max_size=1.2):
    """Plot a properly scaled correlation ellipse in the lower triangle."""
    x_vals = data[x]
    y_vals = data[y]

    corr = np.corrcoef(x_vals, y_vals)[0, 1]  # Pearson correlation
    cov = np.cov(x_vals, y_vals)
    eigvals, eigvecs = np.linalg.eig(cov)

    # Normalize eigenvalues to ensure uniform ellipse size
    max_eigenvalue = np.max(eigvals)
    width, height = max_size * (eigvals / max_eigenvalue)  # Scale within a fixed box
    angle = np.degrees(np.arctan2(*eigvecs[:, 0][::-1]))

    ellipse = Ellipse(
        xy=(0, 0),  # Centered at (0,0) since we scale manually
        width=width, height=height,
        angle=angle,
        edgecolor='black',
        facecolor='gray',
        alpha=0.3
    )

    ax.add_patch(ellipse)

    # Fix axis limits to keep all ellipses inside a square
    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.set_xticks([])
    ax.set_yticks([])
    ax.set_frame_on(False)  # Remove frame for clarity

def custom_pair_plot(df):
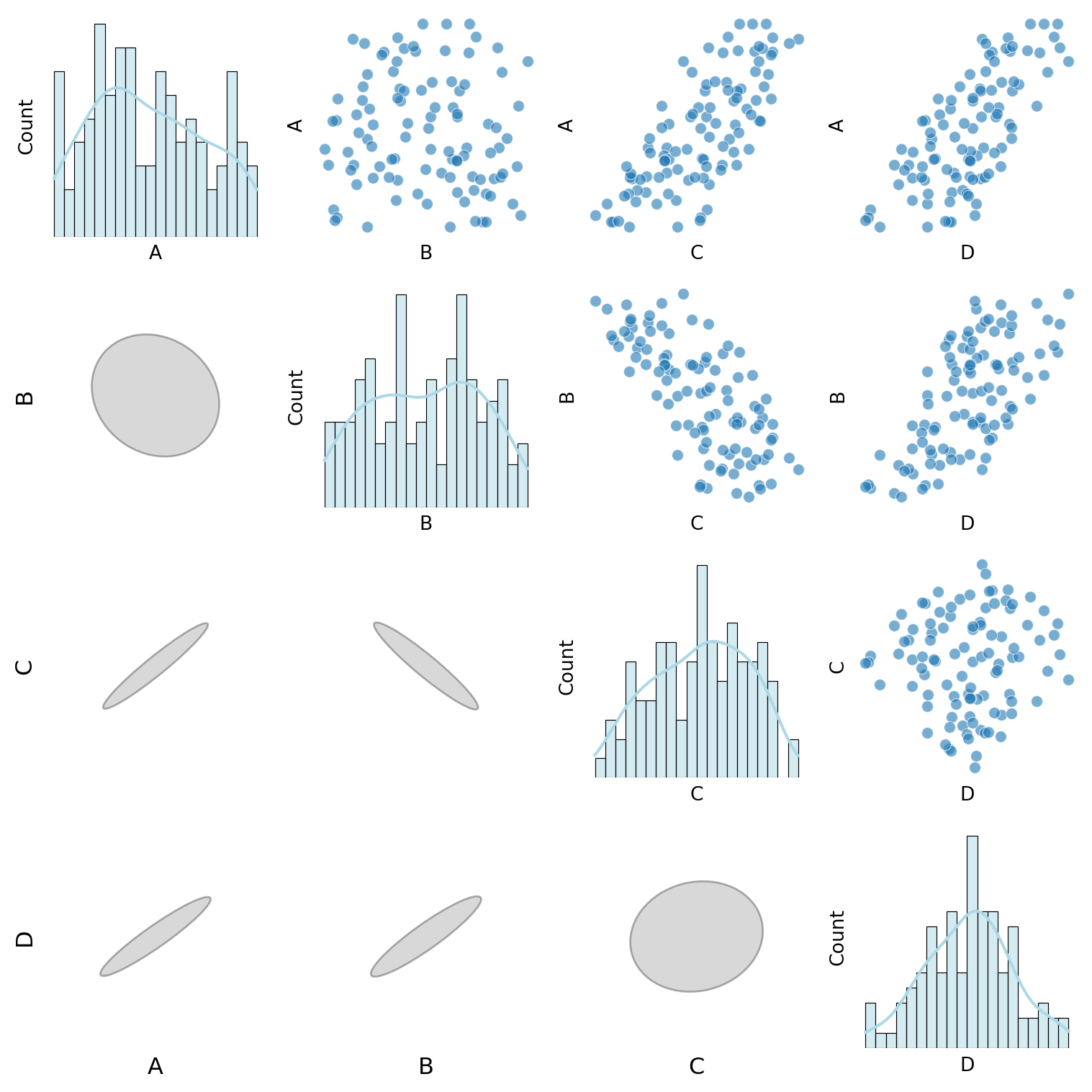
    """Generate a pair plot where:
    - Histograms appear on the diagonal.
    - Scatter & Violin plots are in the upper triangle.
    - Normalized correlation ellipses appear in the lower triangle.
    - Labels for the bottom and left axes of ellipses.
    """
    continuous_vars = df.select_dtypes(include=['float64', 'int64']).columns
    discrete_vars = df.select_dtypes(include=['object', 'category']).columns

    # Normalize all continuous variables to [0,1] for consistent ellipses
    scaler = MinMaxScaler()
    df_encoded = df.copy()
    df_encoded[continuous_vars] = scaler.fit_transform(df[continuous_vars])

    # Encode categorical variables
    label_encoders = {col: LabelEncoder().fit(df[col]) for col in discrete_vars}
    for col in discrete_vars:
        df_encoded[col] = label_encoders[col].transform(df[col])

    num_vars = len(df_encoded.columns)
    fig, axes = plt.subplots(num_vars, num_vars, figsize=(2*num_vars, 2*num_vars))

    for i, var1 in enumerate(df_encoded.columns):
        for j, var2 in enumerate(df_encoded.columns):
            ax = axes[i, j]

            # Diagonal: Histograms
            if i == j:
                sns.histplot(df[var1], ax=ax, kde=True, bins=20, color="lightblue")
            
            # Above diagonal: Scatter & Violin plots
            elif i < j:
                if var1 in continuous_vars and var2 in continuous_vars:
                    sns.scatterplot(x=df[var2], y=df[var1], ax=ax, alpha=0.6)
                elif var1 in discrete_vars and var2 in continuous_vars:
                    sns.violinplot(x=df[var1], y=df[var2], ax=ax)
                elif var1 in continuous_vars and var2 in discrete_vars:
                    sns.violinplot(x=df[var2], y=df[var1], ax=ax)
                else:
                    sns.heatmap(pd.crosstab(df[var2], df[var1]), annot=True, fmt="d", cmap="Blues", ax=ax, cbar=False)

            # Below diagonal: Correlation ellipses
            else:
                correlation_ellipse(ax, var2, var1, df_encoded)

                # Add axis labels for the bottom row and left-most column
                if i == num_vars - 1:
                    ax.set_xlabel(var2, fontsize=12)
                if j == 0:
                    ax.set_ylabel(var1, fontsize=12, rotation=90)

            ax.set_xticks([])
            ax.set_yticks([])
            ax.set_frame_on(False)  # Remove frame for clarity

    plt.tight_layout()
    plt.show()

# Test dataset with very different scales
a = np.random.uniform(size=100)
b = np.random.uniform(size=100)
df = pd.DataFrame({
    'A': (a) * 100.0,
    'B': (b) * 100.0,
    'C': (a - b) - 100.0,    
    'D': (a + b) * 50.0 - 50.0,
})

custom_pair_plot(df)

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

def smart_sns_plot(x, y, data, ax=None, **kwargs):
    """
    Automatically delegates to sns.scatterplot, sns.violinplot, or sns.heatmap 
    based on the data types of x and y.
    
    - Continuous vs. Continuous → sns.scatterplot
    - Continuous vs. Discrete → sns.violinplot
    - Discrete vs. Discrete → sns.heatmap
    """
    if ax is None:
        ax = plt.gca()

    # Determine data types
    x_dtype = data[x].dtype
    y_dtype = data[y].dtype
    is_x_cont = np.issubdtype(x_dtype, np.number)
    is_y_cont = np.issubdtype(y_dtype, np.number)

    if is_x_cont and is_y_cont:
        # Continuous vs. Continuous → Scatter Plot
        sns.scatterplot(x=x, y=y, data=data, ax=ax, **kwargs)
        
    elif is_x_cont and not is_y_cont:
        # Continuous vs. Discrete → Violin Plot
        sns.violinplot(x=y, y=x, data=data, ax=ax, **kwargs)
        
    elif not is_x_cont and is_y_cont:
        # Discrete vs. Continuous → Violin Plot (flipped)
        sns.violinplot(x=x, y=y, data=data, ax=ax, **kwargs)
        
    else:
        # Discrete vs. Discrete → Heatmap
        cross_tab = pd.crosstab(data[x], data[y])
        sns.heatmap(cross_tab, annot=True, fmt="d", cmap="Blues", ax=ax, cbar=False)

    return ax  # Return the modified axis

# Example Usage
df = pd.DataFrame({
    'A': np.random.randn(100),
    'B': np.random.randn(100) * 2,
    'C': np.random.choice(['Low', 'Medium', 'High'], 100),
    'D': np.random.choice(['Yes', 'No'], 100)
})

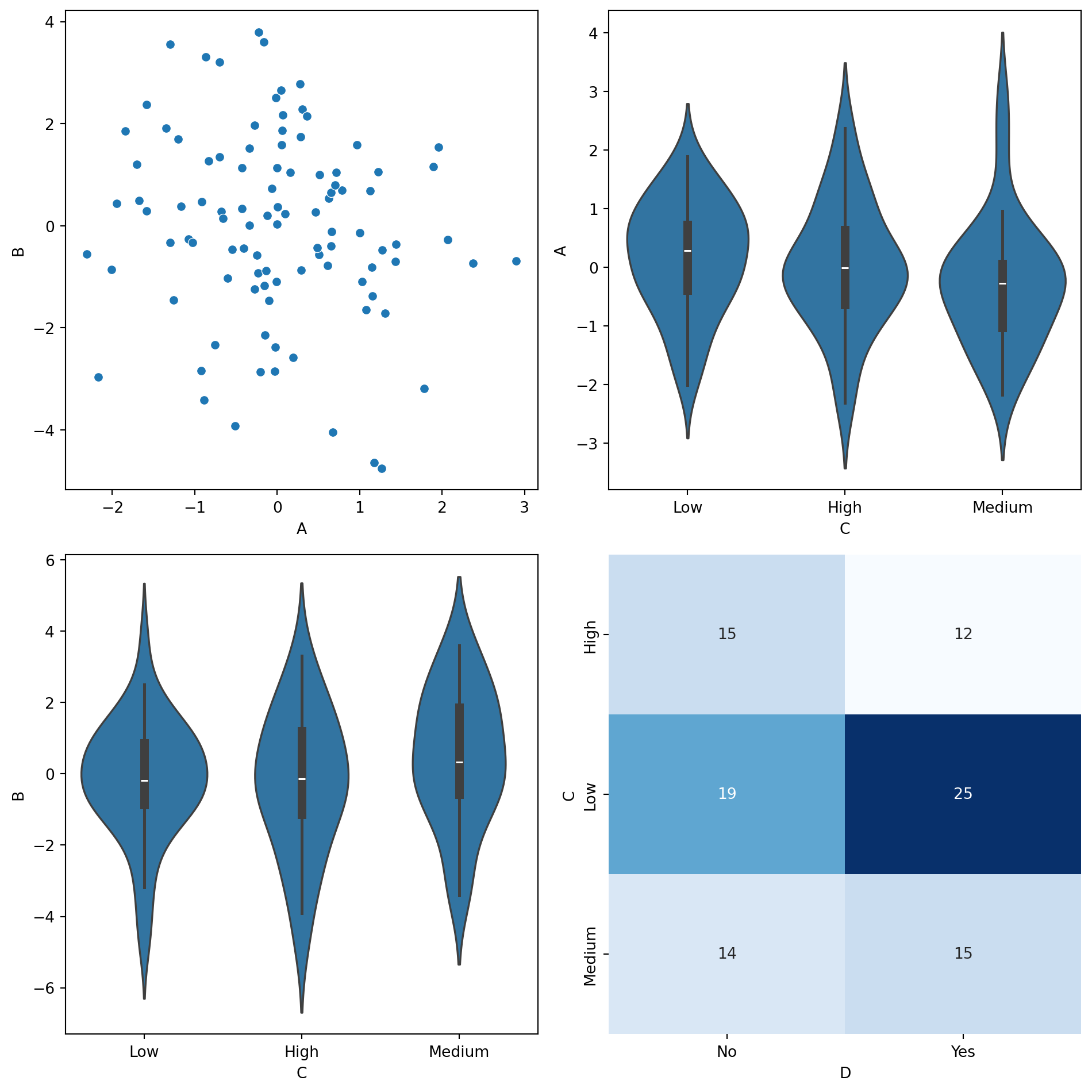
fig, axes = plt.subplots(2, 2, figsize=(10, 10))

# Scatterplot (Continuous vs Continuous)
smart_sns_plot("A", "B", df, ax=axes[0, 0])

# Violinplot (Continuous vs Discrete)
smart_sns_plot("A", "C", df, ax=axes[0, 1])

# Violinplot (Flipped Discrete vs Continuous)
smart_sns_plot("C", "B", df, ax=axes[1, 0])

# Heatmap (Discrete vs Discrete)
smart_sns_plot("C", "D", df, ax=axes[1, 1])

plt.tight_layout()
plt.show()

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from sklearn.preprocessing import MinMaxScaler

def sns_correlation_ellipse(x, y, data, ax=None, max_size=1.2, **kwargs):
    """
    Seaborn-compatible function that plots a correlation ellipse 
    based on the covariance of x and y.

    - Uses eigenvectors/eigenvalues of covariance matrix.
    - Normalizes ellipse size for consistent visuals.
    - Designed for use in sns.pairplot or FacetGrid.
    """
    if ax is None:
        ax = plt.gca()

    # Standardize data for consistent ellipses
    scaler = MinMaxScaler()
    scaled_data = scaler.fit_transform(data[[x, y]])
    x_vals, y_vals = scaled_data[:, 0], scaled_data[:, 1]

    # Compute covariance and eigen decomposition
    cov = np.cov(x_vals, y_vals)
    eigvals, eigvecs = np.linalg.eig(cov)

    # Normalize ellipse size (ensures all ellipses fit in a fixed-size box)
    max_eigenvalue = np.max(eigvals)
    width, height = max_size * (eigvals / max_eigenvalue)
    angle = np.degrees(np.arctan2(*eigvecs[:, 0][::-1]))

    # Draw ellipse at the center
    ellipse = Ellipse(
        xy=(0, 0), width=width, height=height,
        angle=angle, edgecolor="black", facecolor="gray", alpha=0.3
    )
    ax.add_patch(ellipse)

    # Fix axis limits so all ellipses are comparable
    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.set_xticks([])
    ax.set_yticks([])
    ax.set_frame_on(False)

    return ax  # Return modified axis

# Example Data
a = np.random.uniform(size=100)
b = np.random.uniform(size=100)
df = pd.DataFrame({
    'A': (a) * 100.0,
    'B': (b) * 100.0,
    'C': (a - b) - 100.0,    
    'D': (a + b) * 50.0 - 50.0,
})

# Test with individual plots
fig, ax = plt.subplots(figsize=(4, 4))
sns_correlation_ellipse("A", "B", df, ax=ax)
plt.show()

g = sns.pairplot(df, kind="scatter", corner=True)
for i, row_var in enumerate(df.columns):
    for j, col_var in enumerate(df.columns):
        if i > j:  # Only lower triangle
            sns_correlation_ellipse(row_var, col_var, df, ax=g.axes[i, j])
plt.show()

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from sklearn.preprocessing import MinMaxScaler

def sns_correlation_ellipse(x, y, data, ax=None, max_size=1.2, **kwargs):
    """
    Seaborn-compatible function that plots a correlation ellipse 
    based on the covariance of x and y.

    - Uses eigenvectors/eigenvalues of covariance matrix.
    - Normalizes ellipse size for consistent visuals.
    - Designed for use in sns.pairplot or FacetGrid.
    """
    if ax is None:
        ax = plt.gca()

    # Standardize data for consistent ellipses
    scaler = MinMaxScaler()
    scaled_data = scaler.fit_transform(data[[x, y]])
    x_vals, y_vals = scaled_data[:, 0], scaled_data[:, 1]

    # Compute covariance and eigen decomposition
    cov = np.cov(x_vals, y_vals)
    eigvals, eigvecs = np.linalg.eig(cov)

    # Normalize ellipse size (ensures all ellipses fit in a fixed-size box)
    max_eigenvalue = np.max(eigvals)
    width, height = max_size * (eigvals / max_eigenvalue)
    angle = np.degrees(np.arctan2(*eigvecs[:, 0][::-1]))

    # Draw ellipse at the center
    ellipse = Ellipse(
        xy=(0, 0), width=width, height=height,
        angle=angle, edgecolor="black", facecolor="gray", alpha=0.3
    )
    ax.add_patch(ellipse)

    # Fix axis limits so all ellipses are comparable
    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.set_xticks([])
    ax.set_yticks([])
    ax.set_frame_on(False)

    return ax  # Return modified axis

def smart_sns_plot(x, y, data, ax=None, **kwargs):
    """
    Automatically delegates to sns.scatterplot, sns.violinplot, or sns.heatmap 
    based on the data types of x and y.

    - Continuous vs. Continuous → sns.scatterplot
    - Continuous vs. Discrete → sns.violinplot
    - Discrete vs. Discrete → sns.heatmap
    """
    if ax is None:
        ax = plt.gca()

    # Determine data types
    x_dtype = data[x].dtype
    y_dtype = data[y].dtype
    is_x_cont = np.issubdtype(x_dtype, np.number)
    is_y_cont = np.issubdtype(y_dtype, np.number)

    if is_x_cont and is_y_cont:
        # Continuous vs. Continuous → Scatter Plot
        sns.scatterplot(x=x, y=y, data=data, ax=ax, **kwargs)
        
    elif is_x_cont and not is_y_cont:
        # Continuous vs. Discrete → Violin Plot
        sns.violinplot(x=y, y=x, data=data, ax=ax, **kwargs)
        
    elif not is_x_cont and is_y_cont:
        # Discrete vs. Continuous → Violin Plot (flipped)
        sns.violinplot(x=x, y=y, data=data, ax=ax, **kwargs)
        
    else:
        # Discrete vs. Discrete → Heatmap
        cross_tab = pd.crosstab(data[x], data[y])
        sns.heatmap(cross_tab, annot=True, fmt="d", cmap="Blues", ax=ax, cbar=False)

    return ax  # Return the modified axis

# Example Data
a = np.random.uniform(size=100)
b = np.random.uniform(size=100)
df = pd.DataFrame({
    'A': (a) * 100.0,
    'B': (b) * 100.0,
    'C': (a - b) - 100.0,    
    'D': (a + b) * 50.0 - 50.0,
    'E': np.random.choice(['Low', 'Medium', 'High'], 100),
    'F': np.random.choice(['Yes', 'No'], 100)
})

# Create PairGrid
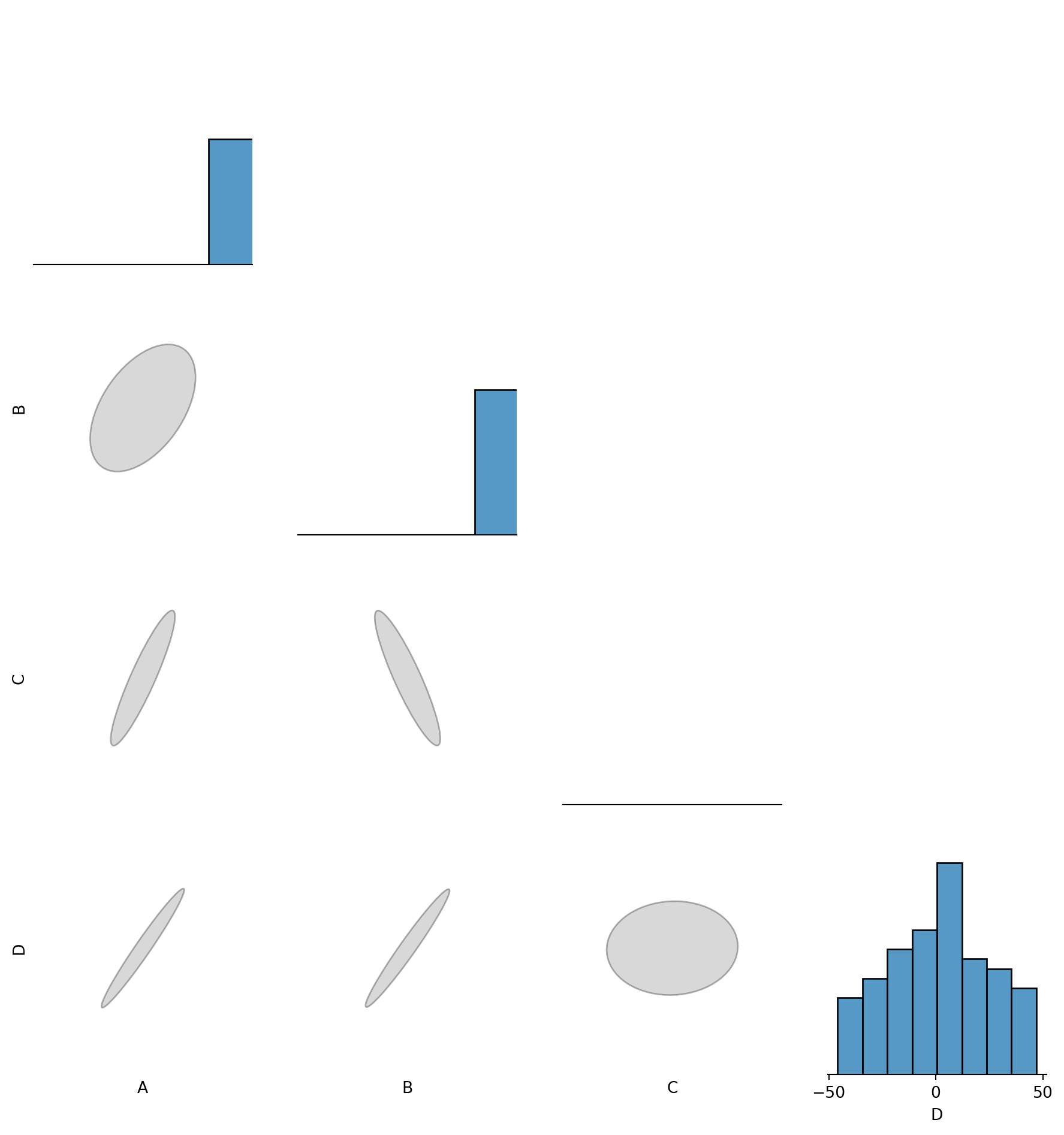
g = sns.PairGrid(df, diag_sharey=False)

# Upper Triangle: Use smart_sns_plot
g.map_upper(smart_sns_plot)

# Lower Triangle: Use sns_correlation_ellipse
g.map_lower(sns_correlation_ellipse)

# Diagonal: Histograms
g.map_diag(sns.histplot, kde=True, bins=20, color="lightblue")

plt.show()

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[6], line 103
    100 g = sns.PairGrid(df, diag_sharey=False)
    102 # Upper Triangle: Use smart_sns_plot
--> 103 g.map_upper(smart_sns_plot)
    105 # Lower Triangle: Use sns_correlation_ellipse
    106 g.map_lower(sns_correlation_ellipse)

File ~/work/notes/notes-islr-py/.venv/lib/python3.10/site-packages/seaborn/axisgrid.py:1410, in PairGrid.map_upper(self, func, **kwargs)
   1399 """Plot with a bivariate function on the upper diagonal subplots.
   1400 
   1401 Parameters
   (...)
   1407 
   1408 """
   1409 indices = zip(*np.triu_indices_from(self.axes, 1))
-> 1410 self._map_bivariate(func, indices, **kwargs)
   1411 return self

File ~/work/notes/notes-islr-py/.venv/lib/python3.10/site-packages/seaborn/axisgrid.py:1574, in PairGrid._map_bivariate(self, func, indices, **kwargs)
   1572     if ax is None:  # i.e. we are in corner mode
   1573         continue
-> 1574     self._plot_bivariate(x_var, y_var, ax, func, **kws)
   1575 self._add_axis_labels()
   1577 if "hue" in signature(func).parameters:

File ~/work/notes/notes-islr-py/.venv/lib/python3.10/site-packages/seaborn/axisgrid.py:1583, in PairGrid._plot_bivariate(self, x_var, y_var, ax, func, **kwargs)
   1581 """Draw a bivariate plot on the specified axes."""
   1582 if "hue" not in signature(func).parameters:
-> 1583     self._plot_bivariate_iter_hue(x_var, y_var, ax, func, **kwargs)
   1584     return
   1586 kwargs = kwargs.copy()

File ~/work/notes/notes-islr-py/.venv/lib/python3.10/site-packages/seaborn/axisgrid.py:1659, in PairGrid._plot_bivariate_iter_hue(self, x_var, y_var, ax, func, **kwargs)
   1657         func(x=x, y=y, **kws)
   1658     else:
-> 1659         func(x, y, **kws)
   1661 self._update_legend_data(ax)

TypeError: smart_sns_plot() missing 1 required positional argument: 'data'